Суть расчета сводится к определению деформаций, которые может иметь проектируемый элемент в процессе его эксплуатации и сравнение их с предельно допустимыми значениями параметра, обусловленными технологическими, конструктивными, эстетическими и психологическими требованиями.
Предельные значения определяются по СНиП 2.01.07-85* и нормативными документам на отдельные виды конструкции. Для любых конструкций предельный прогиб должен быть не более (1/150)l (пролета) для балок или (1/75)l ( для консолей).
Основное условие расчета:
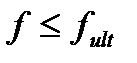 (5.31)
(5.31)
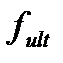 - предельный допустимый прогиб
- предельный допустимый прогиб
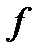 - прогиб элемента обусловленный деформацией изгиба и сдвига (сдвиг учитывается при гибкости элемента
- прогиб элемента обусловленный деформацией изгиба и сдвига (сдвиг учитывается при гибкости элемента 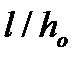 <10) от продолжительного и непродолжительного действия постоянных и временных нагрузок.
<10) от продолжительного и непродолжительного действия постоянных и временных нагрузок.
Прогиб 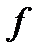 определяется в зависимости от кривизны элемента по общим правилам строительной механики. Выполнение условия (5.31) гарантирует конструкцию от чрезмерных деформаций, при которых ее эксплуатация затруднена или невозможна, даже при условии, что прочность и трещиностойкость обеспечена.
определяется в зависимости от кривизны элемента по общим правилам строительной механики. Выполнение условия (5.31) гарантирует конструкцию от чрезмерных деформаций, при которых ее эксплуатация затруднена или невозможна, даже при условии, что прочность и трещиностойкость обеспечена.
Поскольку предельные деформации должны быть ограничены, то к моменту их достижения несущая способность как правило не исчерпана в большинстве элементов, поэтому расчет введут по нормативным нагрузкам при 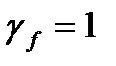 . Так как жесткость сечений до и после образования трещин значительно отличается, то существенно отличаются и методы расчета элементов работающих с трещинами в растянутой зоне или без них.
. Так как жесткость сечений до и после образования трещин значительно отличается, то существенно отличаются и методы расчета элементов работающих с трещинами в растянутой зоне или без них.
В ПН элементах из-за позднего образования трещин наблюдается значительно более высокая изгибная жесткость по сравнению с аналогами без НП. Однако при образовании трещин предварительное напряжения (обжатие) полностью гасится и дальнейший прирост прогибов у ПН элемента будут отличаться от прироста прогибов в элементах без ПН, только при наличии у первых (у ПН элементов) высокого усилия предварительного обжатия, создающего момент. Этот момент увеличивает долю упругих обратимых прогибов.
Прогибы элементов, у которых в стадии эксплуатации не образуются трещины в растянутой зоне близки к прогибам элементов из упругих материалов.
Как показывает опыт проектирования прогиб для них может быть определен по формулам сопротивления упругих материалов, т.е. в предположении упругой работы бетона как сжатой, так и растянутой зон.
Для элементов, работающих с трещинами в растянутой зоне, прогибы так же могут определяться по формулам для упругих материалов, но с учетом пластической работы сжатого бетона и растянутой арматуры (учет пластических деформаций сжатого бетона и растянутых бетона и арматуры) путем определения фактической кривизны, причем эта кривизна должна определятся от начального состояния элемента, т.е. с момента передачи усилия 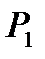 на бетон.
на бетон.
Прогиб элемента
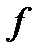 определяется:
определяется:
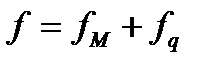 (5.32)
(5.32)
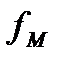 прогиб элемента, обусловленный деформацией изгиба. В общем случае он определяется:
прогиб элемента, обусловленный деформацией изгиба. В общем случае он определяется:
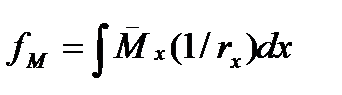 (5.33)
(5.33)
Mx - изгибаемый момент в сечении Х вычисленный от единичной силы 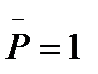 приложенной в сечении, где вычисляется прогиб.
приложенной в сечении, где вычисляется прогиб.
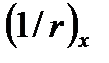 - полная кривизна в сечении Х от внешней нагрузки при которой определяется прогиб
- полная кривизна в сечении Х от внешней нагрузки при которой определяется прогиб 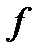 .
.
Обычно элемент делится на n участков (n 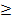 6 и четное число) и кривизна определяются на границах этих участков (с учетом наличия или отсутствии трещин в пределах участка). Распределение кривизны в пределах в пределах участка принимается линейно.
6 и четное число) и кривизна определяются на границах этих участков (с учетом наличия или отсутствии трещин в пределах участка). Распределение кривизны в пределах в пределах участка принимается линейно.
Для середины пролета:
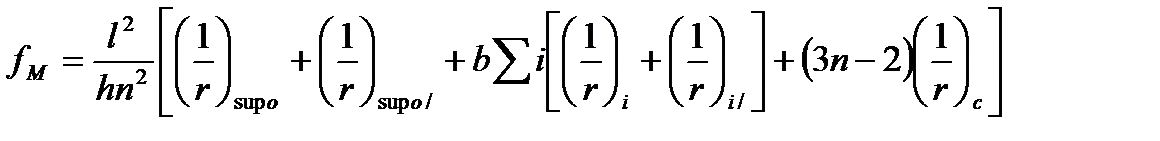 (5.34)
(5.34)
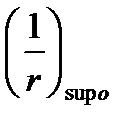 и
и 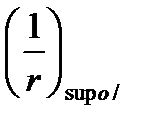 - кривизна на левой и правой опоре.
- кривизна на левой и правой опоре.
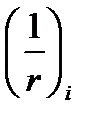 - кривизна на границах участков и при
- кривизна на границах участков и при 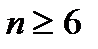 .
. 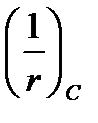 - кривизна в середине
- кривизна в середине 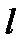
Даже такое упрощение деформации фактической кривизны делает решение громоздким, поэтому для практических расчетов элементов с постоянным по длине сечением применяют некую кривизну 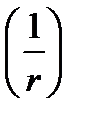 вычисляемую для наиболее напряженного по длине участка и считают, что эта кривизна меняется пропорционально моменту в пределах участка. То есть жесткость вычисляется для самого напряженного сечения и считается неизменной, хотя в реальности она зависит от нагрузки и НДС участка.
вычисляемую для наиболее напряженного по длине участка и считают, что эта кривизна меняется пропорционально моменту в пределах участка. То есть жесткость вычисляется для самого напряженного сечения и считается неизменной, хотя в реальности она зависит от нагрузки и НДС участка.
Для свободно опертых балок и консолей при неизменных размерах сечения (h и b=const) допускается определять прогиб по формуле:
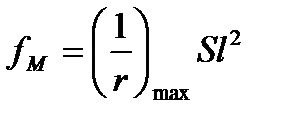 (5.35)
(5.35)
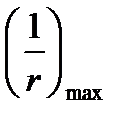 - кривизна сечения с max моментом М,
- кривизна сечения с max моментом М,
S – коэффициент зависящий от операния и загружения элемента.
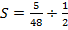 определяется по таблице 4.3 СП 52-102-2003г.
определяется по таблице 4.3 СП 52-102-2003г.
Если при прогибе 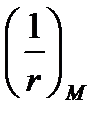 по формуле (5.35) не выполняется условие (5.31), то прогиб может быть уточнен путем учета фактической кривизны участков, где трещины не образуются (т.е. участков с фактически большей жесткостью) по формуле (5.34).
по формуле (5.35) не выполняется условие (5.31), то прогиб может быть уточнен путем учета фактической кривизны участков, где трещины не образуются (т.е. участков с фактически большей жесткостью) по формуле (5.34).
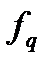 - прогиб, обусловленный деформацией сдвига. Это величина учитывает влияние перерезывающей силы Q на прогиб f
- прогиб, обусловленный деформацией сдвига. Это величина учитывает влияние перерезывающей силы Q на прогиб f
При гибкости элемента l / h≥10 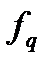 =0. В противном случае для жестких элементов.
=0. В противном случае для жестких элементов.
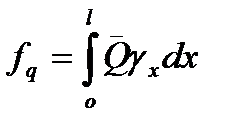 (5.36)
(5.36)
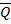 - перерезывающая сила в сечении х от единичной силы
- перерезывающая сила в сечении х от единичной силы 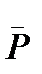 =1 приложеной в сечении, где определяется прогиб
=1 приложеной в сечении, где определяется прогиб 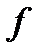 .
.
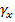 - угол сдвига элемента от внешней нагрузки в сечении х, от внешней нагрузки.
- угол сдвига элемента от внешней нагрузки в сечении х, от внешней нагрузки.
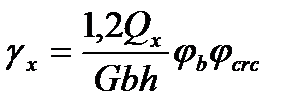 (5.37)
(5.37)
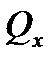 - поперечная сила в сечении х от внешней нагрузки.
- поперечная сила в сечении х от внешней нагрузки.
G - модуль сдвига
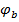 - коэффициент учитывающий ползучесть бетона; при непродолжительном действии нагрузки
- коэффициент учитывающий ползучесть бетона; при непродолжительном действии нагрузки 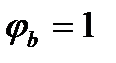 , при продолжительном
, при продолжительном 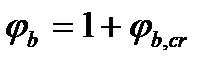 .
.
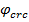 - коэффициент, учитывающий влияние наличия трещин на деформацию сдвига:
- коэффициент, учитывающий влияние наличия трещин на деформацию сдвига:
а) если нет нормальных и наклонных трещин, т.е. выполняется условие (5.1 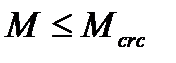 ) и (4.49
) и (4.49 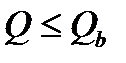 ), то
), то 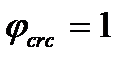
б) есть только наклонная трещина, т.е. условие (4.49) не выполняется, при выполнении условия (5.1), то 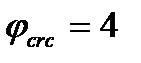 .
.
в) если есть нормальные трещины условие (5.1) не выполняется, а условие (4.49) может выполнятся, может и нет, то
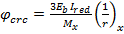 (5.38)
(5.38)
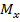 ;
; 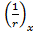 - момент и кривизна сечения от фактической нагрузки;
- момент и кривизна сечения от фактической нагрузки; 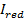 при
при 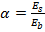
Дата: 2018-12-28, просмотров: 486.