К таким элементам относятся конструкции, к которым не предъявляются требования по непроницаемости (допускается образование трещин) и для которых не выполнено условие (5.1), т.е. образуются трещины. Расчет ведется по модели для второй стадии НДС.

Для этого состояния, то есть к моменту образования первых трещин обжатие элемента полностью гасится, поэтому относительная кривизна от выгиба элемента усилием 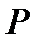  с моментом  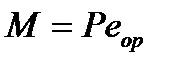не влияет на кривизну и не учитывается. А необратимая кривизна от выгиба вызванного усадкой и ползучестью 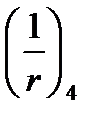от силы 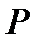, учитывается так же как для элементов без трещин по формуле (5.40) 

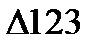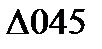 и - подобны, тогда 3-2 : 4-5 относятся как 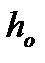: r , то есть кривизна на элемент с трещино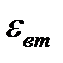й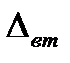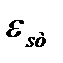.  и ,  и 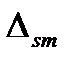- это средние относительные и средние абсолютные деформации сжатой зоны и растянутой арматуры. Тогда 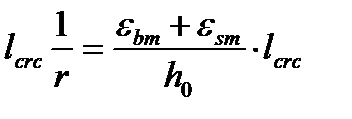. Сократив получим уравнение изогнутой оси:

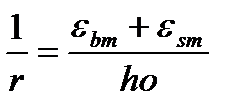Кривизна есть отношение суммы средних деформаций крайнего сжатого волокна бетона и растянутой арматуры к рабочей высоте .

Если бы элемент работал упруго, то кривизна 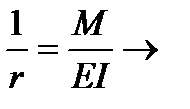 Следовательно задача сводится к определению связи между двумя этими выражениями, чтобы выражения для упругих материалов могли быть применены к бетону.

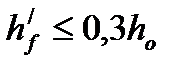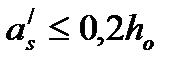Для элементов прямоугольного сечения, а так же тавровых и двутавровых сеченый при   и  кривизну можно определить:

Для элементов с ПН: 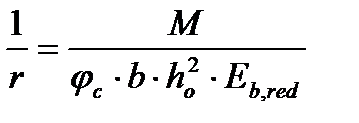                       (5.46)

Для элементов без ПН: 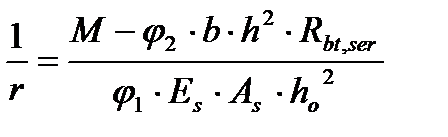           (5.47)

Для формулы (5.46) 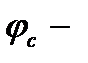определяется по таблице 4.5 СП 51-102- 2003 в зависимости от армирования ( 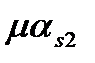), геометрии сечения ( 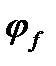, есть полки или нет и т.д.) и НДС ( ).

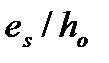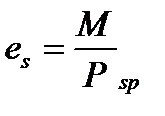(5.18)

            (5.48)

Где 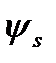определяется по формуле (5.27).

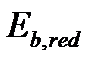 - приведенный модуль деформации.

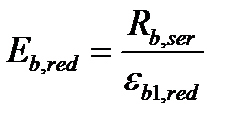                          (5.49)

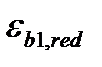- приведенная деформация сжатого бетона в пластичном состоянии.

При продолжительном действии нагрузки: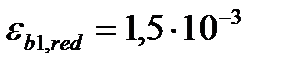      

При непродолжительном действии нагрузки: 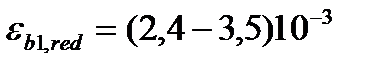 (при W=75-40% - 2,8*10^-3)

В формуле (5.47) 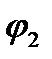  и 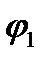 - определяются по формулам (4.5) (4.6) СП 51-101- 2003 в зависимости от наличия или отсутствия, а также от соотношения сжатых и растянутых полок и от армирования  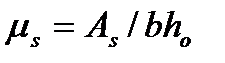сечения.

Полная кривизна элемента с трещиной в растянутой зоне:

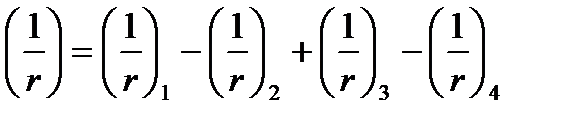                          (5.50)

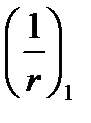- кривизна по формулам (5.46) и (5.47) от непродолжительного действия полной нагрузки. ,

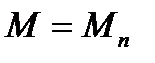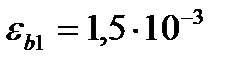
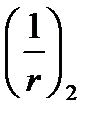- непродолжительное действие постоянных и длительных нагрузок ,

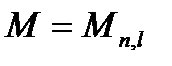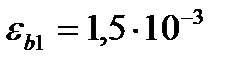
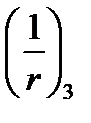- продолжительное действие постоянных и длительных нагрузок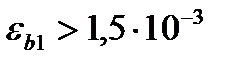

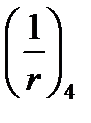-кривизна от выгиба в результате действия усадки и ползучести (по формуле 5.40)

После передачи усилия 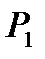 c упоров на бетон в элементе создается обжатие силой  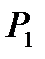и с изгибом при 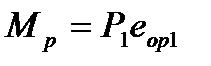, вызывающий начальный выгиб и кривизну 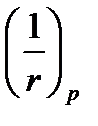, обратную по знаку кривизне от будущих эксплуатационных нагрузок (точка 1).

На полную кривизну это слагаемое не оказывает влияния, так как при наступлении стадии II НДС (именно по ней и введется расчет) обжатие силой P полностью гасится и образуются трещины, то есть 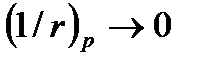(компенсируется внешней нагрузкой). Затем натекают потери от ползучести и усадки, вызывая дополнительный выгиб и кривизну 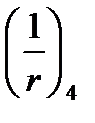, того же знака что и 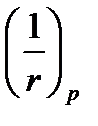(линия 1-2).

Обжатие снижается до P, а момент 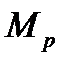 до 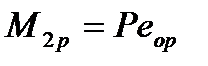. Кривизна увеличена на  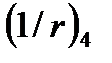по абсолютному значению (точка 2). Затем элемент монтируется на проектное место и прикладывается эксплуатационная нагрузка. С ростом нагрузки внешней момент  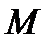увеличивается до  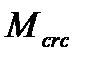(точка 3) - момент при котором образуются трещины, при котором P полностью гасится. В процессе этого кривизна меняет знак (линия 2-3).

При кратковременном действии нагрузки, вызывающей полный расчетный момент 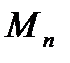, кривизна увеличивается до 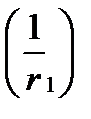(точка 7). Такая же полная кривизна была бы у балки без ПН.

Элементы с ПН: 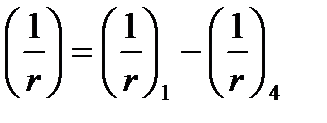                      Элемент без ПН: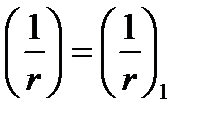

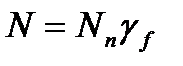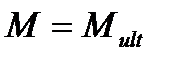Если нагрузка будет увеличиваться до разрушающей при нагрузке  и , кривизна будет меняться по линии 7-8- линия разрушения.

Если после приложения полной эксплуатационной нагрузки 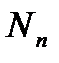 с моментом  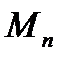кратковременная часть 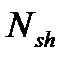ее с моментом  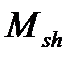будет снята (как это и бывает в реальности) и на конструкции остается только длительная часть нагрузки 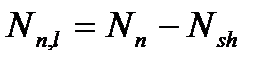, то кривизна уменьшается до точки 4 , то есть кратковременное действие длительной нагрузки  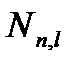вызывает кривизну .

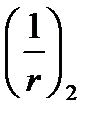Длительное действие длительной нагрузки вызывает 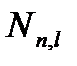 вызывает прирост кривизны по линии 4-5 - 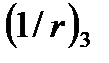.Кратковременное приложение  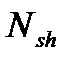- вызывает кривизну по линии 5-6, идентичной линии 4-7. Таким образом, кривизна от внешней нагрузки – это сумма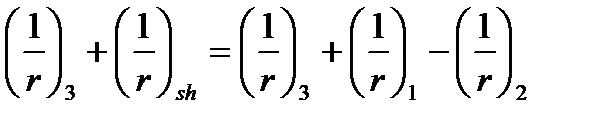   

А полная кривизна с учетом потерь ползучести и усадки отражена в формуле (5.50)

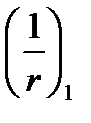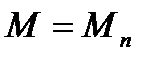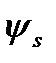 - вычисляется по формуле (5.46) или (5.47) при  и при  и 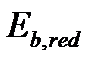 - отвечающих непродолжительному действию нагрузки.

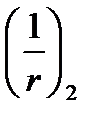- вычисляется так же, но при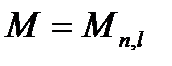

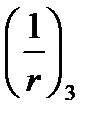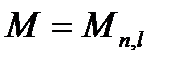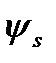- вычисляется по формуле (5.46) или (5.47) при  и при  и 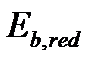 - отвечающих длительному действию нагрузки и деформированию.

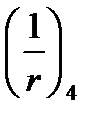- определяется по формуле (5.40) и все относящее к этому слагаемому для элементов без трещин, справедливо и для элементов с трещиной в растянутой зоне.

Элементы без ПН:

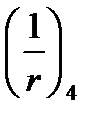=0, а остальные слагаемые определяются так же как и для элементов с ПН, таким образом положительные влияние ПН на деформацию элементов выражается слагаемым 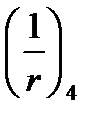, то есть начальным выгибом и повышенной жесткостью по сравнению с элементами без ПН (последнее отражено в коэффициенте ).

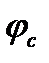Кривизна 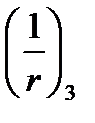 от длительной части нагрузки может в несколько раз превосходить кривизну от кратковременной части нагрузки  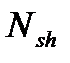- 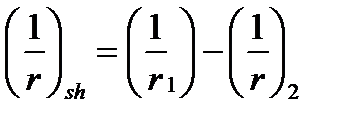. Благодаря которым деформация ползучести при действии экстремальной нагрузки, причем чем выше напряжение в сжатой зоне бетона, тем эта разница будет существенней.