5.3.1 Расчет на образование трещин внецентренно сжатых и растянутых элементов.
Как и в изгибаемых элементах трещины не образуются при выполнении условия (5.1), т.е 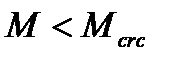 .
.
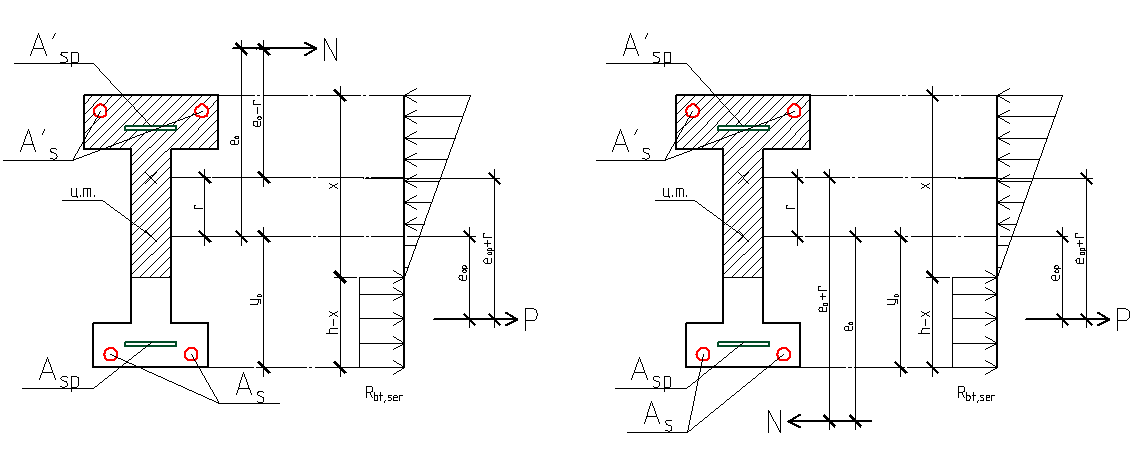
Рис.117
Левая часть уравнения в стадии эксплуатации определяется:
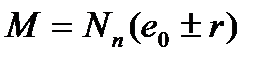 (5.51)
(5.51)
где 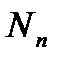 сжимающее либо растягивающее усилие в сечении.
сжимающее либо растягивающее усилие в сечении.
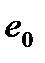 - эксцентриситет этого усилия относительно центра тяжести сечения.
- эксцентриситет этого усилия относительно центра тяжести сечения.
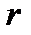 - расстояние до ядровой точки 1, наиболее удаленной от растянутой зоны. Знак «+» применяется при растягивающей силе
- расстояние до ядровой точки 1, наиболее удаленной от растянутой зоны. Знак «+» применяется при растягивающей силе 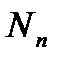 , «-« при сжимающей силе
, «-« при сжимающей силе 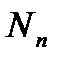
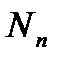 -усилие от нормативной нагрузки.
-усилие от нормативной нагрузки. 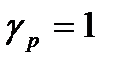
Правая часть условия (5.1) принимается как и для изгибаемых элементов (5.2)
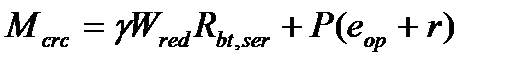 (5.2)
(5.2)
Учет неупругих деформаций производится коэф. 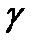 (см. п. 5.1.1)
(см. п. 5.1.1)
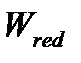 определяется как для упругого тела.
определяется как для упругого тела.
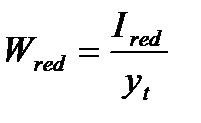 (5.52)
(5.52)
где 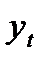 –расстояние наиболее растянутого волокна до ц.т .
–расстояние наиболее растянутого волокна до ц.т .
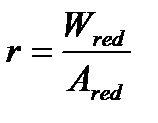 (5.53)
(5.53)
При 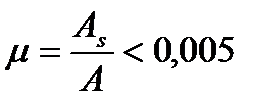 влияние арматуры можно не учитывать, т.е
влияние арматуры можно не учитывать, т.е 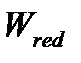 ,
, 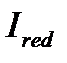 ,
, 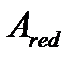 определяются только по бетону при
определяются только по бетону при 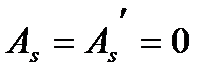 .
.
Т.е по стадии изготовления аналогичен расчету изгибаемых элементов (п.п 5.1.1. Б), т.к определяется только внешними усилиями от соответствующего веса элемента.
Для элементов без ПН применяют те же формулы при 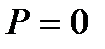 .
.
5.3.2 Расчет по образованию трещин центрально растянутых элементов.
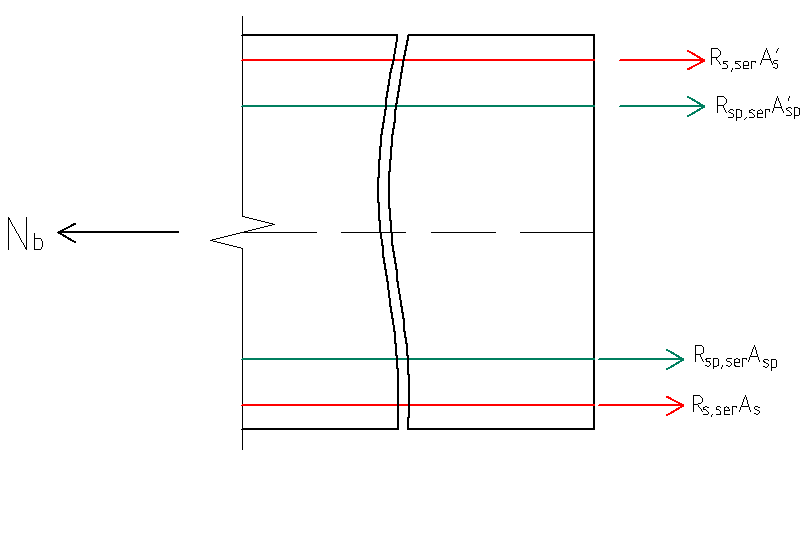 Трещины не образуются при выполнении условия полученного из уравнения равновесия всех сил на продольную ось (т.к
Трещины не образуются при выполнении условия полученного из уравнения равновесия всех сил на продольную ось (т.к 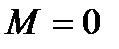 )
)
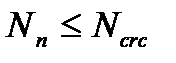 (5.54)
(5.54)
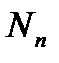 - растягивающее усилие от нормативной нагрузки.
- растягивающее усилие от нормативной нагрузки.
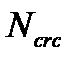 - усилие воспринимаемое сечением перед образованием трещин.
- усилие воспринимаемое сечением перед образованием трещин.
Рис.118
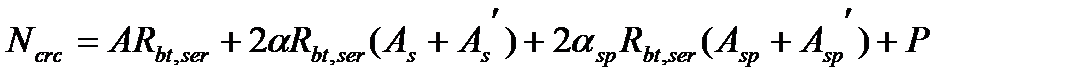 (5.55)
(5.55)
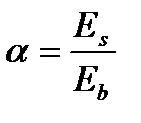 ;
; 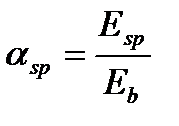 ;
; 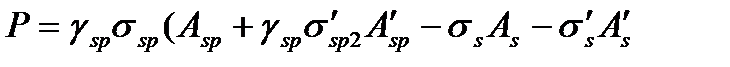 -усилие (5.56)
-усилие (5.56)
Предварительного обжатия с учетом всех потерь 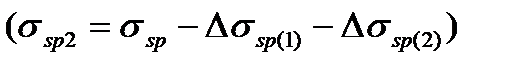 и коэф. точности натяжения
и коэф. точности натяжения 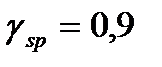
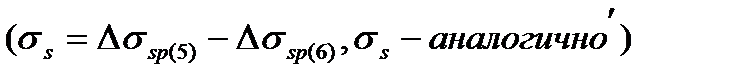
При отсутствие ПН 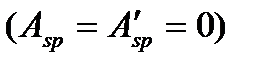
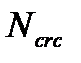 определяют:
определяют:
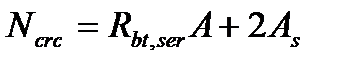 (5.57)
(5.57)
Где 2- напряжение в кН/см2 в арматуре перед образованием трещин (т.е 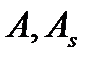 подставлять в см2, в
подставлять в см2, в 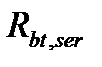 кН/см2)
кН/см2)
Расчет на раскрытие трещин.
Ширина раскрытия трещин в стадии изготовления производится так же как и для изгибаемых элементов (см. п.п 5.1.2) То же в стадии эксплуатации, т.е по формуле (5.14) для внецентренно сжатых и внецентренно и центрально растянутых элементов.
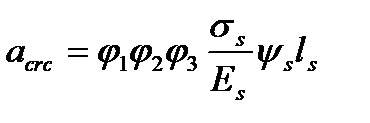 (5.14), с заменой
(5.14), с заменой 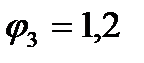 для растянутых и
для растянутых и 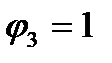 для сжатых элементов.
для сжатых элементов.
Для определения напряжения в растянутой арматуре формулу (5.15) изменяют следующим образом.
Для центрально растянутых элементов: 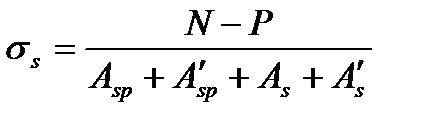 (5.58)
(5.58)
Где Р- усилие обжатия с учетом всех потерь и 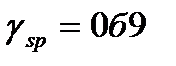 (коэффициент точности натяжения) по формуле (5.56).
(коэффициент точности натяжения) по формуле (5.56).
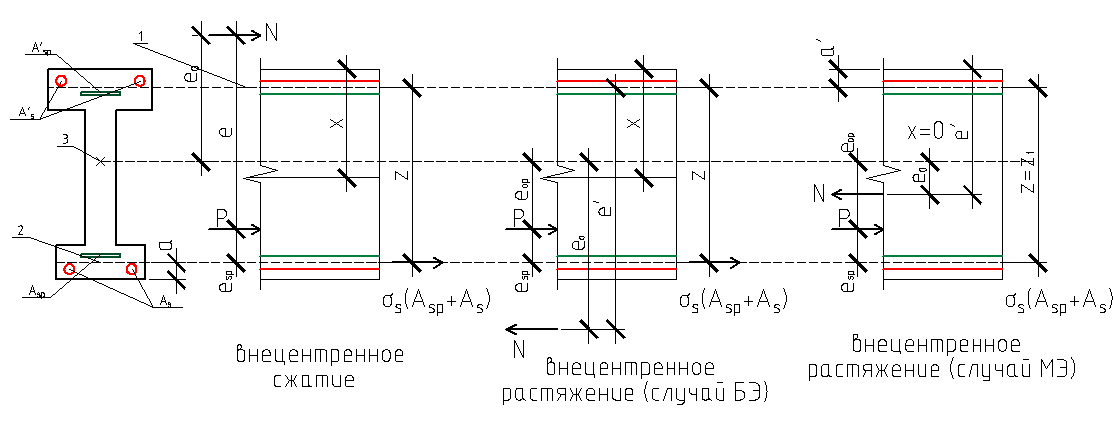
Рис.119
1- Точка равнодействующей усилий в сжатой зоне бетона.
2- Точка приложения равнодействующей усилий в растянутой арматуре 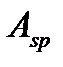 и
и 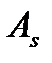 .
.
(для растяжения с МЭ - точка приложения равнодействующей в менее растянутой арматуре 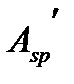 и
и 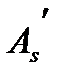 )
)
3- Центр тяжести приведенного сечения.
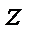 - плечо внутренней пары сил определяется по табл. 4.2 СП52-102-2003 (см п.5.1.2)
- плечо внутренней пары сил определяется по табл. 4.2 СП52-102-2003 (см п.5.1.2)
Для внецентренно растянутых элементов по случаю 2 (МЭ) 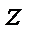 :
: 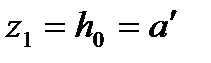
Получим выражение для 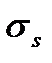 из уравнения равновесия моментов точки 1.
из уравнения равновесия моментов точки 1.
Внецентренно сжатые элементы: 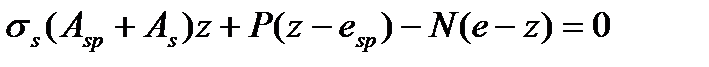
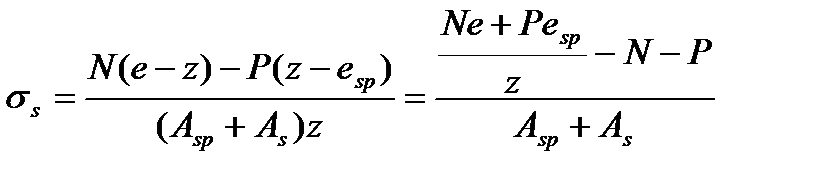 (5.59)
(5.59)
Эксцентриситет приложения 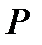 относительно центра тяжести арматуры
относительно центра тяжести арматуры 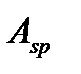 и
и 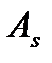 определяется при известном
определяется при известном 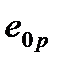 определенном по формуле (3.26);
определенном по формуле (3.26); 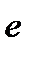 расстояние от точки приложения силы
расстояние от точки приложения силы 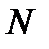 до центра тяжести арматуры
до центра тяжести арматуры 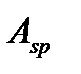 и
и 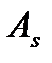 .
.
Внецентренно растянутые элементы по случаю 1 (БЭ). Уравнение моментов:
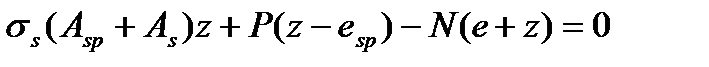
Внецентренно растянутые элементы по случаю 2 (МЭ)
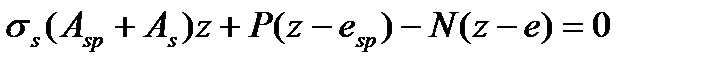
Тогда для внецентренно растянутых элементов получим: 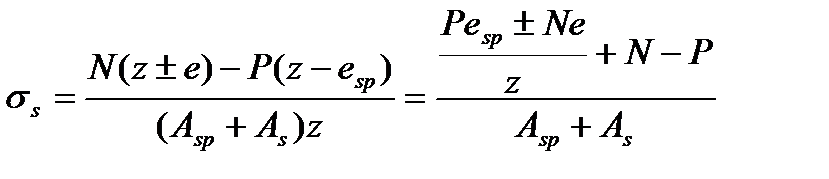
Где знак «+» для случая БЭ и знак «-» для случая малых эксцентриситетов при 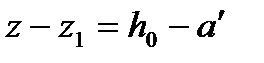 . При совпадении точки приложения
. При совпадении точки приложения 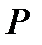 и центра тяжести арматуры
и центра тяжести арматуры 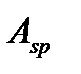 и
и 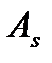 ,
,
т.е 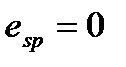 при
при 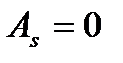 и
и 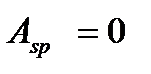 . Случай внецентренного растяжения и сжатия должен быть определен:
. Случай внецентренного растяжения и сжатия должен быть определен: 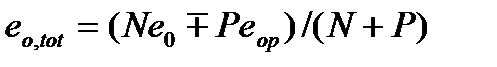 (5.61) («+»-сжатие)
(5.61) («+»-сжатие)
при 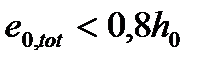 -случай МЭ.
-случай МЭ.
Для элементов из ПН 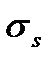 можно вычислять по формулам 5.52-5.60 при
можно вычислять по формулам 5.52-5.60 при 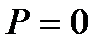 , а также сечений прямоугольной формы.
, а также сечений прямоугольной формы.
при 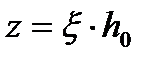
Для внецентренно растянутых: а) при 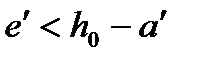 (расположение между арматурой
(расположение между арматурой 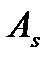 и
и 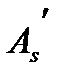 -случай МЭ)
-случай МЭ)
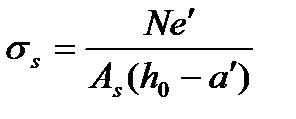 (5.62)
(5.62)
Б) при 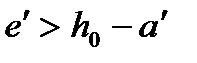 и при
и при 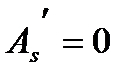
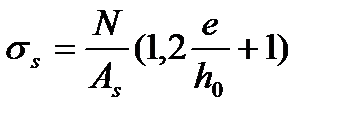 (5.63)
(5.63)
В) при 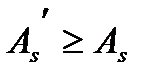 вне зависимости от
вне зависимости от 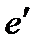 .
.
Г) при 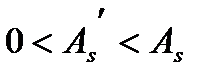 по линейной интерполяции между значениями по (5.62) и (5.63)
по линейной интерполяции между значениями по (5.62) и (5.63)
Для внецентренно сжатых элементов: 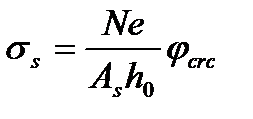 (5.63)
(5.63)
Где 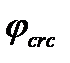 по табл. 4.2 СП52-101-2003
по табл. 4.2 СП52-101-2003
При определении 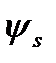 формула (5.27) вычисляется
формула (5.27) вычисляется 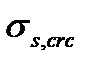 при
при
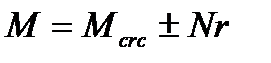 (5.64), где
(5.64), где 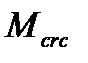 по формуле (5.2)
по формуле (5.2)
Знак «+»- при сжатии; «-»- при растяжении.
При этом 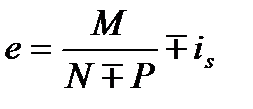 –от
–от 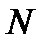 до арматуры
до арматуры 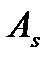 и
и 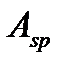 .
.
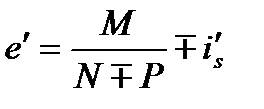 -до арматуры
-до арматуры 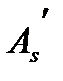 и
и 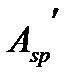 («+»-сжатие; «-»-растяжение) Во всех формула принимают
(«+»-сжатие; «-»-растяжение) Во всех формула принимают 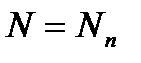
Ширину раскрытия трещин принимают по формулам 5.29 и 5.30
При определении 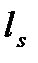 вычисляется
вычисляется 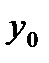 по формуле (вместо 5.25)
по формуле (вместо 5.25)
(5.65) 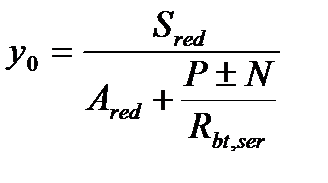 ,где
,где 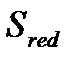 –статический момент относительно нижней грани.
–статический момент относительно нижней грани.
Дата: 2018-12-28, просмотров: 423.