(ВЫБОРОК БОЛЬШОГО ОБЬЕМА)
Первым шагом при обработке выборок большого объема является построение по исправленным результатам измерений 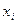 , где i = 1, 2,...,
, где i = 1, 2,..., 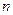 , вариационного ряда (упорядоченной выборки). В вариационном ряду результаты измерений (или их отклонения от среднего арифметического) располагают в порядке возрастания от
, вариационного ряда (упорядоченной выборки). В вариационном ряду результаты измерений (или их отклонения от среднего арифметического) располагают в порядке возрастания от 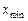 до
до 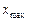 . Далее этот ряд разбивается на оптимальное число
. Далее этот ряд разбивается на оптимальное число 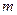 , как правило, одинаковых интервалов группирования длиной
, как правило, одинаковых интервалов группирования длиной 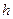 = (
= ( 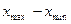 ) /
) / 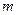 .
.
Оптимальное число интервалов группирования рассчитывается из выражения 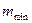 = 0,55
= 0,55 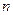 0,4 и
0,4 и 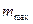 = 1,25
= 1,25 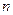 0,4, которые получены для наиболее часто встречающихся на практике распределении с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа.
0,4, которые получены для наиболее часто встречающихся на практике распределении с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа.
Искомое значение 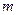 должно находится в пределах от
должно находится в пределах от 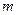 min до
min до 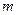 max, быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается. В случае, если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования
max, быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается. В случае, если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования 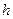 всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.
всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.
Далее определяют интервалы группирования экспериментальных данных в виде  D1= (
D1= ( 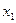 ,
, 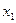 +
+ 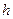 ); D2= (
); D2= ( 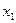 +
+ 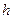 ,
, 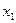 +2
+2 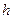 );....; Dm= (
);....; Dm= ( 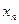 -
- 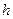 ;
; 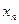 ), и подсчитывают число попаданий
), и подсчитывают число попаданий 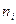 (частоты) результатов измерений в каждый интервал группирования. Сумма
(частоты) результатов измерений в каждый интервал группирования. Сумма 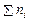 частот должна равняться объему выборки
частот должна равняться объему выборки 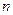 . По полученным значениям рассчитывают вероятности попадания результатов измерений (
. По полученным значениям рассчитывают вероятности попадания результатов измерений (  -относительные частоты или частости) в каждый из интервалов группирования по формуле:
-относительные частоты или частости) в каждый из интервалов группирования по формуле:
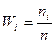 ,
,
где 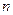 - объем выборки.
- объем выборки.
Проведенные расчеты позволяют построить гистограмму, полигон и кумулятивную кривую. Для построения гистограммы по оси результатов наблюдений Х откладываются интервалы Dk в порядке возрастания номеров и на каждом интервале строится прямоугольник высотой 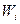 /
/ 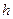 (плотность относительной частоты). При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой — графику плотности распределения вероятности. Следует отметить, что в ряде случаев производят расчетное симметрирование гистограммы.
(плотность относительной частоты). При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой — графику плотности распределения вероятности. Следует отметить, что в ряде случаев производят расчетное симметрирование гистограммы.
Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы. Он более наглядно, чем гистограмма, отражает форму кривой распределения. За пределами гистограммы справа и слева остаются пустые интервалы, в которых точки, соответствующие их серединам, лежат на оси абсцисс.
Эти точки при построении полигона соединяют между собой отрезками прямых линий. В результате совместно с осью Х образуется замкнутая фигура, площадь которой в соответствии с правилом нормирования должна быть равна единице (или числу наблюдений при использовании частостей).
Далее определяются характеристики выборки 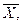 СКО по формулам:
СКО по формулам:
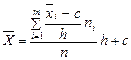 ;
; 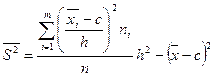 ;
;
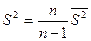 ;
; 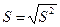 ,
,
где 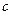 - «ложный нуль», используемый для упрощения расчетов, принимается равным среднему значению интервала, имеющего максимальную частоту.
- «ложный нуль», используемый для упрощения расчетов, принимается равным среднему значению интервала, имеющего максимальную частоту.
Идентификация закона распределения результатов измерений
При числе наблюдений n > 50 для идентификации закона распределения используется критерий Пирсона (хи-квадрат) или критерий Мизеса-Смирнова (w2). При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207-76.
При n<15 принадлежность экспериментального распределения к нормальному не проверяется.
Закон нормального распределения имеет фундаментальное значение для теории обработки результатов измерений. Центральная предельная теорема утверждает, что закон распределения суммарной погрешности измерений близок к нормальному (усеченному) распределению всякий раз, когда результаты наблюдений формируются под влиянием большого числа независимо действующих случайных составляющих, каждая из которых оказывает лишь незначительное действие по сравнению с суммарной погрешностью. Кроме того, нормальный закон позволяет вести расчеты даже тогда, когда действительный закон неизвестен, потому что нормальный закон дает чаще увеличенный, чем уменьшенный доверительный интервал.
Наибольшее распространение в практике получил критерий Пирсона. Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе распределения, совпадение с которым определяется. Использование критерия Пирсона возможно при большом числе измерений (n>50) и заключается в вычислении величины c2 (хи-квадрат):
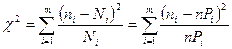 ,
,
где ni, Ni — экспериментальные и теоретические значения частот в i-м интервале разбиения; m — число интервалов разбиения; Р i — значения вероятностей в том же интервале разбиения, соответствующие выбранной модели распределения; 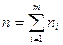 при n®¥ случайная величина c2 имеет распределение Пирсона с числом степеней свободы n= m -1- r, где r — число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Для нормального закона распределения r = 2, так как закон однозначно характеризуется указанием двух его параметров — математического ожидания и СКО.
при n®¥ случайная величина c2 имеет распределение Пирсона с числом степеней свободы n= m -1- r, где r — число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Для нормального закона распределения r = 2, так как закон однозначно характеризуется указанием двух его параметров — математического ожидания и СКО.
Если бы выбранная модель в центрах всех m столбцов совпадала с экспериментальными данными, то все m разностей (ni – Ni) были бы равны нулю, а следовательно, и значение критерия c2 также было бы равно нулю. Таким образом, c2 есть мера суммарного отклонения между моделью и экспериментальным распределением.
Критерий c2 не инвариантен к числу столбцов и существенно возрастает с увеличением их числа. Поэтому для использования его при разном числе столбцов составлены таблицы квантилей распределения c2, входом в которые служит так называемое число степеней свободы n= m -1- r. Чтобы совместить модель, соответствующую нормальному закону, с гистограммой, необходимо совместить координату центра, а для того, чтобы ширина модели соответствовала ширине гистограммы, ее нужно задать как r = 2 и n = m-3. Часть квантилей распределения c 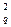 приведена в табл.5.1.
приведена в табл.5.1.
Если вычисленная по опытным данным мера расхождения c2 меньше определенного из таблицы значения c 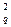 , то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. она не противоречит опытным данным.
, то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. она не противоречит опытным данным.
Таблица 5.1 Значения c 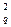 , при различном уровне значимости
, при различном уровне значимости
| n
| c Xq при уровне значимости q, равном
| ||||||||
| 0,99 | 0,95 | 0,9 | 0,8 | 0,5 | 0,2 | 0,1 | 0,05 | 0,02 | |
| 2 | 0,02 | 0,1 | 0,21 | 0,45 | 1,39 | 3,22 | 4,61 | 5,99 | 7,82 |
| 4 | 0,3 | 0,71 | 1,06 | 1,65 | 3,36 | 5,99 | 7,78 | 9,49 | 11,67 |
| 6 | 0,87 | 1,63 | 2,20 | 3,07 | 5,35 | 8,56 | 10,65 | 12,59 | 15,03 |
| 8 | 1,65 | 2,73 | 3,49 | 4,59 | 7,34 | 11,03 | 13,36 | 15,51 | 18,17 |
| 10 | 2,56 | 3,94 | 4,87 | 6,18 | 9,34 | 13,44 | 15,99 | 18,31 | 21,16 |
| 12 | 3,57 | 5,23 | 6,30 | 7,81 | 11,34 | 15,81 | 18,55 | 21,03 | 24,05 |
| 14 | 4,66 | 6,57 | 7,79 | 9,47 | 13,34 | 18,15 | 21,06 | 23,69 | 26,87 |
| 16 | 5,81 | 7,96 | 9,31 | 11,2 | 15,34 | 20,46 | 23,54 | 26,3 | 29,63 |
| 20 | 8,26 | 10,85 | 12,44 | 14,58 | 19,34 | 25,04 | 28,41 | 31,41 | 35,02 |
| 25 | 11,52 | 14,61 | 16,47 | 18,94 | 24,34 | 30,68 | 34,38 | 37,65 | 41,57 |
| 30 | 14,95 | 18,46 | 20,60 | 23,36 | 29,34 | 36,25 | 40,26 | 43,77 | 47,96 |
Если же c2 расчетное превышает c 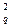 , то гипотеза отвергается как противоречащая опытным данным.
, то гипотеза отвергается как противоречащая опытным данным.
Методика определения соответствия экспериментального и принятого законов распределения заключается в следующем:
- определяют оценки среднего арифметического значения 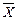 и СКО Sx;
и СКО Sx;
- группируют результаты многократных наблюдений по интервалам длиной h, число которых определяют так же, как и при построении гистограммы;
- для каждого интервала разбиения определяют число наблюдений ni, попавших в каждый интервал;
- вычисляют вероятность появления результатов в данном интервале, согласно принятой теоретической модели распределения.
Для этого сначала от реальных границ интервалов производят переход к нормированным значениям по формуле: 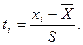
Затем подсчитывают вероятность 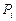 для каждого интервала по формуле:
для каждого интервала по формуле:
Pi = Ф( ti +1 ) – Ф( ti ), где Ф( ti ) – значение функции Лапласа на границе i-го интервала, определяемое по таблицам распределения Лапласа ( см. Приложение 2).
Для крайних значений выборки 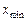 и
и 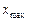 значения функции Лапласа определены и согласно ее свойствам равны:
значения функции Лапласа определены и согласно ее свойствам равны: 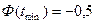 ;
; 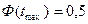 ;
;
- по формуле 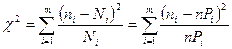 определяют показатель разности частот c2;
определяют показатель разности частот c2;
- выбирают уровень значимости критерия q. Он должен быть небольшим, чтобы была мала вероятность совершить ошибку первого рода.
Для удобства вычислений все расчеты сводятся в таблицу:
| Интервалы | ni | Pi | nPi | (ni-nPi)2 | (ni-nPi)2 /( nPi ) |
По уровню значимости и числу степеней свободы n по табл.4.1 находят границу критической области c 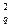 , такую, что вероятность Р{c2 > c
, такую, что вероятность Р{c2 > c 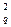 } = q. Вероятность того, что полученное значение c2 превышает c
} = q. Вероятность того, что полученное значение c2 превышает c 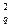 , равна уровню значимости q и мала. Поэтому, если оказывается, что c2 > c
, равна уровню значимости q и мала. Поэтому, если оказывается, что c2 > c 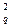 , то гипотеза о совпадении экспериментального и теоретического законов распределения отвергается. Если же c2 < c
, то гипотеза о совпадении экспериментального и теоретического законов распределения отвергается. Если же c2 < c 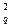 , то гипотеза принимается.
, то гипотеза принимается.
Чем меньше q, тем больше значение c 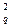 (при том же числе степеней свободы n), тем легче выполняется условие c2 < c
(при том же числе степеней свободы n), тем легче выполняется условие c2 < c 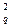 и принимается проверяемая гипотеза. Но при этом увеличивается вероятность ошибки второго рода. В связи с этим нецелесообразно принимать 0,02<q<0,01.
и принимается проверяемая гипотеза. Но при этом увеличивается вероятность ошибки второго рода. В связи с этим нецелесообразно принимать 0,02<q<0,01.
Дата: 2019-02-02, просмотров: 379.