Косвенные измерения — это измерения, при которых искомое значение Y находят на основании известной зависимости:
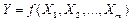 ,
,
где X 1 , X 2 ,..., Xm - значения, полученные при прямых измерениях. По виду функциональной зависимости они делятся на две основные группы — линейные и нелинейные. Для линейных косвенных измерений математический аппарат статистической обработки полученных результатов разработан детально. Обработка результатов косвенных измерений производится, как правило, методами, основанными на раздельной обработке аргументов и их погрешностей, линеаризации, приведения, перебора.
Методика обработки результатов косвенных измерений приведена в документе МИ 2083-90 "ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей".
Косвенные измерения при линейной зависимости между аргументами. Линейная функциональная зависимость является простейшей формой связи между измеряемой величиной и находимыми посредством прямых измерений аргументами. Она может быть выражена формулой:
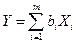 ,
,
где bi - постоянный коэффициент i-го аргумента Xi; m - число аргументов.
Погрешности линейных косвенных измерений оцениваются методом, основанным на раздельной обработке аргументов и их погрешностей.
Если коэффициенты bi определяют экспериментально, то нахождение результата измерения величины Y производится поэтапно. Сначала оценивают каждое слагаемое 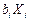 как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины Y. Результат косвенного измерения определяют по формуле:
как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины Y. Результат косвенного измерения определяют по формуле:

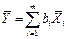 ,
,
где 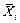 - оценка результата измерений аргумента
- оценка результата измерений аргумента 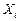 , получаемая, как правило, посредством обработки результатов многократных прямых измерений каждого из аргументов. При несмещенности и состоятельности результатов полученная оценка результата измерения
, получаемая, как правило, посредством обработки результатов многократных прямых измерений каждого из аргументов. При несмещенности и состоятельности результатов полученная оценка результата измерения 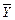 будет также несмещенной и состоятельной. Поскольку дисперсия результата измерения:
будет также несмещенной и состоятельной. Поскольку дисперсия результата измерения:
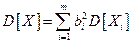 ,
, 
то, если результаты 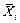 обладают минимальной дисперсией, т.е. являются эффективными, то и оценка результата измерения
обладают минимальной дисперсией, т.е. являются эффективными, то и оценка результата измерения 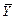 также будет эффективной.
также будет эффективной.
При отсутствии корреляционной связи между аргументами, СКО результата косвенного измерения S 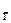 , обусловленное случайными погрешностями, вычисляется по формуле:
, обусловленное случайными погрешностями, вычисляется по формуле:
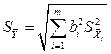 ,
,
где S 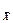 - среднее квадратическое отклонение (СКО) результата измерения аргумента
- среднее квадратическое отклонение (СКО) результата измерения аргумента 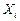 .
.
При наличии корреляционной связи между аргументами СКО результата косвенного измерения:
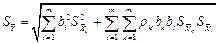 .
.
Здесь 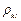 - несмещенная оценка коэффициента корреляции между погрешностями аргументов
- несмещенная оценка коэффициента корреляции между погрешностями аргументов 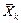 и
и 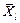 .
.
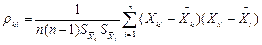 ,
,
где 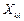 ,
, 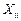 - i-e результаты прямых измерений k-ro и l-го аргументов; n - число прямых измерений аргументов. Коэффициент корреляции может быть рассчитан и по другим формулам, равнозначным приведенной.
- i-e результаты прямых измерений k-ro и l-го аргументов; n - число прямых измерений аргументов. Коэффициент корреляции может быть рассчитан и по другим формулам, равнозначным приведенной.
Корреляция между аргументами чаще всего возникает в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий (температуры, влажности, напряжения питающей сети, помех и т.п.). Критерием отсутствия связи между двумя аргументами является выполнение неравенства
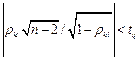 ,
,
где tq - коэффициент Стьюдента, соответствующий уровню значимости q и числу степеней свободы f = n-2 (Приложение 1). Необходимо проверить отсутствие корреляционных связей между всеми парными сочетаниями аргументов.
Моделью для распределения результатов измерений отдельных аргументов обычно можно считать случайную величину с нормальным распределением. Для распределений, отличных от нормального, распределение среднего арифметического при этом все же можно считать нормальным. Случайную погрешность результата косвенного измерения, образующуюся путем сложения случайных погрешностей результатов определения многих аргументов, еще с большим основанием можно считать нормально распределенной случайной величиной. Это дает возможность найти доверительный интервал для значения измеряемой величины.
При большом числе измерений (более 25-30), выполненных при нахождении каждого из аргументов, доверительную границу случайной погрешности результата косвенного измерения можно определить по формуле:
δ 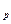 = zp S
= zp S  ,
,
где zp - квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р (см. Приложение 1).
При меньшем числе измерений для определения доверительного интервала используется распределение Стьюдента, число степеней свободы которого рассчитывается по приближенной формуле:

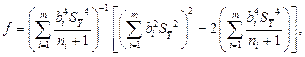
где n i - число измерений при определении аргумента 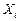 . В этом случае при условии, что распределение погрешностей результатов измерения аргументов не противоречит нормальному распределению, доверительная граница случайной погрешности результата косвенного измерения
. В этом случае при условии, что распределение погрешностей результатов измерения аргументов не противоречит нормальному распределению, доверительная граница случайной погрешности результата косвенного измерения
δ 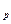 = tp S
= tp S  ,
,
где tp – коэффициент Стьюдента, соответствующий доверительной вероятности P и числу степеней свободы f (Приложение 1).
Систематическая погрешность результата косвенного измерения определяется систематическими погрешностями результатов измерений аргументов. При измерениях последние стремятся исключить. Однако полностью это сделать не удается, всегда остаются неисключенные систематические погрешности, которые рассматриваются как реализации случайной величины, имеющей равномерное распределение. Такое предположение приводит обычно к достаточно осторожным заключениям о погрешности результатов косвенных измерений.
Доверительные границы неисключенной систематической погрешности результата линейного косвенного измерения q (Р) в случае, если неисключенные систематические погрешности аргументов заданы границами q i, вычисляют по формуле:
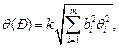
где k - поправочный коэффициент, определяемый принятой доверительной вероятностью Р и числом m составляющих q i. Его значения приведены в табл. 3.1. Погрешность от применения этих усредненных коэффициентов не превышает 10% .
Таблица 3.1 Значения вероятности P и коэффициента k при m>4
| Р | 0,90 | 0,95 | 0,98 | 0,99 |
| k | 0,95 | 1,1 | 1,3 | 1,4 |
Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы их доверительными границами q i ( Pi ), соответствующие вероятностям Pi, то границу q (Р) определяют по формуле:
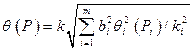 .
.
Коэффициенты k i определяются так же, как поправочный коэффициент k .
Суммарная погрешность результата косвенного измерения оценивается на основе композиции распределений случайных и неисключенных систематических погрешностей. Формулы для ее расчета в зависимости от соотношения границ неисключенной систематической составляющей и СКО случайной составляющей погрешности приведены в табл. 3.2.Коэффициент k р определяется по табл. 3.3.
Результат косвенных измерений должен записываться в виде:
х ± D Р ; Р=….
Таблица 3.2 Погрешность результата косвенного измерения
| Значение отношения | Погрешность результата измерения |
1) 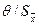 < 0,8 < 0,8
| ∆ = 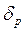
|
2) 0,8 ≤ 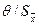 ≤ 8 ≤ 8
| ∆ = k 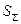 = 2( = 2( 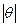 + + 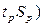
|
3) 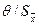 > 8 > 8
| ∆ = 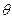
|
Таблица 3.3 Зависимость kp от отношения q (Р)/ S 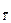 при различной доверительной вероятности
при различной доверительной вероятности
q (Р)/ S 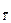
| 0,5 | 0,75 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| k 0,95 | 0,81 | 0,77 | 0,74 | 0,71 | 0,73 | 0,76 | 0,78 | 0,79 | 0,80 | 0,81 |
| k 0,99 | 0,87 | 0,85 | 0,82 | 0,80 | 0,81 | 0,82 | 0,83 | 0,83 | 0,84 | 0,85 |
Косвенные измерения при нелинейной зависимости между аргументами. Для обработки результатов измерений при нелинейных зависимостях между аргументами и некоррелированных погрешностях используется метод линеаризации. Он состоит в том, что нелинейная функция, связывающая измеряемую величину с аргументами, разлагается в ряд Тейлора:
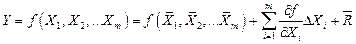 .
.
Здесь 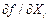 - первая частная производная от функции
- первая частная производная от функции 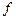 по аргументу
по аргументу 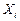 , вычисленная в точке
, вычисленная в точке 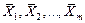 ;
; 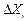 - отклонение результата измерения аргумента
- отклонение результата измерения аргумента 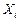 от его среднего арифметического;
от его среднего арифметического; 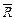 - остаточный член:
- остаточный член:

Метод линеаризации применим, если остаточным членом можно пренебречь. Это возможно в том случае, если:
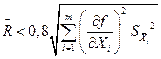 ,
,
где S 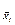 - СКО случайной погрешности результата измерений аргумента
- СКО случайной погрешности результата измерений аргумента 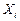 . При необходимости результаты косвенных измерений можно уточнить, используя члены ряда Тейлора более высокого порядка. Оценка результата определяется по формуле:
. При необходимости результаты косвенных измерений можно уточнить, используя члены ряда Тейлора более высокого порядка. Оценка результата определяется по формуле:
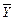 =
= 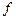 (
( 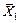 ,
,  ,…,
,…, 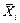 ).
).
Абсолютная погрешность косвенного измерения 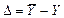 :
: 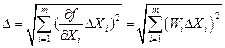 ,
,
где 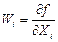 - коэффициенты влияния i-го аргумента;
- коэффициенты влияния i-го аргумента; 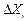 - абсолютная погрешность измерения i-го аргумента;
- абсолютная погрешность измерения i-го аргумента; 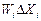 - частная i-ая погрешность определения результата косвенного измерения.
- частная i-ая погрешность определения результата косвенного измерения.
Оценка СКО случайной погрешности результата косвенного измерения:
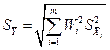 .
.
Доверительные границы случайной погрешности результата при нормально распределенных погрешностях измерений аргументов вычисляются так же, как и для линейных косвенных измерений, при условии, что вместо коэффициентов bi в формулах подставляются коэффициенты влияния Wi. Аналогичным образом поступают при определении границ неисключенной систематической погрешности. Погрешность результата нелинейных косвенных измерений оценивается так же, как и при линейных измерениях.
Задача 3.1
Расход отходящих газов, приведенный к нормальным условиям, определяется через расход газа в рабочих условиях (QРУ), давление в рабочих условиях (PРУ) и температуру в рабочих условиях (TРУ) по формуле:
QНУ = (QРУ . PРУ . TНУ) / (TРУ . PНУ) = (QРУ . PРУ . 293) / (TРУ . 1013) = =(0,289 . QРУ . PРУ) / TРУ,
Выполнены прямые измерения в рабочих условиях расхода газа, давления, температуры и получены следующие результаты (таблица 3.4). Определить значение расхода газа QНУ и границы доверительного интервала при Р=0,95. 
Для вариантов 26 и больше данные выбираются следующим образом: из варианта вычитается число 20, н-р 26-20 = 6, берутся результаты этого варианта и все значения увеличиваются на 26 (на номер варианта).
Таблица 3.4 – Исходные данные
| № варианта | Измеряемые величины | Результаты измерений |
| 1. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4500 4490 4510 4500 1025 1027 1026 1026 1025 1027 1650 1400 1645 1655 1645 |
| 2. | QРУ, м 3/мин PРУ, гПа TРУ, К | 9000 8990 9010 9000 1030 1028 1032 1030 1080 1600 1595 1605 1600 |
| 3. | QРУ, м 3/мин PРУ, гПа TРУ, К | 2100 2095 2100 2100 2105 1035 1033 1035 1037 1705 1710 1715 1710 |
| 4. | QРУ, м 3/мин PРУ, гПа TРУ, К | 3050 3045 3055 3050 1037 1037 1035 1035 1670 1670 1675 1605 1665 |
| 5. | QРУ, м 3/мин PРУ, гПа TРУ, К | 6540 6535 6545 6540 1050 1048 1050 1000 1052 1660 1670 1665 1670 1660 |
| 6. | QРУ, м 3/мин PРУ, гПа TРУ, К | 5010 5005 5010 5015 5010 1042 1044 1043 1043 1630 1625 1635 1630 1690 1630 |
| 7. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4000 4010 4005 3990 3995 925 927 926 927 928 924 1630 1620 1400 1635 1625 |
| 8. | QРУ, м 3/мин PРУ, гПа TРУ, К | 8000 7990 8000 8010 1130 1128 1128 1005 1120 1125 1500 1510 1490 1510 1505 |
| 9. | QРУ, м 3/мин PРУ, гПа TРУ, К | 2200 2195 2200 2400 2200 2190 935 933 934 936 1605 1610 1615 1610 1610 |
| 10. | QРУ, м 3/мин PРУ, гПа TРУ, К | 3150 3145 3155 3050 3140 1135 1130 1130 1130 1570 1570 1575 1565 1575 |
| 11. | QРУ, м 3/мин PРУ, гПа TРУ, К | 5540 5545 5535 5545 5545 1050 1040 1280 1045 1045 1670 1660 1670 1665 |
| 12. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4990 4980 4985 4980 4980 1040 1035 1040 1280 1040 1650 1645 1655 1650 1710 1650 |
| 13. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4470 4460 4480 4470 4800 1022 1024 1023 1023 1022 1550 1300 1545 1555 1550 1545 |
| 14. | QРУ, м 3/мин PРУ, гПа TРУ, К | 8900 8890 8010 8895 8890 1020 1018 1022 1020 1630 1625 1635 1630 1625 |
| 15. | QРУ, м 3/мин PРУ, гПа TРУ, К | 2150 2000 2145 2150 2150 2155 1050 1048 1050 1052 1050 1690 1695 1700 1695 1700 |
| 16. | QРУ, м 3/мин PРУ, гПа TРУ, К | 3075 3070 3080 3075 3075 1030 1030 1028 1028 1025 1620 1620 1625 1550 1615 |
| 17. | QРУ, м 3/мин PРУ, гПа TРУ, К | 6500 6495 6505 6500 1020 1018 1020 1022 1020 1660 1650 1655 1650 |
| 18. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4010 4005 4010 4015 4010 4005 1047 1049 1048 1048 1047 1600 1595 1605 1605 1600 |
| 19. | QРУ, м 3/мин PРУ, гПа TРУ, К | 3970 3980 3075 3960 915 917 926 921 920 1620 1610 1625 1615 1615 1615 |
| 20. | QРУ, м 3/мин PРУ, гПа TРУ, К | 7000 6990 7000 7000 7010 7005 1150 1148 1148 1145 1140 1525 1535 1515 1535 1530 1525 |
| 21. | QРУ, м 3/мин PРУ, гПа TРУ, К | 2700 2695 2700 2900 2700 2690 945 943 944 946 945 1620 1625 1630 1625 |
| 22. | QРУ, м 3/мин PРУ, гПа TРУ, К | 3450 3445 3455 3350 3440 3450 1130 1125 1125 1120 1120 1580 1580 1585 1575 1585 |
| 23. | QРУ, м 3/мин PРУ, гПа TРУ, К | 5470 5475 5465 5475 5470 1080 1070 1075 1075 1075 1070 1570 1560 1570 1565 1560 |
| 24. | QРУ, м 3/мин PРУ, гПа TРУ, К | 4960 4950 4955 4950 4950 4955 940 935 940 935 930 1550 1545 1745 1540 1545 1550 |
| 25. | QРУ, м 3/мин PРУ, гПа TРУ, К | 2210 2195 2200 2200 2195 2200 1040 1038 1035 1040 1710 1715 1715 1710 1710 |
Дата: 2019-02-02, просмотров: 359.