Совместные измерения выполняются с целью определения функциональной зависимость между физическими величинами:
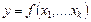

При этом совместно измеряют значения аргументов 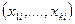 и соответствующие значения величины
и соответствующие значения величины 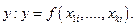 По полученным экспериментальным данным
По полученным экспериментальным данным 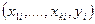 строят функциональную зависимость.
строят функциональную зависимость.
Уравнения измерения имеют вид:
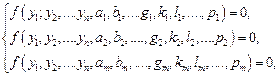
где 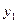 …
… 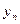 - искомые величины;
- искомые величины; 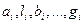 - величины измеряемые прямым или косвенным методом;
- величины измеряемые прямым или косвенным методом; 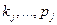 - постоянные величины.
- постоянные величины.
Характерной особенностью является то, что число уравнений больше числа измеряемых величин.
Вид линейной зависимости непосредственно измеряемых величин с искомыми уравнениями имеют вид:
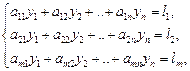
где 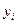 - величины, подлежащие измерению при совместных измерениях;
- величины, подлежащие измерению при совместных измерениях;
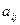 - известные коэффициенты;
- известные коэффициенты;
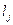 - непосредственно измеряемые величины;
- непосредственно измеряемые величины;
n - число искомых величин;
m- число уравнений.
Т.к. m>n из-за номинальных погрешностей, нет возможности найти такие значения величин, которые одновременно удовлетворяли всем уравнениям системы. Эти уравнения называются условными.
При подстановке в систему условных уравнений результатов прямых измерений возникают погрешности 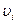 , называемые невязками. Поэтому уравнения системы необходимо скорректировать:
, называемые невязками. Поэтому уравнения системы необходимо скорректировать:
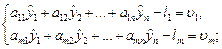
где 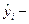 оценки величин
оценки величин 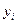 максимально приближенные к ним по свойствам.
максимально приближенные к ним по свойствам.
Для нахождения этих оценок используется метод наименьших квадратов (МНК). В этом методе оценки параметров зависимости определяются из условия, что сумма квадратов отклонения расчётных значений от экспериментальных минимальна.
Таким образом, оценки 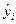 находят из условия:
находят из условия:
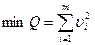 .
.
Рассмотрим случай зависимости для двух искомых величин 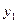 и
и 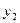 :
:
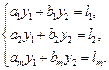
Заменяя 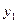 и
и 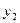 их оценками
их оценками 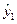 и
и 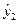 :
:
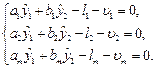
Для нахождения оценок и реализации МНК необходимо найти частные производные и приравнять их к нулю:
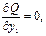
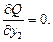
Уравнения системы называются нормальными. Систему уравнений можно записать в виде:
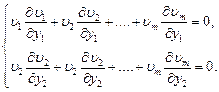
Значение производных будут равны: 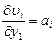 ;
; 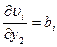 .
.
После преобразований уравнения выглядят следующим образом:
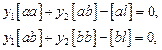
где 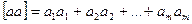 ;
;
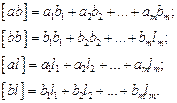
Для n измеряемых величин системы условных и нормальных уравнений имеют вид:
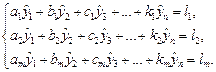
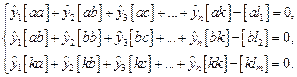
Т.к. число нормальных уравнений равно числу неизвестных, то эти уравнения записываются через определители:
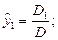
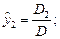 ….
…. 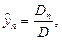
где 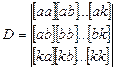 - главный определитель.
- главный определитель.
Частные определители получают путём замены соответствующего столбца с коэффициентами при неизвестных 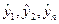 на столбец со свободными членами. Например:
на столбец со свободными членами. Например:
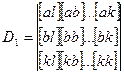 .
.
Оценки СКО величин, найденных при совместных измерениях определяются по следующим формулам:
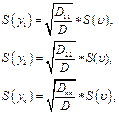
где 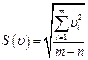 - оценка СКО условных уравнений;
- оценка СКО условных уравнений;
невязки 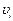 рассчитываются при подстановке в каждое условное уравнение найденных оценок искомых величин
рассчитываются при подстановке в каждое условное уравнение найденных оценок искомых величин 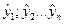
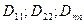 - алгебраические дополнения главного определителя
- алгебраические дополнения главного определителя 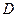 , получаемые путём удаления из матрицы определителя
, получаемые путём удаления из матрицы определителя 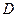 столбца и строки, на пересечении которых находится соответствующий элемент, например:
столбца и строки, на пересечении которых находится соответствующий элемент, например:
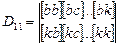
Доверительный интервал определяют по формуле:
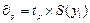 ,
,
где 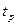 - коэффициент Стьюдента (Приложение 1) при заданной доверительной вероятности р и числе степеней свободы
- коэффициент Стьюдента (Приложение 1) при заданной доверительной вероятности р и числе степеней свободы 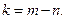
Задача 2.1
По содержанию фосфора в хромовой руде спектрографическим методом [P]С получены результаты, приведенные в таблице 2.4. В качестве арбитражного метода применялось определение фосфора фотометрическим методом [P]Ф.
Таблица 2.4
| Вариант | 1 | 2 | 3 | Номер 4 | пробы 5 | 6 | 7 | 8 |
| 1. [P]С [P]ф | 0,020 0,024 | 0,024 0,029 | 0,036 0,042 | 0,044 0,049 | 0,030 0,034 | 0,041 0,045 | 0,035 0,040 | 0,021 0,024 |
| 2. [P]С [P]ф | 0,020 0,024 | 0,035 0,039 | 0,045 0,050 | 0,023 0,026 | 0,040 0,044 | 0,027 0,030 | 0,037 0,041 | 0,042 0,047 |
| 3. [P]С [P]ф | 0,047 0,052 | 0,039 0,043 | 0,036 0,029 | 0,031 0,034 | 0,042 0,046 | 0,021 0,024 | 0,022 0,024 | 0,036 0,040 |
| 4. [P]С [P]ф | 0,031 0,035 | 0,038 0,042 | 0,045 0,050 | 0,024 0,027 | 0,049 0,054 | 0,029 0,033 | 0,020 0,022 | 0,033 0,036 |
| 5. [P]С [P]ф | 0,040 0,045 | 0,045 0,050 | 0,030 0,033 | 0,025 0,028 | 0,037 0,041 | 0,042 0,046 | 0,033 0,037 | 0,022 0,025 |
| 6. [P]С [P]ф | 0,018 0,022 | 0,035 0,040 | 0,044 0,049 | 0,025 0,028 | 0,039 0,043 | 0,028 0,031 | 0,036 0,040 | 0,040 0,045 |
| 7. [P]С [P]ф | 0,030 0,034 | 0,039 0,043 | 0,045 0,049 | 0,026 0,029 | 0,047 0,052 | 0,031 0,035 | 0,021 0,023 | 0,034 0,037 |
| 8. [P]С [P]ф | 0,049 0,055 | 0,041 0,045 | 0,039 0,031 | 0,033 0,037 | 0,044 0,049 | 0,024 0,028 | 0,024 0,029 | 0,039 0,045 |
| 9. [P]С [P]ф | 0,036 0,039 | 0,043 0,047 | 0,051 0,055 | 0,029 0,032 | 0,054 0,060 | 0,033 0,038 | 0,025 0,029 | 0,037 0,042 |
| 10. [P]С [P]ф | 0,035 0,040 | 0,040 0,046 | 0,025 0,030 | 0,019 0,023 | 0,032 0,037 | 0,037 0,042 | 0,028 0,033 | 0,018 0,022 |
| 11. [P]С [P]ф | 0,032 0,035 | 0,038 0,041 | 0,045 0,051 | 0,023 0,027 | 0,049 0,053 | 0,028 0,033 | 0,020 0,023 | 0,033 0,037 |
| 12. [P]С [P]ф | 0,040 0,044 | 0,045 0,049 | 0,030 0,032 | 0,025 0,029 | 0,037 0,040 | 0,042 0,045 | 0,034 0,037 | 0,022 0,026 |
| 13. [P]С [P]ф | 0,018 0,021 | 0,035 0,041 | 0,044 0,048 | 0,025 0,029 | 0,038 0,043 | 0,029 0,031 | 0,036 0,041 | 0,042 0,045 |
| 14. [P]С [P]ф | 0,049 0,054 | 0,042 0,045 | 0,039 0,033 | 0,033 0,036 | 0,044 0,048 | 0,025 0,028 | 0,023 0,029 | 0,039 0,041 |
| 15. [P]С [P]ф | 0,036 0,038 | 0,043 0,048 | 0,052 0,055 | 0,029 0,033 | 0,054 0,061 | 0,033 0,039 | 0,026 0,029 | 0,037 0,045 |
| 16. [P]С [P]ф | 0,036 0,040 | 0,040 0,048 | 0,024 0,030 | 0,019 0,024 | 0,032 0,035 | 0,037 0,041 | 0,026 0,033 | 0,019 0,022 |
| 17. [P]С [P]ф | 0,021 0,024 | 0,024 0,027 | 0,036 0,040 | 0,044 0,046 | 0,030 0,035 | 0,040 0,045 | 0,035 0,042 | 0,021 0,025 |
| 18. [P]С [P]ф | 0,022 0,024 | 0,035 0,041 | 0,045 0,051 | 0,023 0,028 | 0,041 0,044 | 0,027 0,032 | 0,038 0,041 | 0,042 0,046 |
| 19. [P]С [P]ф | 0,040 0,044 | 0,045 0,052 | 0,030 0,033 | 0,025 0,029 | 0,037 0,042 | 0,042 0,044 | 0,031 0,037 | 0,021 0,025 |
| 20. [P]С [P]ф | 0,049 0,056 | 0,041 0,044 | 0,031 0,035 | 0,032 0,037 | 0,046 0,049 | 0,024 0,027 | 0,024 0,029 | 0,039 0,043 |
[P]ф, [P]С - концентрация фосфора в руде, определенная фотометрическим методом и спектрографическим соответственно, %.
Доверительная погрешность анализа на содержание фосфора dР = ±0,002 %. Определить наличие и характер методической систематической погрешности в анализе руды, спектрографическим методом, поправку и представить исправленные результаты.
Задача 2.2
Температура измерялась одновременно комплектом вольфрамрений-вольфрамрениевой (ТВР) термопарой с показывающим измерительным прибором и комплектом платинородий-платиновой (ТПП) термопарой с показывающим измерительным прибором. Вторая термопара является образцовой и имеет доверительную погрешность dР = ±5 °С. В результате экспериментов получены следующие данные:
Таблица 2.5
| № | Температура | |||||||||
| 21. tВ tП | 1600 1585 | 1605 1595 | 1635 1615 | 1635 1620 | 1620 1610 | 1615 1600 | 1610 1595 | 1625 1610 | 1605 1590 | |
| 22. tВ tП | 1600 1595 | 1605 1600 | 1635 1615 | 1610 1600 | 1620 1600 | 1625 1615 | 1610 1595 | 1615 1605 | ||
| 23. tВ tП | 1635 1615 | 1605 1600 | 1620 1605 | 1600 1595 | 1615 1605 | 1610 1600 | 1625 1605 | 1630 1615 | ||
| 24. tВ tП | 1640 1620 | 1600 1590 | 1615 1600 | 1610 1600 | 1625 1610 | 1635 1625 | 1595 1585 | 1620 1605 | 1615 1625 | |
| 25. tВ tП | 1595 1585 | 1635 1620 | 1620 1600 | 1625 1615 | 1610 1600 | 1640 1620 | 1615 1605 | 1600 1590 | 1595 1612 | |
| 26. tВ tП | 1650 1630 | 1625 1610 | 1635 1620 | 1605 1595 | 1630 1615 | 1645 1635 | 1620 1610 | 1610 1600 | ||
| 27. tВ tП | 1620 1605 | 1605 1590 | 1610 1595 | 1615 1605 | 1595 1580 | 1600 1590 | 1630 1610 | 1630 1615 | ||
| 28. tВ tП | 1605 1600 | 1640 1620 | 1625 1605 | 1615 1600 | 1620 1610 | 1630 1620 | 1615 1605 | 1610 1605 | 1615 1625 | |
| 29. tВ tП | 1610 1600 | 1620 1610 | 1605 1595 | 1600 1595 | 1595 1590 | 1630 1610 | 1615 1595 | 1605 1590 | ||
| 30. tВ tП | 1635 1620 | 1620 1610 | 1635 1610 | 1615 1605 | 1605 1600 | 1640 1620 | 1610 1605 | 1625 1610 | ||
| 31. tВ tП | 1600 1595 | 1630 1610 | 1595 1590 | 1615 1600 | 1605 1595 | 1610 1600 | 1625 1610 | 1620 1600 | ||
| 32. tВ tП | 1645 1625 | 1615 1605 | 1605 1595 | 1630 1615 | 1620 1605 | 1640 1630 | 1600 1590 | 1625 1615 | ||
| 33. tВ tП | 1590 1580 | 1615 1600 | 1620 1605 | 1630 1620 | 1605 1595 | 1595 1585 | 1610 1595 | 1635 1615 | 1600 1590 | |
| 34. tВ tП | 1615 1605 | 1620 1610 | 1645 1625 | 1605 1595 | 1600 1590 | 1625 1605 | 1640 1625 | 1630 1620 | ||
| 35. tВ tП | 1615 1595 | 1590 1580 | 1620 1610 | 1630 1615 | 1610 1600 | 1605 1595 | 1595 1585 | 1635 1615 | 1640 1625 | |
| 36. tВ tП | 1615 1605 | 1625 1615 | 1605 1600 | 1605 1595 | 1580 1575 | 1635 1625 | 1620 1600 | 1610 1595 | ||
| 37. tВ tП | 1645 1625 | 1630 1615 | 1620 1605 | 1600 1590 | 1640 1630 | 1615 1605 | 1605 1595 | 1600 1595 | ||
| 38. tВ tП | 1625 1610 | 1610 1595 | 1615 1600 | 1620 1610 | 1600 1585 | 1605 1595 | 1635 1615 | 1630 1615 | 1615 1605 | |
| 39. tВ tП | 1600 1595 | 1635 1615 | 1620 1600 | 1610 1595 | 1615 1605 | 1625 1615 | 1615 1600 | 1610 1595 | 1605 1600 | |
| 40. tВ tП | 1615 1605 | 1625 1615 | 1610 1600 | 1605 1600 | 1595 1500 | 1630 1610 | 1620 1600 | 1610 1595 | 1605 1590 | |
| 41. tВ tП | 1635 1620 | 1620 1610 | 1625 1605 | 1615 1605 | 1600 1595 | 1640 1620 | 1630 1615 | 1605 1600 | 1625 1610 | |
| 42. tВ tП | 1600 1595 | 1625 1605 | 1590 1585 | 1620 1605 | 1605 1595 | 1615 1605 | 1620 1605 | 1620 1600 | 1615 1595 | |
| 43. tВ tП | 1650 1630 | 1615 1605 | 1605 1595 | 1625 1610 | 1620 1605 | 1635 1625 | 1610 1600 | 1600 1590 | 1625 1610 | |
| 44. tВ tП | 1605 1600 | 1635 1615 | 1625 1605 | 1615 1600 | 1650 1635 | 1630 1620 | 1615 1605 | 1610 1605 | 1630 1615 | |
| 45. tВ tП | 1620 1610 | 1630 1620 | 1615 1605 | 1610 1605 | 1600 1590 | 1635 1610 | 1620 1605 | 1615 1595 | 1605 1595 | |
tВ, tП - температура, измеренная термопарами ТВР и ТПП, соответственно, °С.
Определить наличие и характер поведения инструментальной систематической погрешности в измерении температуры вольфрамрениевой термопарой, поправку и представить исправленные результаты измерения температуры вольфрамрениевой термопарой.
Дата: 2019-02-02, просмотров: 383.