Система предпочтительных чисел
Предпочтительным числам свойственны определенные математические закономерности. Наипростейшие ряды предпочтительных чисел строятся на основе арифметической прогрессии. Ряды предпочтительных чисел, основанные на арифметической прогрессии, используются в параметрической стандартизации редко (ГОСТ на размер обуви). Достоинства таких рядов - простота, недостаток- относительная неравномерность.
С древнейших времен для построения рядов предпочтительных чисел использовалась геометрическая прогрессия. Геометрическая прогрессия имеет ряд полезных свойств, используемых в стандартизации и являющихся ее достоинствами.
Ряды предпочтительных чисел строятся на основе геометрической прогрессии со знаменателем вида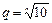 
, где n = 5,10,20,40, 80,160.
Соответствующие им ряды обозначаются: R5, R10, R20, R40 - основные ряды; R80, R160 - дополнительные ряды (см. Приложение 1)
Для использования на практике рекомендуют пользоваться основными рядами (желательно R5).
Свойства рядов предпочтительных чисел
1.ГОСТ устанавливает стандартные значения предпочтительных чисел в диапазоне от нуля до плюс бесконечности, на основе фиксированных значений предпочтительных чисел, включенных в десятичный интервал от 1 до 10. Для перехода из интервала от 1 до 10 в любой другой десятичный интервал нужно умножить числа на величину 10к, где к - целое положительное или отрицательное число. Практически умножение предпочтительных чисел на 10к сводится к переносу запятой, входящей в каждое число, на к знаков вправо (при положительном к) и на к знаков влево (при отрицательном к);
2.Номер ряда предпочтительных чисел указывает на количество чисел в десятичном интервале. Исключение: число 1 не входит в десятичный интервал от 1 до 10. Его следует рассматривать как завершающее число предыдущего десятичного интервала;
3.Ряд R40 включает все основные ряды предпочтительных чисел (R5, R10, R20). Ряд R5: 1,0 - 1,6 - 2,5 - 4,0 - 6,3 - 10,0. (все остальные числа ряда R40 округляются до «сотых») Номера чисел ряда R5 в ряду R40 кратны 8;
4.Число 3,15 (двадцатый член ряда R40) стандартизаторы используют в своей практике в качестве числа «ПИ». Неточность, вносимая при этом, не превышает 0,03%. Использование в расчетах этого числа позволяет выражать предпочтительными числами длины окружности, площади кругов, угловые скорости, цилиндрические и сферические поверхности и объемы;
5.По номеру предпочтительного числа можно рассчитать значение этого числа по следующей формуле: а = qn .
Обозначения рядов предпочтительных чисел
R5, R10, R20, R40 являются рядами неограниченными никакими пределами.
Ряды с ограниченными пределами обозначаются:
R40(75 ... 300) - это основной ряд R40, ограниченный сверху и снизу членами 75 и 300 и включающий оба эти члена.
R40(75 ... ) - это основной ряд R40, ограниченный снизу членом 75 включительно.
R40( ... 300) - это основной ряд R40, ограниченный сверху членом 300 включительно.
В стандартизации используются выборочные ряды. Они применяются в тех случаях, когда ни одна из градаций основных рядов не удовлетворяет поставленным требованиям. Обычно по выборочным рядам строят ряды параметров и размеров, являющихся функциями других параметров и размеров, для которых градации приняты по основным рядам. Выборочные ряды предпочтительных чисел получают отбором каждого 2, 3, 4 ... n члена ряда, начиная с любого члена ряда
R20/3 (14 ... 40) - это выборочный ряд, составленный из каждого третьего члена основного ряда R20, ограниченного сверху и снизу членами 14 и 40 включительно.
В радиоэлектронике параметрические стандарты приведены в соответствие с рекомендациями международной электротехнической комиссии. Этими рекомендациями установлены предпочтительные числа рядов: Е3, Е6, Е12, Е24, Е48, Е96, Е192. эти ряды применяются при установлении номинальной емкости конденсаторов, номинального сопротивления резистора.
Методы стандартизации
Стандартизация базируется на нескольких основных методах, обеспечивающих достижение взаимозаменяемости и специализации на разных уровнях. Основные методы стандартизации: унификация, симплификация, агрегатирование и типизация.
Унификация – это метод стандартизации, заключающийся в рациональном сокращении количества, размеров, типов, видов, деталей, узлов и других объектов одинакового функционального назначения до количества технически и экономически целесообразного.
Первый этап работ при осуществлении унификации – определение уровня унификации, под которым понимается насыщенность изделий унифицированными составными элементами.
Уровень унификации определяется следующими показателями:
Показатель уровня унификации по количеству унифицированных деталей:
УД=(КУ/КД) × 100%,
где КУ – количество унифицированных деталей; КД – общее количество деталей.
Показатель уровня унификации по весу унифицированных деталей:
УВ=(ВУ/ВО) × 100%,
где ВУ – вес всех унифицированных деталей в партии; ВО – общий вес изделия.
Показатель уровня унификации по трудоемкости изготовления унифицированных деталей:
УТ=(ТС/ТП) × 100%,
где ТС - суммарная трудоемкость изготовления унифицированных деталей; ТП – полная трудоемкость изготовления изделия.
Под унифицированными необходимо понимать стандартные, покупные и заимствованные детали:
ДУ=НС+НЗ+НП,
где ДУ – количество унифицированных деталей; НС – количество стандартных деталей; НЗ – количество заимствованных деталей; НП – количество покупных деталей.
Подставляя ДУ в выражения для УТ, УВ, УД, можно получить для них окончательные выражения.
Каждый из приведенных показателей характеризует уровень унификации только с одной какой-либо стороны.
Более полную характеристику уровня унификации изделия дает комплексный показатель уровня унификации.
Этот показатель определяется как отношение части производственных затрат на изготовление унифицированных деталей к производственным затратам на изготовление всего изделия:
У=((ВУ × СУ+ТС × Р)/(ВО × СД+ТП × Р)),
где СУ - средняя стоимость единицы веса материала унифицированных деталей; СД – средняя стоимость единицы веса материала изделия в целом; Р – средняя стоимость нормо-часа.
Симплификация – это разновидность или метод стандартизации, заключающийся в простом сокращении количества размеров, деталей, узлов, типов, видов и объектов до количества экономически и технически целесообразного.
Агрегатирование – это метод стандартизации, заключающийся в создании изделий из ограниченного количества стандартных деталей или узлов, обладающих геометрической и функциональной взаимозаменяемостью.
Под взаимозаменяемостью следует понимать такое состояние деталей, узлов, блоков, входящих в изделие, при котором изделие сохраняет свои функциональные свойства.
Различают геометрическую и функциональную взаимозаменяемость.
Геометрическая взаимозаменяемость – обеспечивает сборку или замену деталей, узлов, блоков по геометрическим параметрам, включающим форму и размеры деталей, взаимное расположение, шероховатость и волнистость их поверхностей.
Функциональная взаимозаменяемость – предусматривает обеспечение помимо взаимозаменяемости по геометрическим параметрам также взаимозаменяемость по электрическим, магнитным, механическим, физико-химическим и другим эксплуатационным показателям.
Типизация – это разновидность или метод стандартизации, заключающийся в рациональной разработке и установлении типовых конструктивных, технологических и других решений. Типизация может решать задачи развития целой отрасли промышленности. В основе проведения типизации лежит система предпочтительных чисел.
Примеры решения задач
Пример 1. Рассчитайте 7 значений линейного параметра в области от 3,15 до 50 мм по геометрической прогрессии используя ГОСТ 6636-69, проведите нормализацию этого параметра.
Решение:
Искомый ряд будет иметь следующий вид:
А; Ах; Ах2; Ах3; Ах4; Ах5; Ах6; где А=3,15; Ах6=50
Отсюда х = (50/3,15)1/6 = 1,586 – знаменатель ряда.
Вычислим значения ряда:
3,15; 4,98; 7,89; 12,53; 19,87; 31,51; 49,97.
Знаменатель полученного ряда близок к знаменателю ряда R 5=1,585, а вычисленным членам ряда соответствуют следующие члены ряда R 10 (Приложение 1):
3,15; 5; 8; 12,5; 20; 31,5; 50.
Эти числа являются каждым вторым членом ряда R 10 в указанном диапазоне, т.е. рассчитанные нами значения линейного параметра соответствуют выборочному ряду R 10/2.
Пример 2. Определите ряды параметра V (объем резервуара), если известно, что связь между объемом V и диаметром D резервуара имеет следующий вид: V = p D 2 H /4.
Параметр D задан рядом R 5/2 (1,0м …16,0м), p =3,14, а высота резервуара H =5,0 м.
Решение:
На основе системы предпочтительных чисел (ГОСТ 8032 – 84) находим ряд параметра D и определяем его знаменатель:
R 5/4 (1,0 … 16,0)=1,0; 2,5; 6,3; 16,0 м. Знаменатель этого ряда х=2,5/1,0=2,5.
Найденным членам ряда соответствуют номера 0; 16; 32; 48; числу p - номер 20, числу 4 – номер 24 и числу 5 – номер 28.
Определим номера членов ряда объема резервуара, воспользовавшись свойствами геометрической прогрессии:
NV1=20+2 ×0-24+28=24
Аналогично определим номера остальных членов ряда параметра D :
NV 2=20+2 × 16-24+28=56;
NV 3=20+2 × 32-24+28=88;
NV 4=20+2 × 48-24+28=120;
Номеру 24 соответствует число 4, остальным номерам соответствуют значения параметров объема резервуара 25; 160; 1000 м3 .
Пример 3. Определить известные показатели уровня унификации для изделия весом 6 кг, состоящего из 120 деталей, 90 из которых, весом 5,4 кг, унифицированы.
Решение:
Количество и вес деталей заданы, исходя из этого определим показатели уровня унификации по количеству и весу деталей:
УД=(КУ/КД) × 100%=(90/120)×100%=75%;
УВ=(ВУ/ВО) × 100%=(5,4/6)×100%=90%.
Пример 4. Определите показатели уровня унификации, если известно, что на изготовление изделия, состоящего из 100 деталей, 80 из которых унифицированы, двое рабочих затратили три дня.
Решение:
Определим уровень унификации по количеству деталей:
УД=(80/100) × 100%=80%
Затем рассчитаем суммарную трудоемкость изготовления всего изделия чел.-дн.:
ТП=3 ×2=6
Суммарная трудоемкость изготовления одной детали, чел.-дн.:
ТП1=ТП/100=6/100=0,06
Суммарная трудоемкость изготовления унифицированных деталей:
УТ=(ТС/ТП) × 100%=4,8/6 × 100%=80%
Задача 4.1
Определить показатели унификации, если известно, что на изготовление изделий общим весом ВО, состоящего из КД деталей, из которых КУ унифицировано, общим весом ВУ, затрачено ТП чел.дней, причем трудоемкость изготовления унифицированных деталей равна СУ. Средняя стоимость нормо-часа Р рублей (таблица 4.1).
Задача 4.2
Определить ряды параметра Z (таблица 4.2), если зависимость между Z и K определяется выражениями, а также известен ряд, по которому задан параметр К.
Z = AK 2 / BC (1), Z = ABC / K 2 (2), Z = AK 3 / BC (3),
Z = A ВСК (4), Z = AB/CK (5), Z=AB / CK3 (6),
Задача 4.3
Рассчитайте N значений линейного параметра в области от В1 до В2 по геометрической прогрессии и проведите нормализацию этого параметра (таблица 4.3). Определите ряд предпочтительных чисел, которому будут соответствовать рассчитанные значения параметра.
Таблица 4.1
| № | КД | КУ | ВО | ВУ | ТП | ТС | СД | СУ | Р |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | 534 1264 826 98 41 386 482 824 683 741 128 186 473 289 146 947 401 672 258 369 147 789 456 123 741 852 963 401 520 306 402 259 370 150 780 451 122 739 847 952 | 287 879 231 89 21 264 246 426 452 301 89 123 305 164 78 689 236 102 187 264 123 654 321 102 645 654 357 246 439 208 250 180 263 120 644 319 100 635 650 347 | 48 126 86 67 55 1154 246 287 1468 862 98 32 466 555 801 100 364 52 1423 158 295 145 439 89 123 305 164 78 689 236 360 1400 146 420 88 133 300 154 72 679 | 26 117 61 23 32 521 143 189 1023 457 36 19 300 333 521 42 213 31 862 36 200 75 246 46 39 124 106 36 409 154 210 860 35 183 74 241 45 35 135 102 | 10 13 8 6 7 24 15 41 53 32 64 16 20 13 9 42 28 31 88 24 16 18 19 24 31 26 41 26 31 21 24 85 17 18 22 30 24 40 25 30 | 3 8 5 2 3 18 6 19 26 12 24 7 10 3 5 24 18 16 57 11 9 6 7 10 11 12 19 13 14 8 17 50 9 6 10 12 11 18 12 14 | 4,3 6,5 11,3 1,8 2,7 7,8 8,9 18,7 21,4 16,4 19,2 5,6 11,1 13,6 3,8 8,1 8,4 7,2 14,3 4,8 16,7 21,6 12,5 8,4 7,5 9,6 4,2 5,8 9,4 7,6 8,6 13,9 4,7 16,3 20,5 12,4 8,2 7,1 9,2 4,1 | 3,8 6,5 10,6 1,3 2,1 6,4 7,8 9,8 15,3 14,4 16,5 4,7 10,1 12,5 3,2 7,2 7,5 4,6 11,6 4,7 10,3 20,3 9,8 7,2 6,6 5,2 4,0 5,5 9,1 5,6 7,2 10,9 4,6 10,3 19,5 8,8 7,0 6,4 5,0 3,9 | 4,2 2,9 3,7 5,1 4,3 5,9 4,9 7,9 23,5 24,4 14,1 3,8 9,6 11,4 13,6 6,3 6,6 3,8 15,8 6,5 9,6 13,5 12,3 5,6 7,8 10,4 2,1 5,2 6,2 8,6 5,0 15,6 6,5 9,2 12,9 5,8 7,1 10,2 2,0 1,9 |
Таблица 4.2
| № | Z | Ряд | К | А | В | С |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 | R5/2 R10/2 R10/3 R20/2 R20/3 R20/4 R40/2 R40/3 R40/4 R40/5 R5/2 R10/2 R10/3 R20/2 R20/3 R20/4 R40/2 R40/3 R40/4 R40/5 R5/2 R10/2 R10/3 R20/2 R20/3 R20/4 R40/2 R40/3 R40/4 R40/5 R5/2 R10/2 R10/3 R20/2 R20/3 R20/4 R40/2 R40/3 R40/4 R40/5 | (2,5...1600) (0,02...0,25) (1,6...80) (14...71) (22,4...90) (6,3...45) (1,32...4,25) (2,12...10) (5...10) (850...3550) (40...400) (2...31,6) (31,5...1000) (0,71...2,5) (0,9...2,5) (35,5...224) (1,32...3) (1,06...2,36) (1,18...2,36) (2,8...9) (2,5...100) (0,2...2,5) (0,16...8) (1,4...7,1) (2,24...9) (0,63...450) (0,132...425) (21,2...100) (0,5...1,0) (8,5...355) (4...40) (20...316) (3,15...100) (7,1...25) (9...25) (3,55...22,4) (13,2...30) (10,6...23,6) (11,8...23,6) (0,28...0,9) | 0,213 6,3 0,281 0,794 50,12 179,2 0,355 12,56 14,1 2,114 0,159 5,01 0,199 22,39 35,49 0,178 501,1 15,93 8,427 4,482 0,213 6,3 0,281 0,794 50,12 179,2 0,355 12,56 14,7 2,114 0,159 5,01 0,199 22,39 35,49 0,178 501,1 15,93 8,427 4,482 | 7,08 25,1 3,54 0,22 5,96 281 0,53 2,99 25,1 0,02 63,0 71,0 3,16 1,78 1,32 0,56 0,02 3,55 0,53 0,16 7,08 25,1 3,54 0,22 5,96 281 0,53 2,99 25,1 0,02 63,0 71,0 3,16 1,78 1,32 0,56 0,02 3,55 0,53 0,16 | 3,16 3,98 8,91 0,11 1,26 0,5 1,18 5,3 0,53 0,14 0,25 0,25 56,2 8,92 7,1 0,15 3,01 6 0,18 1,71 3,16 3,98 8,91 0,11 1,26 0,5 1,18 5,3 0,53 0,14 0,25 0,25 56,2 8,92 7,1 0,15 3,01 6 0,18 1,71 |
Таблица 4.3
| № | N | В1 | В2 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | 14 10 12 8 7 9 11 6 10 13 14 10 12 8 7 9 11 6 10 13 14 10 12 8 7 9 11 6 10 13 14 10 12 8 7 9 11 6 10 13 | 0,133 50,1 631 12,57 0,04 28,05 5,31 0,159 21,2 0,944 1,33 501 63,1 125,7 0,4 280,5 53,1 0,0159 212 9,44 13,3 5,01 6,31 1,257 4 2,805 0,531 2,12 94,4 0,0133 0,501 0,631 0,1257 40 0,2805 531 1,590 0,212 0,0944 133 | 1,497 398 158490 400,00 0,46 162,00 22,38 39,811 66,8 4,230 14,97 3981 15849 4000,0 4,6 1620,0 223,8 3,9811 668 42,3 149,7 39,81 1584,9 40,000 46 16,200 2,238 6,68 423,0 0,1497 3,981 158,49 4,0000 460 1,6200 2238 398,11 0,668 0,4230 1497 |
Таблица 4.4 Основных ряды предпочтительных чисел
| Номер | R5 | R10 | R20 | R40 |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | 1,00 1,60 2,50 4,00 6,30 | 1,00 1,25 1,60 2,00 2,50 3,15 4,00 5,00 6,30 8,00 | 1,00 1,12 1,25 1,40 1,60 1,80 2,00 2,24 2,50 2,80 3,15 3,55 4,00 4,50 5,00 5,60 6,30 7,10 8,00 9,00 | 1,00 1,06 1,12 1,18 1,25 1,32 1,40 1,50 1,60 1,70 1,80 1,90 2,00 2,12 2,24 2,36 2,50 2,65 2,80 3,00 3,15 3,35 3,55 3,75 4,00 4,25 4,50 4,75 5,0 5,30 5,60 6,00 6,30 6,70 7,10 7,50 8,00 8,50 9,00 9,50 |
Дата: 2019-02-02, просмотров: 275.
