Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Ремонтопригодность-свойство элемента ЭС (объекта), заключающееся в его приспособленности к предупреждению, обнаружению и устранению отказов и неисправности путём проведения технического обслуживания и ремонтов. Её количественные показатели- случайные величины, определяемые с помощью математического аппарата ТВ , МС и теории массового обслуживания.

Единичные показатели:

1. Среднее время восстановления-М[t_в]-математическое ожидание времени восстановления работоспособности объекта. При известном законе распределения:

 

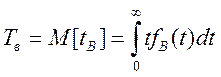                 ,                                               (3.123)

 

где

f_в(t)-плотность распределения времени восстановления.

 

По статическим данным:

 

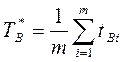                 ,                                                                       (3.124)

где

t_вi-время устранения i-го отказа ;

m-число отказов в процессе эксплуатации или испытаний.

2. Характеристики рассеяния:

 

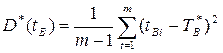                 ;                                              (3.125)

 

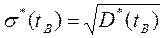.                                                             (3.126)

 

3.Вероятность восстановления объекта в заданное время”t”:

 

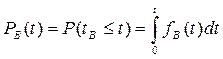                                                                (3.127)

 

Статистическая оценка показателя:

 

                 P_в^*(t)=1-n(t)/N(t),                                                                (3.128)

 

где

n(t)-число изделий не восстановленных за промежуток времени t

(t)-число изделий подлежащих восстановлению за промежуток времени t

Для определения величины P_в(t) надо знать закон распределения времени восстановления

4. Интенсивность восстановления – вероятность восстановления работоспособности объекта в единицу времени при условии , что до него восстановления не было.

 

                 m(t)=f_в(t)/(1-F_B(t))                                                                          (3.129)

 

где

F_в(t)-функция распределения времени восстановления.

       Статистическая оценка интенсивности восстановления:

 

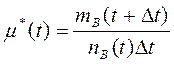                                                                             (3.130)

 

где

Dt-рассматриваемый промежуток времени ;

m_в(t+Dt)-число восстановлений в интервале времени от t до t+Dt;

n_в(t)-число не восстановленных изделий на момент времени t

 

                 m(t)=1/T_B         m^* (t)=1/T^*_B                                            (3.131)

 

Для наиболее распространённого экспоненциального закона:

 

                 P_в(t)=1-е^mt=1-e^-t/T_в         P_в(t)=1-е^mt=1-e^-1/T_в                    (3.132)

 

Число отказов , которое может быть устранено за время «t”:

 

                 m=lT(1-e^-mt)                                                                       (3.133)

 

где

l-интенсивность отказов ,T-время эксплуатации.

 

Если “k” –среднее число восстановлений за заданное время t,

 

                             К=mt                                                                                   (3.134)

 

то для определения вероятности “m” восстановлений используем закон Пуассона:

 

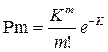                                                                                             (3.135)

 

При к<1:

 

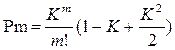                                                                            (3.136)

 

5.Улучшение ремонтопригодности зависит от показателей надёжности m,l,t,T. При экспоненциальном законе распределения отказов и их восстановления :

 

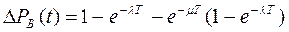                                                (3.137)

 

Уравнение определяет какая вероятность общего числа отказов за время эксплуатации , которое м.б. устранено за время “t”

 

                 Комплексные показатели ремонтопригодности

1) Коэффициент готовности для не резервированной системы

 

            К_г=T₀/ T₀+ T_B                                                                     (3.138)

 

где

Tо –наработка на отказ;

T_в –среднее время восстановления отказа

 

                 К_г=m/(l+m)                                                                                 (3.139)

 

                 m=1/ T_B; l=1/ T₀                                                                (3.140)

 

2) Коэффициент ремонта (простоя) для не резервированной системы:

 

                 К_р=Tp/(T+Tp)                                                                    (3.141)

 

или

                 К_р=l/(l+m)                                                                                (3.142)

 

где

Т_р- время ремонта;

Т- рабочее время (время эксплуатации)

 

Эти коэффициенты (К_г,К_р) для начального периода эксплуатации , когда вероятность безотказной работы выше , чем в конце , с учётом экспоненциального закона появления и восстановления отказов:

 

                 К_г=m/(l+m)+l/Т(l+m)-lexp[-(l+m)T]/Т(l+m)²,           (3.143)

 

                 К_P=l/(l+m)-l/Т(l+m)+lexp[-(l+m)T]/Т(l+m)².           (3.144)

 

3) Для резервированной системы при экспоненциальном законе восстановления отказов и установившемся процессе :

 

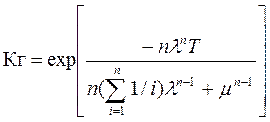                             ,                       (3.145)

 

где

n-число резервных элементов.

 

Когда допускается предельное время обслуживания - “t” :

 

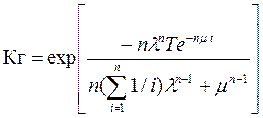                             .                        (3.146)

 

Таким образом система работоспособна, если один из её элементов может быть восстановлен до нормального режима работы в течении времени “t”.

4) Коэффициент технического использования :

 

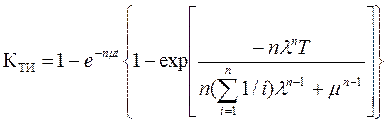                       (3.147)