Для оценки надежности восстанавливаемых, т.е. ремонтопригодных элементов (объектов, систем), используются следующие показатели надежности.
1. Вероятность восстановления (функция распределения времени восстановления – Fв)S(t) - вероятность того, что отказавшее изделие будет восстановлено в течение заданного времени ”t”, т.е. вероятность своевременного завершения ремонта.
Очевидно, что 0£S(t)£1, S(0)=0, S(¥)=1.
Для определения величины S(t) используется следующая статистическая оценка:
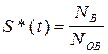, (3.50)
где
NОВ - число изделий, поставленных на восстановление;
NВ - число изделий, время восстановления которых было меньше заданного времени ”t”.
2. Вероятность несвоевременного завершения ремонта (невосстановления) G(t) - вероятность того, что отказавшее изделие не будет восстановлено в течение заданного времени t.
Статистическая оценка величины G(t):
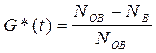, (3.51)
Из анализа выражений (3.50) и (3.51) следует, что:
S(t) + G(t) = 1. (3.52)
3. Частота восстановления,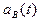 
- плотность распределения времени восстановления - определяется по формуле:
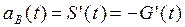(3.53)
Статистическая оценка величины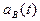 
:
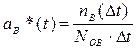, (3.54)
где
NOB - число изделий, поставленных на восстановление;
nВ(Dt) - число восстановленных элементов на интервале времени (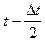 
, 
).
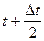4. Интенсивность восстановления m(t) - условная плотность распределения времени восстановления для момента времени ”t” при условии, что до этого момента восстановление изделия не произошло:
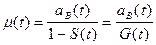, (3.55)
Статистическая оценка величины m(t):
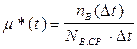, (3.56)
где
NB.CP. - среднее число изделий, которые не были восстановлены в интервале времени (0, t).
nВ (Dt) - число восстановленных изделий за интервал t.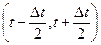 
В отличие от процесса отказов, развивающихся во времени естественным образом, процесс восстановления является целиком искусственным и полностью определяется организационно-технической деятельностью эксплуатационно-ремонтного персонала.
Поэтому кривая интенсивности восстановления, аналогичная кривой интенсивности отказов отсутствует. Так как существуют нормативы времени на проведение ремонтных работ, то m(t) = m = const и численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов. При постоянстве во времени величины «m» получаем экспоненциальное распределение для времени восстановления:
, 
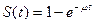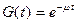(3.57)
5. Среднее время восстановления (ТВ) представляет собой математическое ожидание времени восстановления:
; 
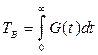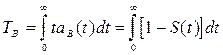; (3.58)
Статистическая оценка времени восстановления находится из выражения:
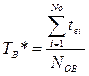; (3.59)
где
tвi - время восстановления i-го элемента;
NOB – количество изделий, поставленных на восстановление.
При m = const имеем:
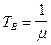. (3.60)
Среднее время восстановления включает продолжительность послеаварийного ремонта ТАВ и продолжительность планового ремонта ТПЛ:
ТВ = ТАВ + ТПЛ . (3.61)
Статистическая оценка этой величины определяется из выражения:
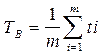, (3.62)
где
m - количество отказов;
ti – время восстановления одного отказа.
Время восстановления - среднее время вынужденного простоя, необходимое для отыскания и устранения одного отказа.
Время восстановления как правило подчиняется не экспоненциальному закону - чаще это нормальное распределение, распределение Вейбулла или Пуассона. Анализ систем с неэкспоненциальным распределением чрезвычайно сложен и практически его расчетная формула не поддается формализации.
В то же время замена реального закона распределения экспоненциальным с тем же математическим ожиданием мало искажает конечные результаты. Поэтому во многих случаях эта замена обоснована. При этом:
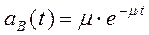, (3.63)
где
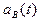- частота восстановления;
m - интенсивность восстановления, m(t) = m = const.
Вероятность восстановления:
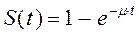. (3.64)
Среднее время восстановления:
. (3.65)
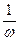6. Поток отказов w(t) - математическое ожидание числа отказов элементов, происшедшее за единицу времени, при условии, что отказавшие элементы заменяются новыми, т.е. число испытываемых элементов сохраняется одинаковым в процессе эксплуатации.
Величина - средняя наработка на отказ.
Параметр потока отказов восстанавливаемого элемента - w(t) - среднее количество отказов элемента в единицу времени, удельная повреждаемость элемента.
По данным эксплуатации из статистической модели имеем:
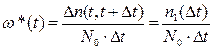, (3.66)
где
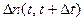, n1(Dt) - количество элементов, отказавших за интервал времени Dt или 
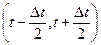при условии, что отказавшее изделие немедленно заменяется новым;
N0 - число элементов на испытании, при условии замены отказавших элементов.
;
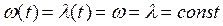Среднее время наработки на отказ:
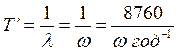. (3.67)
Если w(t) - последовательность случайных моментов отказа восстанавливаемой системы, образует поток отказов, то временная последовательность состояний объекта (износ, отказ, восстановление, работа и т.д.) образуют переменный (алтернирующий) процесс восстановления. Если длительность состояний описывается экспоненциальным законом распределения, то процесс считается простейшим пуассоновским. Для него характерны свойства стационарности, ординарности и отсутствия последействия.
а) Поток отказав - стационарный, если вероятность появления того или иного числа отказов на заданном отрезке времени зависит только от его длины и не зависит от того, где он находится.
б) Поток отказов - ординарный, если вероятность появления двух и более отказов на малом отрезке времени - пренебрежимо мала по сравнению с появлением одного отказа.
в) Поток отказов - поток без последействия, если вероятность появления числа отказов на некотором отрезке времени не зависит от числа и характера отказов, возникших до этого отрезка времени.
Таким образом w(t) - последовательность отказов элемента во времени, характеризуемая параметром потока отказов - «w», который является аналогом «l».
Для ординарных потоков эти понятия совпадают, но «w» и «l» имеют разную природу. Поток отказов (w) - безусловная вероятность отказа элемента за единицу времени. Интенсивность отказов (l) - условная вероятность отказа элемента за единицу времени, при условии, что он проработал до момента «t».
На рис 3.4 представлена графическая зависимость потока отказов в функции времени.
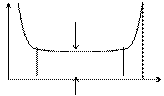w(t) Из рис 3.4 видно, что: 
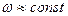в период
нормальной работы, что говорит о том, что отказы
системы возникают
примерно через одинаковые промежутки времени,
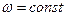равные ее наработке на отказ (рис3.4).
0 t1 t2 t3 t
Рис 3.4
На рис 3.4 имеем интервал времени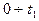 
- приработочные дефекты изготовления и монтажа элемента ЭС, например, для ЛЭП это время составляет 1-3 года;
интервал времени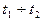 
- нормальная работа элемента ЭС;
интервал времени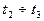 
- износ изделия.
Вероятность возникновения «m» отказов за время «t» при частоте отказов «w» в пуассоновском потоке событий (отказ, восстановление, т.е. ординарном, стационарном, без последействия) вычисляются по формуле:
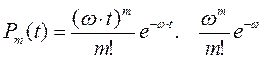. (3.68)
При длительности периода работы элемента ЭС t=1 году.
или
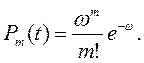(3.69)
где
m – число восстановлений (число отказов) в рассматриваемом интервале времени.
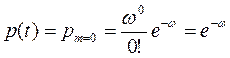Вероятность безотказной работы элемента:
(3.70)
- это вероятность того, что за год не будет ни одного отказа элемента.
Дата: 2019-02-02, просмотров: 297.
