Предполагая , что отказы ЛЭП и электрических сетей – независимы получим основные формулы для расчёта надёжности комбинации двух элементов.
1. Если р1 – надёжность одного элемента , р2-другого, то вероятность того, что оба будут работать безотказно в течении времени “t”:
(4.30)
где
l1, l2-интенсивности отказов элементов , которые м.б. постоянными или переменными во времени;
р1, р2 – вероятность отказов элементов ЛЭП.
2. Вероятность того , что один или оба элемента откажут :
qпосл(t)=q1(t)+q2(t)-q1(t)+q2(t)=1-P1(t)+1-P2(t)-[1-P1(t)][1-P2(t)]=
=1-P1(t)P2(t)=1-Pпосл(t), (4.31)
где
q1, q2 – вероятность отказов элементов ЛЭП.
3. Вероятность того , что будут работать один или два элемента:
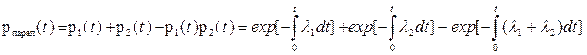(4.32)
4.Вероятность , что откажут оба элемента ЛЭП:
qпарал(t)=q1(t)q2(t)=[1-р1(t)][1-р2(t)]=1-р1(t)-р2(t)+р1(t)р2(t)=1-рпарал(t) (4.33)
Случаи 1 и 2 – представляют противоположные события т.е. рпосл+qпосл=1 , поскольку противоположные события для безотказной работы двух элементов осуществляется тремя путями : отказывает один из элементов , либо оба вместе. Следовательно, величины «рпосл» и «qпосл» можно соответственно назвать надёжностью и ненадёжностью последовательного соединения элементов или последовательной системы .Это означает , что отказ любого элемента , приводит к отказу системы .Случаи 3 и 4 –противоположные события т.е. рпарал+qпарал=1 , т.к. противоположные события для двух отказавших систем – события , когда один или оба элемента работают безотказно. Величины «рпарал» и «qпарал» называются соответственно надёжностью и ненадёжностью параллельного соединения элементов или системы с постоянным резервом .Это означает , что если один элемент отказал, то существует другой элемент , который выполняет требуемую функцию .Параллельная система из двух элементов не отказывает при отказе одного элемента , если оставшийся удовлетворительно выполняет требуемую функцию .
Приведённые формулы используются при экспоненциальном и неэкспоненциальном распределении отказов элементов .В первом случае они упрощаются
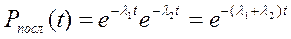; (4.34)
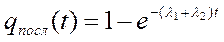; (4.35)
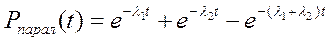; (4.36)
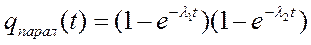. (4.37)
ЛЭП и электрические сети обычно состоят из большого числа соединённых последовательно элементов или блоков .В некоторых случаях к заведомо малонадёжным элементам ЛЭП для повышения надёжности подключаются резервные элементы , иногда к целым группам элементов подключаются такие или же подобные группы , включаемые параллельно (например групповое включения вентилей на п/ст ЛЭП постоянного тока).Такие параллельные соединения можно рассматривать как блоки , соединённые последовательно .Система отказывает , если отказывает такой блок в целом .
Для «n» элементов или блоков , соединённых последовательно , надёжность системы выражается формулой :
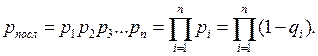- (4.38)
Выражение (4.38) представляет закон произведения надёжности,
где
рi-надёжность i- го элемента или блока в последовательном соединении.
Надёжность ЛЭП с параллельно соединёнными элементами .
Если имеется структурная схема надёжности с последовательным соединением элементов, когда отказ 1-го элемента вызывает отказ 2-го, затем 3-го и т.д., то имеем схему с последовательным соединением зависимых элементов (рис 4.3)
    P1
| P2 | Pn |
Рис 4.3
В этом случае, если «А» - событие заключающееся в том, что система работает безотказно, а «Аi»(i=1,2….n) – события состоящие в исправной работе элементов системы, то событие «А» имеет место, если имеют место события «Аi». Надёжность системы:
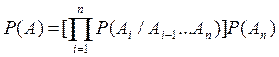. (4.39)
Однако на практике отказ любого элемента – отказ системы. Вероятность безотказной работы, в этом случае, произведение вероятностей для независимых событий :
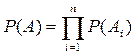. (4.40)
Так как произведение величин «q» есть намного меньше от сумм этих величин для отдельных элементов
>> 
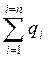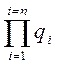(4.41)
В упрощённых расчётах, для схемы с последовательным соединением элементов, можно принять:
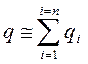(4.42)
Ошибка при этом упрощении не превышает несколько процентов. Коэффициент отказа (аварийности) «q» обычно для ЛЭП имеет величину: q £ 0.01.
4.4. Надёжность ЛЭП с параллельным соединением элементов.
Для определения оптимальной надёжности ЛЭП и электрических сетей на стадии их проектирования приходится иногда дублировать отдельные элементы или цепи – использовать резервирование .На практике используют нагруженный (постоянно включённый) и не нагруженный (холодный) резервы. В последнем случае , когда работает элемент (цепь) имеется один или более резервных элементов (цепей) , которые могут вступать в действия при отказе основного рассмотрим надёжность ЛЭП при нагруженном резерве.
Имеем для 2-х элементов: вероятность того, что будут работать один или два элемента:
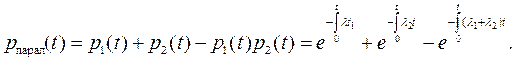(4.43)
Вероятность , что откажут 2-а элемента:
qпарал(t)=q1(t)q2(t)=[1-p1(t)][1-p2(t)]=1-p1(t)-p2(t)+p1(t)p2(t)=1-pпарал(t). (4.44)
Формулы (4.43) и (4.44) – представлены в пункте 4.3 предыдущей темы.
В экспоненциальном случае:
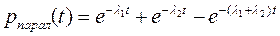; (4.45)
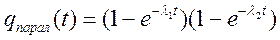. (4.46)
Обобщим эти формулы для общего случая:
Сформулируем правило для вычисления вероятности того , что из трёх событий А , В , С , имеющих вероятности P(А) , Р(В) , Р(С) выполняются либо А , либо В , либо С , либо любая комбинация этих трёх событий .Это правило запишется в виде :
P(A+B+C)=P(A)+P(B)+P(C)-P(A)P(B)-P(A)P(C)-P(B)P(C)+P(A)P(B)P(C). (4.47)
Если события имеют одинаковую вероятность:
P(A)=P(B)=P(C)=P, (4.48)
то
P(A+B+C)=3P-3P2+P3. (4.49)
Аналогично можно иметь формулы для четырёх и более событий .
Используя выражение (4.47) можно определить надёжность для трёх параллельно соединённых элементов , как вероятность того , что хотя бы один из элементов будет исправен:
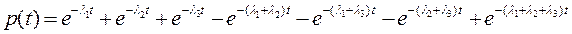.(4.50)
Если 
:
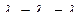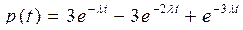. (4.51)
Аналогично определяется надёжность работы 4-х и более параллельных элементов.
Более просто определить величину «q(t)» , а потом значение р(t)=1-q(t) .
Вероятность отказа 2-х элементов q=q1q2 ;3-х q=q1q2q3 а “n” элементов:
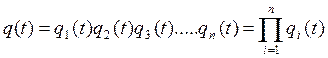(4.52)
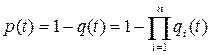(4.53)
Если работающие параллельно элементы одинаковы по вероятности отказа, то:
qпар=qn ; рпар=1-qn. (4.54)
Для параллельной работы группы элементов :
рпар=1-qпар=1-qn=1-(1-р)n, (4.55)
где
р - надёжность 1-го элемента, т.е. вероятность безотказной работы.
Если параллельно соединить “n” групп элементов , в каждой из которых “m” элементов работает последовательно (рис 4.4), то :
р1 рi
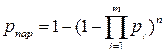(4.56)
n
Рис.4.4
Надёжность одной цепи из m последовательных элементов из которых “в” элементов дублированы (рис 4.5):
Рис 4.5
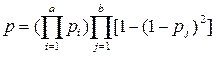, (4.57)
где
Pj – надёжность i-го не резервированного элемента;
Pj – надёжность j-го резервированного элемента;
а – число не дублированных элементов (а = m = в);
m – число последовательно соединённых элементов;
в – количество элементов дублированное из «m».
Надёжность системы из двух параллельных цепей (рис 4.6):
р
р
Рис.4.6
рпар=1-(1-р)2. (4.58)
где
р – надёжность одной линии
Дата: 2019-02-02, просмотров: 245.
