Показателями надежности называют количественные характеристики одного или нескольких свойств электрической системы (ЭС) составляющих ее надежность.
К таким характеристикам относят, например, временные понятия - наработку элемента электрической системы до отказа, наработку между отказами, срок службы, время восстановления.
Значения этих показателей получают по результатам испытаний или эксплуатации.
По восстанавливаемости элементов ЭС показатели надежности подразделяют на показатели для восстанавливаемых изделий и показатели для невосстанавливаемых изделий. Применяются также комплексные показатели. Надежность элементов электрической системы можно оценивать, используя часть показателей надежности, либо все показатели.
Основные показатели безотказности:
§ вероятность безотказной работы P(t) - вероятность того, что в пределах заданной наработки отказ ЭС или ее элемента не возникают;
§ среднее время безотказной работы (средняя наработка до отказа) (T) - математическое ожидание наработки ЭС или ее элемента до первого отказа;
§ средняя наработка на отказ (t, tср) - отношение суммарной наработки восстанавливаемого элемента ЭС к математическому ожиданию числа его отказов;
§ интенсивность отказов (l) - условная плотность вероятности возникновения отказа элемента ЭС, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Этот показатель относится к невосстанавливаемым элементам ЭС.
С учетом материала по математическим основам надежности изложенного в курсе «Математические основы энергетики» рассмотрим табл.3.1 функциональную связь между основными показателями надежности: P(t), F(t), f(t), l(t), t, т.е. вероятностью безотказной работы; функции распределения (вероятностного отказа - «q»), плотностью распределения наработки до отказа, интенсивностью отказов и средней наработки до отказа.
В табл.3.2 указанные величины представлены для основных законов распределения случайной величины (СВ).
Здесь:
a - вид плотности распределения;
k - масштаб распределения СВ;
«Г» - гамма функция.
Рассмотрим более детально основные показатели (параметры) надежности:
1. Вероятность безотказной работы P(t)=R(t) - вероятность того, что в заданном интервале времени не произойдет отказ
P(t)=1-q(t); 0£P(t) £1; P(0)=1; P(¥)=0;
С другой стороны: P(t)=1-F(t);
F(t)=q(t) - вероятность появления отказа в течении времени «t»;
P(t) – монотонно убывающая функция;
F(t)- монотонно возрастающая функция;
Статистическая оценка:
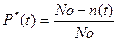(3.1)
где
No - общее количество элементов для испытания или эксплуатируемых;
n(t) - число элементов, отказавших за время «t»;
P(t) - вероятность безотказной работы.
Безотказность - свойство системы сохранять работоспособность в течение заданного интервала времени без вынужденных перерывов. Если «tр» - время безотказной работы, то P(t)=P(tp>t) - вероятность того, что время безотказной работы > t. Зависимость P(t) - закон распределения надежности.
2. На практике более удобная характеристика - вероятность отказов (вероятность неисправной работы).
Эта характеристика более удобна ,в частности , для сравнения резервируемых и нерезервируемых ЛЭП и т.п.
Исправная работа и отказ - несовместимые и противоположные события.
q(t)=1-P(t)=F(t) (3.2)
где
q(t) – функция распределения времени безотказной работы , представляющая вероятность появления отказа в течении времени”t” .
Подставляя формулу (3.2) в (3.1) имеем:
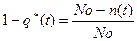, откуда 
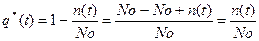(3.3)
где
q(t) - вероятность отказа. Отказ - нарушение работоспособности (способности системы выполнять заданные функции с требуемыми режимными параметрами). q(t)- вероятность того, что в заданном интервале времени произойдет хотя бы один отказ:
q(t)=q(tp<t),
При этом , если t=var (переменная величина) от 0 до ¥, то имеем q(t)=var от 0 до 1.
Для восстанавливаемых (ремонтируемых) элементов представляет интерес вероятность отказа за длительный период наблюдения qср(¥), эту величину называют также коэффициентом вынужденного простоя (Кв) – этот коэффициент характеризует время вынужденных простоев за год, и измеряется в относительных единицах. Одновременно можно записать:
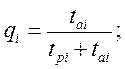
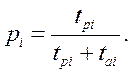(3.4)
Эти выражения (3.4) также подходят для восстанавливаемого элемента ЭС. В этом случае:
Ti=tpi+tai - время наблюдения за элементом «i»;
tai - время аварий элемента «i»;
tpi – время безотказной работы “iго“ элемента.
tai=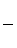 
,
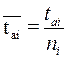где
ni- число аварий “iго” элемента;
tai- среднее время. аварии;
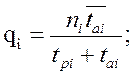
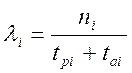, (3.5)
где qi(t)-функция , определяющая распределение вероятности повреждения(отказа) элемента “i” во времени
lI(t)-надёжность работы “i”элемента в часовом пределе(t1,t2):
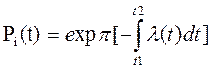. (3.6)
Интегральная функция распределения вероятностей отказа:
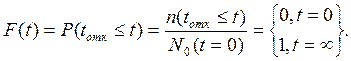(3.7)
Эта функция (3.7) численно равна доле начального количества объектов N0(t=0), отказавших до произвольного, но фиксированного момента времени "t", что составляет n(tотк£t) объектов.
Для этого случая, вероятность безотказной работы:
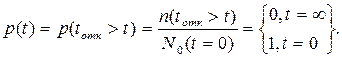(3.8)
Таким образом интегральная функция распределения вероятностей безотказной работы p(t) численно равна доле начального количества объектов N0(t=0) , не отказавших до произвольного, но фиксированного момента времени "t" это n(tотк>t) объектов.
Графически имеем для "i" объекта (элемента)
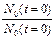
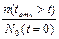
p(t)
1 Область возможного
изменения p(t)
t
0 t
tотк £ t tотк>t
Рис 3.1
На рис. 3.2 представлена графическая зависимомть интегральной функци распределения вероятностей отказа
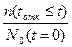
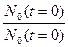
F(t)
1
Область возможного
изменения F(t)
0 t
tотк £ t tотк>t
Рис 3.2.
Из приведенных формул (3.7) и (3.8) и рис.3.1 и 3.2 видно, что
n(tотк>t) = N(t=0)- n(tотк£t); n(tотк£t) = N(t=0) - n(tотк>t). (3.9)
Следовательно:
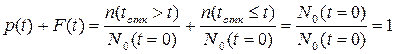(3.10)
Для произвольного момента времени 0 £ t £ ¥, таким образом вероятность безотказной работы объекта в течении времени t и вероятность его отказа до момента t образуют полную группу несовместимых событий
p(t)+F(t)=1, p(t)=1- F(t), F(t)=1- p(t). (3.11)
3. Среднее время безотказной работы или средняя наработка до отказа (t, Тср,Tо) - математическое ожидание случайной. величины времени безотказной работы элемента до первого отказа:т.е. математическое ожидание наработки до первого отказа
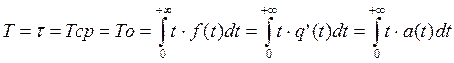, (3.12)
где
f(t)=a(t) - плотность распределения наработки до отказа, частота отказов;
Это выражение (3.12) путём интегрирования по частям может быть преобразовано следующим образом :
T=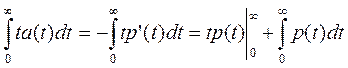 
(3.13)
Учитывая ,что t ³0, р(0)=1 и р(¥)=0,окончательно получаем:
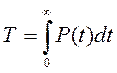(3.14)
Для экспоненциального закона распределения времени безотказной работы имеем :
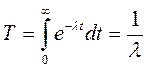. (l=const) (3.15)
Таким образом, среднее время наработки элемента(объекта) на отказ численно равно средней , по множеству объектов , продолжительности безотказной работы (между двумя соседними отказами ) , приходящейся на один элемент (объект) , т.к. l(t)=const , то и T=const т.е. эти величины могут быть вычислены для всех элементов ЭС и сведены в таблицы , остальные показатели надёжности определяются через эти величины.
По статистическим данным среднее время наработки элемента ЭС до отказа определяется из выражения:
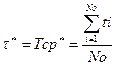, (3.16)
где
ti- время безотказной работы i-го элемента ЭС;
No - общее число элементов взятых для испытания.
В выражение (3.16) необходимо знать момент выхода из строя каждого элемента. Более удобная форма записи :
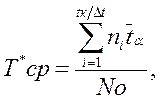(3.17)
где
ni - число элементов, отказавших в i-ом интервале;
tк - время в течение которого отказало "Nо" элементов;
Dt - выбранная величина интервала времени.
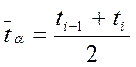- среднее время i-го интервала; (3.18)
где
ti-1 - время в начале i-го интервала;
ti - время в конце i-го интервала;
С другой стороны, имеем:
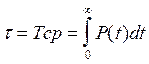(3.19)
4. Интенсивность отказов (l). Эта величина представляет собой вероятность отказа неремонтируемого изделия в еденицу времени после данного момента времени при условии, что отказ до этого момента не возник . Численно она равна среднему числу отказов в единицу времени на один объект из количества объектов n(tотк>t) не отказавших до произвольного, но фиксированного времени "t".
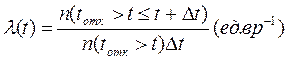(3.20)
Понятие интенсивность отказов устройства в единицу времени используется как количественная характеристика для математического определения надёжности. Эта величина измеряется в среднем обычно числом отказов за один час. Обратная величина "l" - наработка до первого отказа в часах - отношение общего времени испытания к общему числу отказов. В литературе часто встречается следующее определение интенсивности отказов : это условная плотность распределения времени безотказной работы для момента времени t при условии, что до этого момент отказа не произошел. (интенсивность появления отказов в единицу времени)
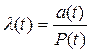, т.к. P(t) £ 1, то l(t) ³ а(t); (3.21)
где
Р(t) – вероятность безотказной работы элемента ЭС
а(t) - частота отказов элемента ЭС.
Со статистической точки зрения интенсивность отказов l(t) - отношение числа отказавших элементов ЭС за некоторый промежуток времени к числу работоспособных элементов в начале этого промежутка.
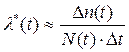(3.22)
или
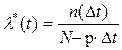, (3.23)
где
Dt - интервал времени;
Dn(t) - число элементов, отказавших за Dt;
n(Dt) - число элементов отказавших в интервале от (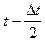 
) до ( 
);
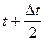N(t) - число элементов, исправно работающих к началу промежутка времени.
Nср=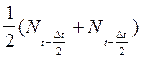 
- среднее число исправно работающих элементов в интервале Dt.
Покажем справедливость этой оценки. Учитывая ,что Nср=Nо-n(t),получим :
n(t)-число изделий ,отказавших в течении времени "t";
n(Dt)-число изделий (элементов) отказавших в течение времени" Dt"
n(Dt)=[N(t+ Dt)-N(t)],где
N(t) и N(t+ Dt)-число изделий (элементов) безотказно проработавших в течении времени t и t+Dt соответственно.
При достаточно большом числе изделий (элементов) ,поставленных на испытание (эксплуатации),можно записать:
N(t)=NоP(t); (3.24)
N(t+Dt)=NоP(t+Dt) (3.25)
Отсюда:
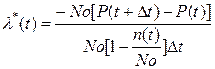(3.26)
При достаточно большом «Nо» можно записать:
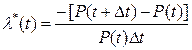(3.27)
При Dt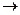 
0 получим :
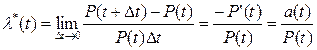(3.28)
Для высоконадёжных систем если P(t)=0.99,то как следует из формулы (3.25): а(t)»l(t)
Ошибка не более 1% и не превышает ошибок статистического определения а(t) и l(t).
Следует подчёркнуть разницу между величинами а(t) и l(t) .Вероятность а(t)dt характеризует вероятность отказа системы (элемента) за интервал времени (t,t+Dt),взятой(го) произвольным образом из группы систем (элементов) ,причём неизвестно в каком состоянии (работоспособным или неработоспособным) находится система(элемент).Вероятность l(t)dt характеризует вероятность отказа системы(элемента) за интервал (t,t+Dt),взятую(го) из группы систем(элементов),которые остались работоспособными моменту времени “t”
Интегрируя выражение (3.25) l(t)=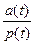 
,имеем :
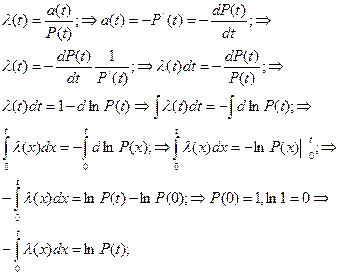
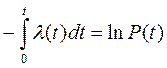или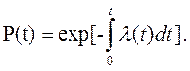 
(3.29)
Так как:
l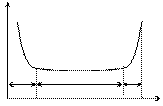 
l=Сonst
1 2 3
0 t1 t2 t
Рис. 3.3
На рис. 3.3 представлена типичная зависимость l(t) ,
где
зона 1 - период приработки элемента ЭС,
зона 2 - период нормальной эксплуатации элемента (l=const);
зона 3 - период износа элемента ЭС.
Если l=const, то имеем - экспоненциальное распределение (наиболее часто используемое в энергетике для периода нормальной работы элементов ЭС).
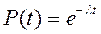; (3.30)
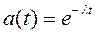; (3.31)
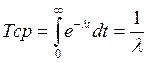. (3.32)
Таким образом, выражения (3.31) и (3.32) справедливы для периода нормальной работы элементов.
Для электрических сетей и ЛЭП формулы (11),(12) справедливы после 2-3 лет, эксплуатации, но учитывая, что срок службы ЛЭП 50-60 лет, то практически можно считать, что эти выражения применяются для оценки надежности ЛЭП и электрических сетей.
Зависимость P(t) - часто также называют надежностью работы элемента в заданном интервале времени. Так как:
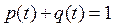, то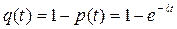 
(3.33)
Величину «q(t)» называют ненадежностью, это вероятность того, что за время «t» произойдет хотя бы один отказ.
Таким образом, для характеристики надежности надо знать величину l(t) – среднее число отказов в единицу времени.
5. Наработка на отказ То - среднее время безотказной работы невосстанавливаемых элементов до отказа или восстанавливаемого элемента между соседними отказами.
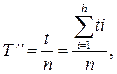(3.34)
где
n - число отказов за время испытания (эксплуатации) элемента ЭС;
t - общее время исправной работы элемента ЭС;
ti - время исправной работы элемента ЭС между (i-1) и i отказами.
6. Частота отказов (a) - плотность распределения времени безотказной работы или производная от вероятности безотказной работы
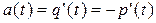(3.35)
Для определения величины a(t) используется следующая статистическая оценка:
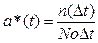, (3.36)
где
n(Dt) – общее количество элементов взятых для испытания или эксплуатируемых;
No – число отказавших элементов в интервале времени от (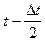 
) до ( 
);
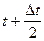Dt – интервал времени.
Покажем справедливость этой оценки. Число изделий, отказавших в течении «Dt»:
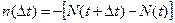, (3.37)
где
N(t) и N(t+Dt) – число изделий, безотказно проработавших в течении времени “t” и “(Dt + t)” соответственно.
При достаточно большом числе изделий, поставленных на испытание или эксплуатацию, имеем:
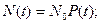(3.38)
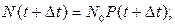(3.39)
Тогда
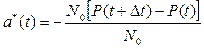. (3.40)
При Dt ® 0 получим:
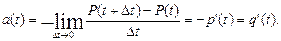(3.41)
Одновременно этот количественный показатель надёжности «а(t)» является дифференциальной функцией распределения вероятностей отказа (плотностью вероятности отказа) численно равной среднему числу отказов в единицу времени на один объект из начального количества объектов N0(t=0) или доле начального количества объектов N0(t=0), отказавших после произвольного, но фиксированного момента времени t в течении выбранного промежутка времени “Dt”.
Из теории вероятностей известно, что:
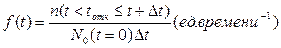(3.42)
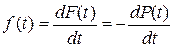и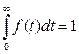 
(3.43)
Следовательно, график f(t) зависит от графика F(t). Зависимость же f(Dt) является пропорциональной, поскольку с ростом промежутка времени “Dt” возрастает и вероятность отказа в течении этого промежутка.
Сравнение формул плотности вероятности f(t) (3.42) и интенсивности отказов l(t) (3.44):
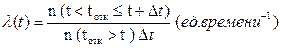(3.44)
показывает, что эти величины отличаются только общим количеством объектов в знаменателе, к которым относится количество элементов в числителе n (t < tотк £ t+ Dt), отказавших после произвольного, но фиксированного момента времени “t” в течение выбранного промежутка времени “Dt”
Частота отказов, вероятность безотказной работы и вероятность появления отказа связаны следующими зависимостями:
; 
;
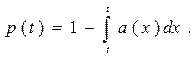
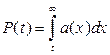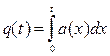(3.45)
так как p(t)=1-q(t) =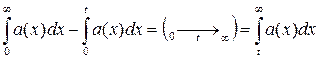 
Частота отказов элементов также связана с их интенсивностью отказов
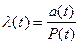(3.46)
Так как P(t) £ 1, то всегда l(t) ³ a(t).
Для высоконадежных систем при р(t)³0.99 можно принимать a(t) » l(t).
7. Дисперсия времени жизни элемента ЭС
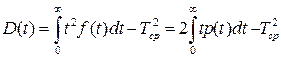(3.47)
Статистическая дисперсия:
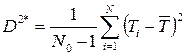, (3.48)
где
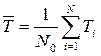
На практике в качестве оценки надёжности чаще используют среднее квадратическое отклонение ( s ) :
 |
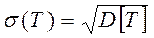(3.49)
где
Т – время жизни элемента ЭС.
Дата: 2019-02-02, просмотров: 252.
