Всякая система характеризуется безотказностью и ремонтопригодностью. В качестве основной характеристики безотказности системы служит функция надежности, которая представляет собой вероятность безотказной работы в течении некоторого времени «t».
Пусть система состоит из элементов функции надежности которых обозначим через р1(t), р2(t),...,рn(t). Т.к. эти элементы - независимые, то вероятность безотказной работы системы:
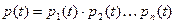(3.86)
Если функции надежности элементов имеют экспоненциальное распределение с постоянными интенсивностями отказов, то:
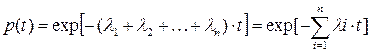(3.87)
Одной из важнейших характеристик безотказности системы (элемента) является среднее время ее жизни:
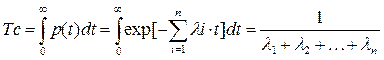(3.88)
Среднее время жизни системы или наработка ее на отказ равна:
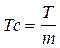, (3.89)
где
Т - суммарная наработка системы, полученная по результатам испытаний или эксплуатации;
m - суммарное число отказов, зафиксированное в процессе испытаний или эксплуатации.
В качестве основной характеристики ремонтопригодности служит среднее время восстановления системы:
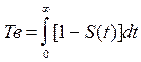(3.90)
где S(t) = Fв(t) – функция распределения времени восстановления.
Для случая пуассоновского потока восстановления имеем:
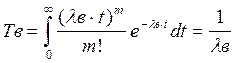(3.91)
где
lв = mв – интенсивность восстановления;
t - время восстановления.
Среднее время статистической модели восстановления системы по результатам испытания или эксплуатации:
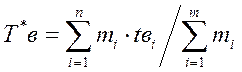(3.92)
где
mi - число отказов i-го элемента; tвi - время восстановления i-го отказа элемента.
Всякая система характеризуется комплексными показателями надежности, основными из которых являются коэффициенты готовности (КГ), технического использования (КТИ), оперативной готовности (КОГ).
Коэффициент «КГ» характеризует готовность элемента к применению по назначению в произвольный момент времени, кроме планируемых периодов обслуживания. Показатель - комплексный, т.к. зависит от безотказности и ремонтопригодности.
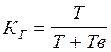(3.93)
где
Т - средняя наработка системы (элемента) на отказ;
Тв - среднее время восстановления отказа.
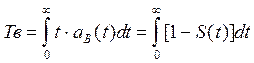(3.94)
где
S(t) - функция распределения времени восстановления;
аВ (t) - плотность распределения времени восстановления.
Статистическая оценка показателей надёжности (Тв*, Т*) составляет величину:
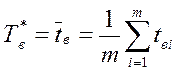(3.95)
где
tвi - время восстановления i-го отказа;
m - число отказов в рассматриваемом промежутке времени.
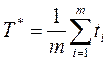(3.96)
где
ti - наработка системы до i-го отказа;
m - число отказов в интервале суммарной наработки.
Коэффициент технического использования, «КТИ», для независимых элементов ЭС, характеризует долю нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации. Этот период должен объединять все виды технического обслуживания и ремонтов.
Коэффициент «Кти» учитывает затраты времени на плановые и внеплановые ремонты:
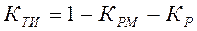; (3.97)
; 
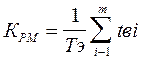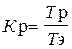. (3.98)
где
Тэ - период эксплуатации;
Тр - суммарное время на все виды обслуживания за период эксплуатации;
tвi - время восстановления i-го отказа;
m - число отказов в интервале суммарной наработки.
В формулах для КГ и КТИ среднее время жизни и среднее время восстановления элемента отражается выражениями (3.88-3.92).
Коэффициент оперативной готовности, «Ког», для независимых элементов ЭС, характеризует надежность системы, необходимость применения которой возникает в произвольный момент времени (кроме планируемых периодов, в течение которых применение системы по назначению не предусматривается), начиная с которого система будет работать безотказно в течение заданного интервала времени «t».
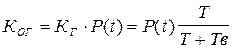. (3.99)
3.6 Показатели надёжности концентрированной ЭС и методы их определения
а) Вероятность снижения мощности ЭС
Однородная концентрированная ЭС - из одинаковых по всем параметрам генераторов , работающих на общую нагрузку. Показатели надёжности генераторов-qi , wi(вероятность отказа , частота попадания в неё).Число состояний ЭС (без плановых ремонтов)-"2".Если безразлично из-за отказа каких именно генераторов ЭС находится в том или ином состоянии , а важно на сколько снизилась мощность станций ЭС , то количество состояний ЭС изменяется до величины "n+1".При этом :нулевое состояние ЭС - все генераторы в работе, первое состояние ЭС - один генератор не работает , второе-два и т.д.
Попадание ЭС в одно из состояний соответствует схеме Бернулли и отвечает биноминальному распределению:
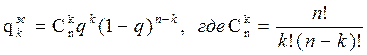(3.100)
где
q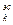 
- вероятность снижения мощности ЭС , при выходе из строя "k" генераторов;
n – общее количество работающих генераторов.
Интегральный закон распределения снижения мощности ЭС:
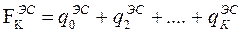(3.101)
б) Частота попадания Эс в Кое состояние:
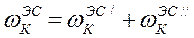(3.102)
где
wКЭС /-частота попадания ЭС в Кое состояние путём "сверху" при переходе в Кое состояние из (к-1) состояние
wКЭС //- частота попадания ЭС в Кое состояние путём "снизу" из (к+1) состояния ЭС.
Путь “сверху”:
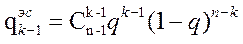- (3.103)
где
- вероятность ,что (к-1) генераторов простаивает
Средняя наработка К-го генератора в данном состоянии за время “t”.
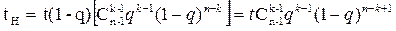. (3.104)
Количество отказов К-го генератора за время “t” в (к-1)-м состоянии ЭС:
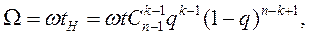(3.105)
где
w-частота отказов генератора.
Частота переходов системы в К-ое состояние из (к-1) из-за отказа К-го генератора
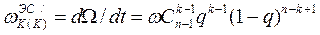(3.106)
Частота рассматриваемых событий , обусловленная отказом любого из «n» генераторов:
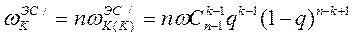(3.107)
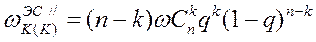(3.108)
Дата: 2019-02-02, просмотров: 228.
