Общий вид мультипликативной модели таков:
Y = T S ε.
Построение модели включает в себя следующие шаги:
1. выравнивание исходного ряда методом скользящей средней;
2. расчет значений сезонной компоненты S;
3. устранение сезонной компоненты из исходных уровней ряда (Y/S ) и получение выровненных данных (T ε);
4. аналитическое выравнивание уровней (T ε) и расчет значений T с использованием полученного уравнения тренда;
5. расчет полученных по модели значений (T S);
6. расчет ошибок.
Пример 4.7. Имеются поквартальные данные (усл. ед.) о выплате доходов компании акционерам в форме дивидендов за последние четыре года.
| Квартал | Год | |||
| 1 | 2 | 3 | 4 | |
| I | 40 | 60 | 50 | 30 |
| II | 50 | 80 | 70 | 50 |
| III | 60 | 100 | 80 | 60 |
| IV | 70 | 110 | 130 | 70 |
По графику ряда можно установить наличие приблизительно линейного тренда и сезонных колебаний (период равен 4) возрастающей амплитуды, поэтому используется мультипликативная модель. Определим ее компоненты.
Для исключения влияния сезонной компоненты произведем выравнивание исходного ряда методом скользящей средней за 4 квартала и процедуру центрирования. Результаты расчетов представлены в таблице.
| Номер квартала | Размер дивидендов, yt | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 1 | 40 | |||
| 2 | 60 | 45 | ||
| 3 | 50 | 47,5 | 46,25 | 1,081 |
| 4 | 30 | 52,5 | 50 | 0,600 |
| 5 | 50 | 57,5 | 55 | 0,909 |
| 6 | 80 | 62,5 | 60 | 1,333 |
| 7 | 70 | 65 | 63,75 | 1,098 |
| 8 | 50 | 70 | 67,5 | 0,741 |
| 9 | 60 | 72,5 | 71,25 | 0,842 |
| 10 | 100 | 75 | 73,75 | 1,356 |
| 11 | 80 | 77,5 | 76,25 | 1,049 |
| 12 | 60 | 80 | 78,75 | 0,762 |
| 13 | 70 | 92,5 | 86,25 | 0,811 |
| 14 | 110 | 95 | 93,75 | 1,173 |
| 15 | 130 | |||
| 16 | 70 |
Оценки сезонной вариации для мультипликативной модели определяются как частное от деления фактических уровней ряда yt на центрированные скользящие средние.
Расчет сезонной компоненты произведем в следующей расчетной таблице, в которой оценки сезонной вариации записываются под соответствующим номером квартала в году.
| Показатели | Год | Номер квартала в году |
| |||
| I | II | III | IY | |||
|
| 1 | 1,081 | 0,600 | |||
| 2 | 0,909 | 1,333 | 1,098 | 0,741` | ||
| 3 | 0,842 | 1,356 | 1,049 | 0,762 | ||
| 4 | 0,811 | 1,173 | ||||
| Итого | 2,562 | 3,862 | 3,228 | 2,103 | Сумма | |
| Среднее | 0,854 | 1,287 | 1,076 | 0,701 | 3,918 | |
| Скорректированное Si | 0,872 | 1,314 | 1,099 | 0,715 | 4 | |
В строке Среднее рассчитаны средние сезонной вариации по годам за каждый квартал и их Сумма = 3,918.
В мультипликативной модели предполагается, что сумма всех сезонных компонент по всем кварталам должна быть равна 4 – числу сезонов в году (условие взаимопогашаемости сезонных воздействий).
В строке Скорректированное рассчитаны значения сезонных компонент Si как произведение соответствующей средней сезонной вариации на корректирующий коэффициент 4 / 3,918 = 1,021, при этом S Si = 4.
Расчет трендовой компоненты и ошибок произведем в следующей таблице.
| t | Y | S | Y/S=T × e | T | e=Y/(TS) | e=Y – (TS) |
| 1 | 40 | 0,872 | 45,871 | 38,97 | 1,18 | 6,02 |
| 2 | 60 | 1,314 | 45,662 | 43,046 | 1,06 | 3,44 |
| 3 | 50 | 1,099 | 45,496 | 47,122 | 0,96 | –1,79 |
| 4 | 30 | 0,715 | 41,958 | 51,197 | 0,82 | –6,60 |
| 5 | 50 | 0,872 | 57,335 | 55,273 | 1,04 | 1,80 |
| 6 | 80 | 1,314 | 60,883 | 59,349 | 1,02 | 2,01 |
| 7 | 70 | 1,099 | 63,694 | 63,425 | 1,00 | 0,29 |
| 8 | 50 | 0,715 | 69,930 | 67,501 | 1,03 | 1,73 |
| 9 | 60 | 0,872 | 68,807 | 71,577 | 0,96 | –2,41 |
| 10 | 100 | 1,314 | 76,103 | 75,652 | 1,00 | 0,59 |
| 11 | 80 | 1,099 | 72,793 | 79,728 | 0,91 | –7,62 |
| 12 | 60 | 0,715 | 83,916 | 83,804 | 1,00 | 0,08 |
| 13 | 70 | 0,872 | 80,275 | 87,880 | 0,91 | –6,63 |
| 14 | 110 | 1,314 | 83,713 | 91,956 | 0,91 | –10,83 |
| 15 | 130 | 1,099 | 118,289 | 96,032 | 1,23 | 24,46 |
| 16 | 70 | 0,715 | 97,902 | 100.108 | 0,98 | –1,58 |
Разделив каждый уровень исходного ряда на соответствующие значения сезонной компоненты (столбец Y/S= T × e), исключим влияние сезонной компоненты и в результате получим только тенденцию и случайную компоненту.
Производя аналитическое выравнивание ряда (T × e) с помощью линейного тренда, получим следующее уравнение линии тренда: T = 34,89 + 4,087× t.
Уровни ряда T для каждого t = 1, 2, …, 16 приведены в таблице.
Графики исходного ряда и его тренда приведены на рис. 14.
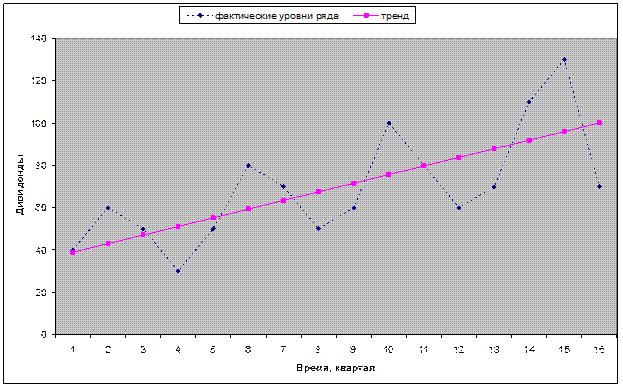
Рис. 14
Расчет ошибки в мультипликативной модели производится по формуле
e = Y/(T×S).
Чтобы сравнивать мультипликативную модель с другими моделями временного ряда, ошибки в мультипликативной модели определяются как
e = Y – (T×S).
В этом случае для оценки качества построенной модели можно по аналогии с аддитивной моделью использовать выражение
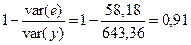 ,
,
т.е. мультипликативная модель объясняет 91,0 % общей вариации уровней исходного временного ряда.
Дата: 2019-02-02, просмотров: 395.