Анализ вариации зависимой переменной
Пусть в уравнении регрессии содержится k объясняющих переменных. Допустим, что можно разложить дисперсию зависимой переменной на объясненную и необъясненную составляющие:
.
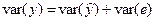Используя определение выборочной дисперсии, это уравнение можно представить в виде:
.
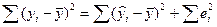Обозначим:
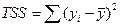– общий разброс зависимой переменной;
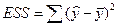– разброс, объясненный регрессией;
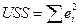– разброс, не объясненный регрессией.
Тогда
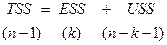
(в скобках указано число степеней свободы, соответствующее каждому члену уравнения).
Замечание. Любая сумма квадратов связана с числом степеней свободы, т.е. с числом независимого варьирования переменной. Существует равенство между числом степеней свободы для этого уравнения. Отнесение каждой суммы квадратов этого уравнения на одну степень свободы приводит их к сравнимому виду.
Коэффициент детерминации есть доля объясненной части разброса зависимой переменной, т.е.
.
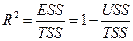Величина R2 является мерой объясняющего качества уравнения регрессии по сравнению с горизонтальной линией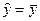 
.
Поскольку коэффициент R2 измеряет долю дисперсии, совместно объясненной независимыми переменными, то, казалось бы, можно определить отдельный вклад каждой независимой переменной и таким образом получить меру ее относительной важности. Однако такое разложение невозможно, если независимые переменные коррелированы, поскольку в этом случае их объясняющие способности будут перекрываться.
На рис. 12 показана иллюстрация коэффициента детерминации при использовании одной и двух объясняющих переменных.
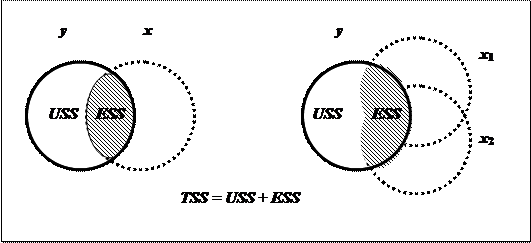
Рис. 12
С увеличением объясненной части разброса ESS коэффициент R2 приближается к единице. Кроме того, с добавлением еще одной переменной R2 обычно увеличивается.
Для компенсации такого увеличения R2 вводится скорректированный коэффициент детерминации с поправкой на число степеней свободы:
.
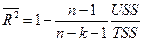Если увеличение доли объясненной регрессии при добавлении новой переменной мало, то скорректированный коэффициент детерминации может уменьшиться, следовательно, добавлять переменную нецелесообразно.
Кроме того, если объясняющие переменные x1 и x2 сильно коррелируют между собой, то они объясняют одну и ту же часть разброса переменной y, и в этом случае трудно оценить вклад каждой из переменных в объяснение поведения y.
Мультиколлинеарность
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. При наличии мультиколлинеарности МНК-оценки формально существуют, но обладают рядом недостатков:
1) небольшое изменение исходных данных приводит к существенному изменению оценок регрессии;
2) оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокое значение R2).
Если при оценке уравнения регрессии несколько факторов оказались незначимы, то нужно выяснить, нет ли среди них сильно коррелированных между собой.
При наличии корреляции один из пары связанных между собой факторов исключается либо в качестве объясняющего фактора берется какая-то их функция. Если статистически незначим лишь один фактор, то он должен быть исключен либо заменен другим показателем.
Для отбора факторов в модель регрессии и оценки их мультиколлинеарности можно использовать матрицу парных коэффициентов корреляции (расчет корреляционной матрицы можно выполнить в MS Excel).
В модель регрессии включаются те факторы, которые сильнее связаны с зависимой переменной, но слабо связанные с другими факторами.
Упражнение 4.2. Пусть по данным бюджетного обследования семи случайно выбранных семей изучалась зависимость накопления y от дохода x1, расходов на питание x2 и стоимости имущества x3. Исходные данные (усл. ед.):
| x1 | 40 | 55 | 45 | 30 | 30 | 60 | 50 |
| x2 | 10 | 15 | 12 | 8 | 10 | 20 | 15 |
| x3 | 60 | 40 | 40 | 15 | 90 | 30 | 30 |
| y | 2 | 7 | 5 | 4 | 2 | 7 | 6 |
Используя инструменты MS Excel, получите матрицу парных коэффициентов корреляции:
| y | x1 | х2 | x3 | |
| y | 1 | |||
| х1 | 0,85 | 1 | ||
| х2 | 0,81 | 0,93 | 1 | |
| х3 | –0,65 | –0,38 | –0,28 | 1 |
Проанализируйте целесообразность включения в модель каждого фактора.
Замещающие переменные
Предположим, что истинной моделью является
y = a + b1x1 + b2x2 + … + b k xk + e,
и допустим, что не имеется данных по существенной переменной x1.
Если не включить в модель эту переменную, то регрессия может пострадать от смещения оценок и статистическая проверка будет некорректной.
Если вместо отсутствующей переменной x1 использовать её заменитель z, линейно связанный с x1 и построить регрессию
,
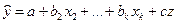то оценки b2, …, bk, их стандартные ошибки и коэффициент R2 будут такими же, как с использованием x1. Единственным недостатком является то, что отсутствует оценка коэффициента при самой величине x1, а величина a не является оценкой a.
В качестве замещающей переменной, например, для показателя технического прогресса может использоваться время.
Фиктивные переменные
При исследовании влияния качественных признаков в модель можно вводить фиктивные переменные, принимающие, как правило, два значения: единица, если данный признак присутствует в наблюдении, и ноль при его отсутствии.
Если включаемый в рассмотрение качественный признак имеет не два, а несколько значений, то используют несколько фиктивных переменных, число которых должно быть на единицу меньше числа значений признака.
При назначении фиктивных переменных исследуемая совокупность по числу значений качественного признака разбивается на группы. Одну из групп выбирают как эталонную (группа 0) и определяют фиктивные переменные для остальных.
Например, если качественный признак имеет три значения, то две фиктивные переменные определяются следующим образом:
- группа 0: z1 = z2 = 0,
- группа 1: z1 = 1, z2 = 0,
- группа 2: z1 = 0, z2 = 1,
или
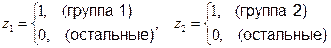
Введение в регрессию фиктивных переменных существенно улучшает качество ее оценивания.
Пример 4.3. Имеются данные о весе y новорожденного в граммах и количестве x сигарет, выкуриваемых в день будущей матерью во время беременности в случаях, когда рожала женщина до этого или нет.
| № | Первенец? | y | x | D | № | Первенец? | y | x | D |
| 1 | Нет | 3450 | 8 | 1 | 11 | Нет | 3200 | 31 | 1 |
| 2 | Нет | 3300 | 21 | 1 | 12 | Нет | 3400 | 13 | 1 |
| 3 | Нет | 3400 | 18 | 1 | 13 | Да | 3450 | 5 | 0 |
| 4 | Нет | 3300 | 24 | 1 | 14 | Да | 3400 | 10 | 0 |
| 5 | Нет | 3450 | 6 | 1 | 15 | Да | 3200 | 19 | 0 |
| 6 | Нет | 3450 | 16 | 1 | 16 | Да | 3350 | 12 | 0 |
| 7 | Нет | 3100 | 19 | 1 | 17 | Да | 3000 | 20 | 0 |
| 8 | Нет | 3500 | 7 | 1 | 18 | Да | 3300 | 8 | 0 |
| 9 | Нет | 3400 | 20 | 1 | 19 | Да | 3300 | 16 | 0 |
| 10 | Нет | 3500 | 10 | 1 | 20 | Да | 3400 | 9 | 0 |
Оценив регрессию между y и x, получим выражение:
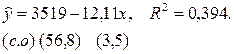
Это означает, что ребенок, рожденной некурящей матерью, будет иметь при рождении средний вес около 3500 г, и что уменьшение веса новорожденного по причине курения составляет около 12 г на каждую сигарету, выкуриваемую в день будущей матерью.
Для учета качественного фактора (родился ли ребенок первым или не первым) введем в модель фиктивную переменную:
.
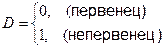Оценив регрессию между y и x, D, получим выражение:
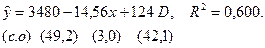
Коэффициент 124 при фиктивной переменной D статистически значим.
Это выражение можно переписать в виде двух уравнений:
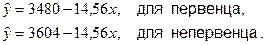
Параметр сдвига (эффект от фактора «первенец-непервенец») составляет 3604 – 3480 = 124 грамма.
Как видим, добавление в регрессию фиктивной переменной существенно улучшило качество оценки.
Лаговые переменные
При использовании данных временного ряда на текущие значения зависимой переменной могут влиять не только текущие значения объясняющих переменных, но также их значения с некоторым запаздыванием.
В общем, если какая-то переменная появляется в модели с запаздыванием на t периодов, она записывается с нижним индексом (t – t), например,
yt = b0 + b1xt + b2xt– t + e t.
Сдвиг t, характеризующий запаздывание в воздействии фактора на результат называется лагом. Переменная, влияние которой характеризуется некоторым запаздыванием, называется лаговой.
Понятие о временных рядах
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов времени.
Каждый уровень y(t) временного ряда формируется под совместным влиянием длительных, кратковременных и случайных факторов
Длительные постоянно действующие факторы оказывают на изучаемое явление определяющее влияние и формируют основную тенденцию ряда – тренд T(t). Кратковременные, периодические факторы формируют сезонные колебания ряда S(t). Случайные факторы отражаются случайными изменениями уровней ряда e(t).
Модель, в которой временной ряд представлен как сумма перечисленных компонентов, т.е.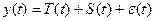 
, называется аддитивной.
Модель, в которой временной ряд представлен как произведение перечисленных компонентов, т.е.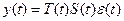 
, называется мультипликативной.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний.
Если амплитуда сезонных колебаний приближенно постоянная, то используют аддитивную модель.
Если амплитуда возрастает или уменьшается, то используют мультипликативную модель.
Основная задача эконометрического исследования временного ряда – выявление каждой из перечисленных компонент ряда.
Анализ аддитивной модели
Общий вид аддитивной модели таков:
Y = T + S + ε.
Построение модели включает в себя следующие шаги:
1. выравнивание исходного ряда методом скользящей средней;
2. расчет значений сезонной компоненты S;
3. устранение сезонной компоненты из исходных уровней ряда (Y – S) и получение выровненных данных (T + ε);
4. аналитическое выравнивание уровней (T + ε) и расчет значений T с использованием полученного уравнения тренда;
5. расчет полученных по модели значений (T + S);
6. расчет абсолютных ошибок.
Пример 4.6. Имеются данные (усл. ед.) об объеме потребления электроэнергии y в некотором районе за четыре года (поквартально).
| Квартал | Год | |||
| 1 | 2 | 3 | 4 | |
| I | 6,0 | 7,2 | 8,0 | 9,0 |
| II | 4,4 | 4,8 | 5,6 | 6,6 |
| III | 5,0 | 6,0 | 6,4 | 7,0 |
| IY | 9,0 | 10,0 | 11,0 | 10,8 |
В качестве зависимой переменной при анализе временного ряда выступают фактические уровни ряда yt, а в качестве независимой переменной – время (номер квартала) t = 1, 2, …, 16.
По графику ряда можно приблизительно установить наличие линейного тренда и сезонных колебаний (период равен 4) одинаковой амплитуды, поэтому используется аддитивная модель. Определим ее компоненты.
Для исключения влияния сезонной компоненты произведем выравнивание исходного ряда методом скользящей средней за 4 квартала и процедуру центрирования. Результаты расчетов представлены в таблице.
| Номер квартала | Потребление электроэнергии, yt | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 1 | 6,0 | |||
| 2 | 4,4 | 6,10 | ||
| 3 | 5,0 | 6,40 | 6,250 | -1,250 |
| 4 | 9,0 | 6,50 | 6,450 | 2,550 |
| 5 | 7,2 | 6,75 | 6,625 | 0,575 |
| 6 | 4,8 | 7,00 | 6,875 | -2,075 |
| 7 | 6,0 | 7,20 | 7,100 | -1,100 |
| 8 | 10,0 | 7,40 | 7,300 | 2,700 |
| 9 | 8,0 | 7,50 | 7,450 | 0,550 |
| 10 | 5,6 | 7,75 | 7,625 | -2,025 |
| 11 | 6,4 | 8,00 | 7,875 | -1,475 |
| 12 | 11,0 | 8,25 | 8,125 | 2,875 |
| 13 | 9,0 | 8,40 | 8,325 | 0,675 |
| 14 | 6,6 | 8,35 | 8,375 | -1,775 |
| 15 | 7,0 | |||
| 16 | 10,8 |
На рис. 13 представлены графики фактических уровней ряда и центрированной скользящей средней.
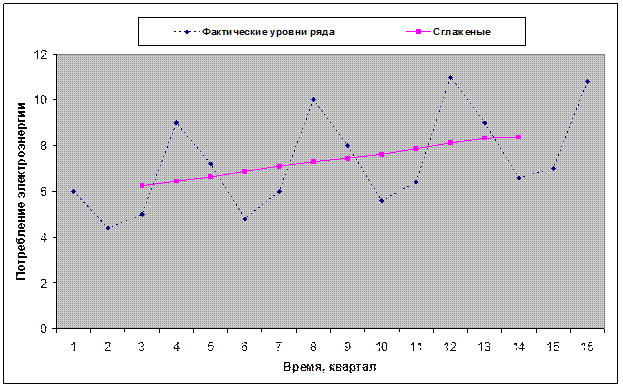
Рис. 13
Оценки сезонной вариации определяются как разность между фактическими уровнями ряда yt и центрированными скользящими средними.
Расчет сезонной компоненты произведем в следующей расчетной таблице, в которой оценки сезонной вариации записываются под соответствующим номером квартала в году.
| Показатели | Год | Номер квартала в году |
| |||
| I | II | III | IY | |||
|
| 1 | -1,250 | 2,550 | |||
| 2 | 0,575 | -2,075 | -1,100 | 2,700 | ||
| 3 | 0,550 | -2.025 | -1,475 | 2,875 | ||
| 4 | 0,675 | -1,775 | ||||
| Итого | 1,800 | -5,875 | -3,825 | 8,125 | Сумма | |
| Среднее | 0,600 | -1,958 | -1,275 | 2,708 | 0,075 | |
| Скорректированное Si | 0,581 | -1,977 | -1,294 | 2,690 | 0 | |
В строке Среднее рассчитаны средние сезонной вариации по годам за каждый квартал и их сумма равна 0,075.
В аддитивной модели предполагается, что сумма всех сезонных компонент по всем кварталам должна быть равна нулю (условие взаимопогашаемости сезонных воздействий).
В строке Скорректированное рассчитаны значения сезонных компонент Si как разность между средней сезонной вариацией и корректирующим коэффициентом 0,075/4, при этом S Si = 0.
Расчет трендовой компоненты и ошибок произведем в следующей таблице
| t | Y | S | Y – S = T + e | T | Ошибка e |
| 1 | 6,0 | 0,581 | 5,419 | 5,893 | -0,474 |
| 2 | 4,4 | -1,977 | 6,337 | 6,088 | 0,256 |
| 3 | 5,0 | -1,294 | 6,294 | 6,268 | 0,025 |
| 4 | 9,0 | 2,690 | 6,310 | 6,455 | -0,145 |
| 5 | 7,2 | 0,581 | 6,619 | 6,642 | -0,023 |
| 6 | 4,8 | -1,977 | 6,777 | 6,829 | -0,052 |
| 7 | 6,0 | -1,294 | 7,294 | 7,016 | 0,277 |
| 8 | 10,0 | 2,690 | 7,310 | 7,204 | 0,106 |
| 9 | 8,0 | 0,581 | 7,419 | 7,391 | 0.027 |
| 10 | 5,6 | -1,977 | 7,577 | 7,578 | -0,001 |
| 11 | 6,4 | -1,294 | 7,694 | 7,765 | -0,071 |
| 12 | 11,0 | 2,690 | 8,310 | 7,952 | 0,357 |
| 13 | 9,0 | 0,581 | 8,419 | 8,139 | 0,279 |
| 14 | 6,6 | -1,977 | 8,577 | 8,326 | 0,250 |
| 15 | 7,0 | -1,294 | 8,294 | 8,514 | -0,220 |
| 16 | 10,8 | 2,690 | 8,110 | 8,701 | -0,591 |
В столбце Y – S = T + e исключается влияние сезонной компоненты; вычитая ее значение из каждого уровня исходного ряда, в результате получим только тенденцию и случайную компоненту.
Производя аналитическое выравнивание ряда (T + e) с помощью линейного тренда, получим следующее уравнение линии тренда: T = 5,706 + 0,187×t.
Уровни ряда T для каждого t = 1, 2, …, 16 приведены в таблице.
Расчет ошибки в аддитивной модели производится по формуле e = Y – (T + S).
Дисперсии фактического ряда и ошибки, рассчитанные в Excel с помощью функции ДИСПР, составляют: var(y) = 4,196, var(e) = 0,0684.
Для оценки качества построенной модели по аналогии с моделью регрессии можно использовать выражение
,
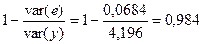т.е. аддитивная модель объясняет 98, 4% общей вариации уровней временного ряда потребления электроэнергии.
Глава 4. Модель множественной регрессии
Обобщением линейной регрессионной модели с одной объясняющей переменной является линейная регрессионная модель с k объясняющими переменными (модель множественной регрессии):
y = b0 + b1 x1 +…+ b k xk + e,
где b 0 , b 1 ,…, b k – параметры модели, а e случайный член.
Случайный член e удовлетворяет тем же предпосылкам, что и в модели с парной регрессией, называемым условиями Гаусса-Маркова:
1) математическое ожидание случайного члена в любом наблюдении должно быть равно нулю, т.е.
M(e i) = 0, (i = 1, n);
2) дисперсия случайного члена должна быть постоянной для всех наблюдений, т.е.
D(e i) = M(e i2) = s2, (i = 1, n);
3) случайные члены должны быть статистически независимы (некоррелированы) между собой, т.е.
M(e i e j) = 0, (i ¹ j);
4) случайные члены в любом наблюдении должны быть статистически независимы от объясняющих переменных.
При выполнении условий Гаусса-Маркова модель называется классической нормальной линейной регрессионной моделью.
Предполагается, что объясняющие переменные некоррелированны друг с другом.
На основе n наблюдений оценивается выборочное уравнение регрессии:
,
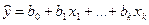где b0, b1, … ,bk оценки параметров b0, b1, …, bk.
Для оценки параметров регрессии используется метод наименьших квадратов. В соответствии с МНК, минимизируется сумма квадратов остатков:
.
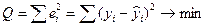Необходимым условием ее минимума является равенство нулю всех ее частных производных по b0, b1, …, bk.
В результате приходим к системе из (k + 1) линейных уравнений с (k + 1) неизвестными, называемой системой нормальных уравнений. Ее решение в явном виде обычно записывается в матричной форме, иначе оно становится слишком громоздким.
Оценки параметров модели и их теоретические дисперсии в матричной форме определяются выражениями:
, 
,
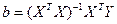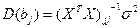где b – вектор с компонентами b0, b1, …, bk; X – матрица значений объясняющих переменных; Y – вектор значений зависимой переменной; s2 - дисперсия случайного члена.
Несмещенной оценкой s2 является величина S2 (остаточная дисперсия):
.
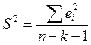Величина S называется стандартной ошибкой регрессии.
Заменяя в теоретических дисперсиях неизвестную дисперсию s2 на её оценку S2 и извлекая квадратный корень, получим стандартные ошибки коэффициентов регрессии:
.
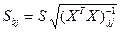Если предпосылки относительно случайного члена e выполняются, оценки параметров множественной регрессии являются несмещенными, состоятельными и эффективными.
При использовании компьютерных программ коэффициенты регрессии b0, b1, …, bk и их стандартные отклонения вычисляются одновременно.
Пример 4.1. По данным бюджетного обследования семи случайно выбранных семей изучалось зависимость накопления y от дохода x1 и имущества x2.
Исходные данные (усл. ед):
| X1 | 40 | 55 | 45 | 30 | 30 | 60 | 50 |
| X2 | 60 | 40 | 40 | 15 | 90 | 30 | 30 |
| Y | 2 | 7 | 5 | 4 | 2 | 7 | 6 |
Для того, чтобы использовать инструмент Регрессия из Пакета анализа, необходимо транспонировать исходные данные. Получим оцененное уравнение регрессии:
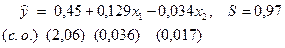
(в скобках указаны стандартные ошибки).
Из этого уравнения можно сделать следующие выводы.
1. Прогнозируемое накопление семьи, имеющей доход 40 усл. ед и имущество стоимостью 25 усл. ед составляет:
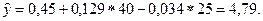
2. Если доход семьи возрастет на 10 усл. ед, а стоимость имущества не изменится, то накопление возрастет на величину:
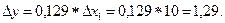
3. Если доход семьи возрастет на 5 усл. ед, а стоимость имущества увеличится на 15 усл. ед, то накопление возрастет на величину:
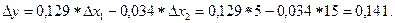
Замечание. Для прогноза значения переменной y при заданных значениях x объясняющих переменных можно воспользоваться статистической функцией Excel: ТЕНДЕНЦИЯ.
Дата: 2019-02-02, просмотров: 333.
