Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Задача выявления основной тенденции развития в статистике называется выравниванием временного ряда.
Методами выявления тренда являются:
- метод укрупнения интервалов;
- метод скользящей средней;
- аналитическое выравнивание.
Метод укрупнения интервалов. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда. При суммировании уровней по укрупненным интервалам колебания в уровнях, обусловленные случайными причинами, взаимнопогашаются и более четко обнаруживается общая тенденция.
Метод скользящей средней. Метод сглаживание скользящей средней заключается в том, что рассматривается средний уровень из определенного числа первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, продвигаясь на один срок.
Пример 4.5. Произведем расчет скользящей средней по данным об урожайности зерновых культур (ц/га) за 10 лет.
Исходные данные и расчетные показатели представлены в таблице.
| Год | Фактический уровень | Скользящая средняя | Центрированная скользящая средняя | |
| Трехлетняя | Четырехлетняя | |||
| 1986 | 15 | |||
| 1987 | 13 | 14,33 | 14,75 | |
| 1988 | 15 | 14,67 | 15,50 | 15,125 |
| 1989 | 16 | 16,33 | 16,50 | 16 |
| 1990 | 18 | 17,00 | 16,75 | 16,625 |
| 1991 | 17 | 17,00 | 17,50 | 17,125 |
| 1992 | 16 | 17,33 | 17,25 | 17,375 |
| 1993 | 19 | 17,33 | 18 | 17,625 |
| 1994 | 17 | 18,67 | ||
| 1995 | 20 | |||
Период скольжения может быть четным и нечетным. Для нечетного периода (трехлетняя) первое значение скользящей средней есть (15 + 13 + 15)/3 = 14,33, второе – (13 + 15 + 16)/3 = 14,67 и т.д, причем полученные результаты скользящей средней отнесены к середине периода скольжения.
Для четного периода (четырехлетняя) первое значение скользящей средней есть (15 + 13 + 15 + 16)/4 = 14,75, второе – (13 + 15 + 16 + 18)/4 = 15,50 и т.д., но рассчитанные усредненные значения нельзя сопоставить каким-либо определенным значениям t, поэтому применяют процедуру центрирования (вычисляют среднее значение из двух последовательных скользящих средних). Первое значение центрированной скользящей средней есть (14,75 + 15,50)/2 = 15,125, второе – (15,50 + 16,50)/2 = 16 и т.д., причем, первая центрированная средняя будет отнесена к третьему году.
Замечание. Используя пакет анализа Excel (Скользящее среднее), можно также получить результаты сглаживания.
Метод аналитического выравнивания. В этом методе фактические уровни ряда заменяются плавно изменяющимися уровнями, полученные из уравнения регрессии yt = f(t) + e. При аналитическом выравнивании используются различные виды трендовых моделей.
Упражнение 4.3. Имеются данные о розничном товарообороте региона (усл. ед.) за 10 лет:
| № года | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Товарооборот | 11 | 13 | 22 | 18,5 | 20 | 19 | 25 | 23 | 24,5 | 35 |
Построить следующие трендовые модели товарооборота и выбрать из них наиболее подходящий:
| Вид уравнения | Уравнение | R2 |
| Линейное | Y = 1,94× t + 10,43 | 0,767 |
| Полином 2-го порядка | Y = 0,074×t2 + 1,127× t + 12,06 | 0,774 |
| Полином 3-го порядка | Y = 0,121×t3 – 1,921× t2 + 10,33×t +1,68 | 0,886 |
| Логарифмическое | Y = 7,70×ln(t) + 9,46 | 0,709 |
| Степенное | Y = 10,88×t0,407 | 0,815 |
| Экспоненциальное | Y = 11,84×e0,096×t | 0.781 |
Замечание. Для нахождения наиболее адекватного уравнения тренда в Excel используется инструмент «Подбор линии тренда» из Мастера диаграмм.
Анализ аддитивной модели
Общий вид аддитивной модели таков:
Y = T + S + ε.
Построение модели включает в себя следующие шаги:
1. выравнивание исходного ряда методом скользящей средней;
2. расчет значений сезонной компоненты S;
3. устранение сезонной компоненты из исходных уровней ряда (Y – S) и получение выровненных данных (T + ε);
4. аналитическое выравнивание уровней (T + ε) и расчет значений T с использованием полученного уравнения тренда;
5. расчет полученных по модели значений (T + S);
6. расчет абсолютных ошибок.
Пример 4.6. Имеются данные (усл. ед.) об объеме потребления электроэнергии y в некотором районе за четыре года (поквартально).
| Квартал | Год | |||
| 1 | 2 | 3 | 4 | |
| I | 6,0 | 7,2 | 8,0 | 9,0 |
| II | 4,4 | 4,8 | 5,6 | 6,6 |
| III | 5,0 | 6,0 | 6,4 | 7,0 |
| IY | 9,0 | 10,0 | 11,0 | 10,8 |
В качестве зависимой переменной при анализе временного ряда выступают фактические уровни ряда yt, а в качестве независимой переменной – время (номер квартала) t = 1, 2, …, 16.
По графику ряда можно приблизительно установить наличие линейного тренда и сезонных колебаний (период равен 4) одинаковой амплитуды, поэтому используется аддитивная модель. Определим ее компоненты.
Для исключения влияния сезонной компоненты произведем выравнивание исходного ряда методом скользящей средней за 4 квартала и процедуру центрирования. Результаты расчетов представлены в таблице.
| Номер квартала | Потребление электроэнергии, yt | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 1 | 6,0 | |||
| 2 | 4,4 | 6,10 | ||
| 3 | 5,0 | 6,40 | 6,250 | -1,250 |
| 4 | 9,0 | 6,50 | 6,450 | 2,550 |
| 5 | 7,2 | 6,75 | 6,625 | 0,575 |
| 6 | 4,8 | 7,00 | 6,875 | -2,075 |
| 7 | 6,0 | 7,20 | 7,100 | -1,100 |
| 8 | 10,0 | 7,40 | 7,300 | 2,700 |
| 9 | 8,0 | 7,50 | 7,450 | 0,550 |
| 10 | 5,6 | 7,75 | 7,625 | -2,025 |
| 11 | 6,4 | 8,00 | 7,875 | -1,475 |
| 12 | 11,0 | 8,25 | 8,125 | 2,875 |
| 13 | 9,0 | 8,40 | 8,325 | 0,675 |
| 14 | 6,6 | 8,35 | 8,375 | -1,775 |
| 15 | 7,0 | |||
| 16 | 10,8 |
На рис. 13 представлены графики фактических уровней ряда и центрированной скользящей средней.
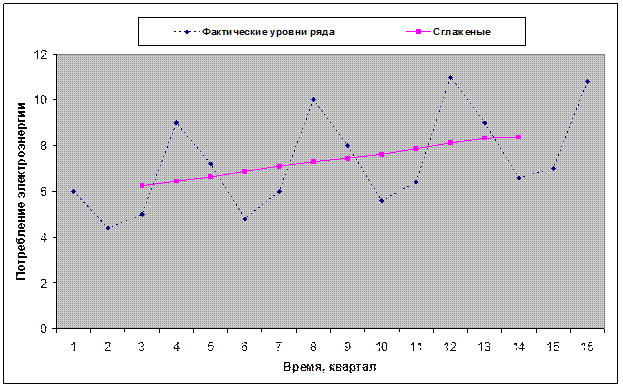
Рис. 13
Оценки сезонной вариации определяются как разность между фактическими уровнями ряда yt и центрированными скользящими средними.
Расчет сезонной компоненты произведем в следующей расчетной таблице, в которой оценки сезонной вариации записываются под соответствующим номером квартала в году.
| Показатели | Год | Номер квартала в году |
| |||
| I | II | III | IY | |||
|
| 1 | -1,250 | 2,550 | |||
| 2 | 0,575 | -2,075 | -1,100 | 2,700 | ||
| 3 | 0,550 | -2.025 | -1,475 | 2,875 | ||
| 4 | 0,675 | -1,775 | ||||
| Итого | 1,800 | -5,875 | -3,825 | 8,125 | Сумма | |
| Среднее | 0,600 | -1,958 | -1,275 | 2,708 | 0,075 | |
| Скорректированное Si | 0,581 | -1,977 | -1,294 | 2,690 | 0 | |
В строке Среднее рассчитаны средние сезонной вариации по годам за каждый квартал и их сумма равна 0,075.
В аддитивной модели предполагается, что сумма всех сезонных компонент по всем кварталам должна быть равна нулю (условие взаимопогашаемости сезонных воздействий).
В строке Скорректированное рассчитаны значения сезонных компонент Si как разность между средней сезонной вариацией и корректирующим коэффициентом 0,075/4, при этом S Si = 0.
Расчет трендовой компоненты и ошибок произведем в следующей таблице
| t | Y | S | Y – S = T + e | T | Ошибка e |
| 1 | 6,0 | 0,581 | 5,419 | 5,893 | -0,474 |
| 2 | 4,4 | -1,977 | 6,337 | 6,088 | 0,256 |
| 3 | 5,0 | -1,294 | 6,294 | 6,268 | 0,025 |
| 4 | 9,0 | 2,690 | 6,310 | 6,455 | -0,145 |
| 5 | 7,2 | 0,581 | 6,619 | 6,642 | -0,023 |
| 6 | 4,8 | -1,977 | 6,777 | 6,829 | -0,052 |
| 7 | 6,0 | -1,294 | 7,294 | 7,016 | 0,277 |
| 8 | 10,0 | 2,690 | 7,310 | 7,204 | 0,106 |
| 9 | 8,0 | 0,581 | 7,419 | 7,391 | 0.027 |
| 10 | 5,6 | -1,977 | 7,577 | 7,578 | -0,001 |
| 11 | 6,4 | -1,294 | 7,694 | 7,765 | -0,071 |
| 12 | 11,0 | 2,690 | 8,310 | 7,952 | 0,357 |
| 13 | 9,0 | 0,581 | 8,419 | 8,139 | 0,279 |
| 14 | 6,6 | -1,977 | 8,577 | 8,326 | 0,250 |
| 15 | 7,0 | -1,294 | 8,294 | 8,514 | -0,220 |
| 16 | 10,8 | 2,690 | 8,110 | 8,701 | -0,591 |
В столбце Y – S = T + e исключается влияние сезонной компоненты; вычитая ее значение из каждого уровня исходного ряда, в результате получим только тенденцию и случайную компоненту.
Производя аналитическое выравнивание ряда (T + e) с помощью линейного тренда, получим следующее уравнение линии тренда: T = 5,706 + 0,187×t.
Уровни ряда T для каждого t = 1, 2, …, 16 приведены в таблице.
Расчет ошибки в аддитивной модели производится по формуле e = Y – (T + S).
Дисперсии фактического ряда и ошибки, рассчитанные в Excel с помощью функции ДИСПР, составляют: var(y) = 4,196, var(e) = 0,0684.
Для оценки качества построенной модели по аналогии с моделью регрессии можно использовать выражение
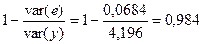 ,
,
т.е. аддитивная модель объясняет 98, 4% общей вариации уровней временного ряда потребления электроэнергии.
Дата: 2019-02-02, просмотров: 372.