Построение экономической модели включает выбор объясняющих переменных. Свойства оценок коэффициентов регрессии в значительной мере зависят от правильной спецификации модели.
Рассмотрим два случая:
- отсутствие в модели переменной, которая должна быть включена;
- наличие в модели переменной, которая не должна быть включена.
Влияние отсутствия в модели переменной, которая должна быть включена
Предположим, что переменная y зависит от двух переменных x1 и x2 в соответствии с соотношением y = a + b1x1 + b2x2 + e. Однако считается, что модель выглядит как y = a + b1x1 + e, и оценивается регрессия 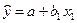 .
.
В этом случае оценка b1 и её дисперсия являются смещенными.
Смещенность оценки b1 связана с тем, что если не учесть x2 в регрессии, то переменная x1 будет играть двойную роль: отражать своё прямое влияние и заменять переменную x2 в описании её влияния.
Коэффициент R2 для данной регрессии отражает общую объясняющую способность переменной x1 в обеих ролях и является завышенной оценкой.
Влияние включение в модель переменной, которая не должна быть включена
Допустим, что истинная модель представляется в виде y = a + b1x1 + e.
Однако считается, что ею является y = a + b1x1 + b2x2 + e и оценивается регрессия 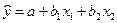 .
.
Оценки коэффициентов регрессии и их дисперсии в этом случае являются несмещенными, но неэффективными. Практически обнаруживается, что коэффициент b2 статистически незначим и переменная x2 исключается из модели.
Замещающие переменные
Предположим, что истинной моделью является
y = a + b1x1 + b2x2 + … + b k xk + e,
и допустим, что не имеется данных по существенной переменной x1.
Если не включить в модель эту переменную, то регрессия может пострадать от смещения оценок и статистическая проверка будет некорректной.
Если вместо отсутствующей переменной x1 использовать её заменитель z, линейно связанный с x1 и построить регрессию
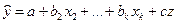 ,
,
то оценки b2, …, bk, их стандартные ошибки и коэффициент R2 будут такими же, как с использованием x1. Единственным недостатком является то, что отсутствует оценка коэффициента при самой величине x1, а величина a не является оценкой a.
В качестве замещающей переменной, например, для показателя технического прогресса может использоваться время.
Фиктивные переменные
При исследовании влияния качественных признаков в модель можно вводить фиктивные переменные, принимающие, как правило, два значения: единица, если данный признак присутствует в наблюдении, и ноль при его отсутствии.
Если включаемый в рассмотрение качественный признак имеет не два, а несколько значений, то используют несколько фиктивных переменных, число которых должно быть на единицу меньше числа значений признака.
При назначении фиктивных переменных исследуемая совокупность по числу значений качественного признака разбивается на группы. Одну из групп выбирают как эталонную (группа 0) и определяют фиктивные переменные для остальных.
Например, если качественный признак имеет три значения, то две фиктивные переменные определяются следующим образом:
- группа 0: z1 = z2 = 0,
- группа 1: z1 = 1, z2 = 0,
- группа 2: z1 = 0, z2 = 1,
или
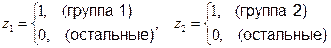
Введение в регрессию фиктивных переменных существенно улучшает качество ее оценивания.
Пример 4.3. Имеются данные о весе y новорожденного в граммах и количестве x сигарет, выкуриваемых в день будущей матерью во время беременности в случаях, когда рожала женщина до этого или нет.
| № | Первенец? | y | x | D | № | Первенец? | y | x | D |
| 1 | Нет | 3450 | 8 | 1 | 11 | Нет | 3200 | 31 | 1 |
| 2 | Нет | 3300 | 21 | 1 | 12 | Нет | 3400 | 13 | 1 |
| 3 | Нет | 3400 | 18 | 1 | 13 | Да | 3450 | 5 | 0 |
| 4 | Нет | 3300 | 24 | 1 | 14 | Да | 3400 | 10 | 0 |
| 5 | Нет | 3450 | 6 | 1 | 15 | Да | 3200 | 19 | 0 |
| 6 | Нет | 3450 | 16 | 1 | 16 | Да | 3350 | 12 | 0 |
| 7 | Нет | 3100 | 19 | 1 | 17 | Да | 3000 | 20 | 0 |
| 8 | Нет | 3500 | 7 | 1 | 18 | Да | 3300 | 8 | 0 |
| 9 | Нет | 3400 | 20 | 1 | 19 | Да | 3300 | 16 | 0 |
| 10 | Нет | 3500 | 10 | 1 | 20 | Да | 3400 | 9 | 0 |
Оценив регрессию между y и x, получим выражение:
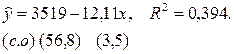
Это означает, что ребенок, рожденной некурящей матерью, будет иметь при рождении средний вес около 3500 г, и что уменьшение веса новорожденного по причине курения составляет около 12 г на каждую сигарету, выкуриваемую в день будущей матерью.
Для учета качественного фактора (родился ли ребенок первым или не первым) введем в модель фиктивную переменную:
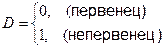 .
.
Оценив регрессию между y и x, D, получим выражение:
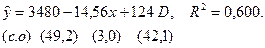
Коэффициент 124 при фиктивной переменной D статистически значим.
Это выражение можно переписать в виде двух уравнений:
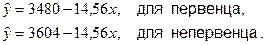
Параметр сдвига (эффект от фактора «первенец-непервенец») составляет 3604 – 3480 = 124 грамма.
Как видим, добавление в регрессию фиктивной переменной существенно улучшило качество оценки.
Лаговые переменные
При использовании данных временного ряда на текущие значения зависимой переменной могут влиять не только текущие значения объясняющих переменных, но также их значения с некоторым запаздыванием.
В общем, если какая-то переменная появляется в модели с запаздыванием на t периодов, она записывается с нижним индексом (t – t), например,
yt = b0 + b1xt + b2xt– t + e t.
Сдвиг t, характеризующий запаздывание в воздействии фактора на результат называется лагом. Переменная, влияние которой характеризуется некоторым запаздыванием, называется лаговой.
Дата: 2019-02-02, просмотров: 436.