Проверка гипотезы H0: b j = 0
Статистическая значимость коэффициентов множественной линейной регрессии с k объясняющими переменными проверяется на основе t-статистики:
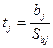 ,
,
имеющей распределение Стьюдента с n = n – k – 1 степенями свободы.
t-тесты для коэффициентов множественной регрессии выполняются так же, как и в парном регрессионном анализе. Отметим, что критический уровень t при любом уровне значимости зависит от числа степеней свободы, которое равно (n – k – 1): число наблюдений минус число оцененных параметров (один коэффициент для каждой независимой переменной и постоянный член). Доверительные интервалы определяются точно так же, как и в парном регрессионном анализе, в соответствии с указанием относительно числа степеней свободы.
t-статистика обеспечивает эффективную проверку значимости переменной при допущении, что все другие переменные уже включены в уравнение.
Последовательный отсев несущественных факторов составляет основу многошагового регрессионного анализа.
Однако на основе коэффициентов регрессии нельзя сказать, какой из факторов оказывает наибольшее влияние на зависимую переменную, т. к. коэффициенты регрессии между собой несопоставимы (они измерены разными единицами).
Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, рассчитываемые по формуле:
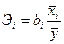 ,
,
где 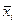 – среднее значение изучаемого фактора.
– среднее значение изучаемого фактора.
Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется зависимая переменная с изменением на 1 % каждого фактора при фиксированном значении других факторов.
Проверка гипотезы H0: b1 = b2 = … = b k = 0
Предположим, что в модель множественной регрессии включен свободный член, тогда TSS = ESS + USS, где ESS – объясняющая сумма квадратов отклонения с n1 = k числом степеней свободы, использованное на её объяснение, а USS – остаточная (необъясненная) сумма квадратов с n2 = n – k – 1 степенями свободы.
Для определения того, действительно ли объясненный разброс ESS больше случайного USS используется F-тест.
Построим F-статистику:
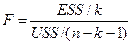
(для сопоставимости ESS и USS их значения привели на одну степень свободы).
После деления числителя и знаменателя этого выражения на TSS можно вычислить F-статистику на основе R2:
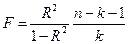 .
.
Показатели F и R2 равны или не равны нулю одновременно, поэтому принятие гипотезы H0: F = 0 равнозначно статистической незначимости R2.
Величина F имеет распределение Фишера с n1 = k, n2 = n – k – 1 степенями свободы. Наблюдаемому (расчетному) значению критерия F соответствует определенная значимость F, которую можно определить в Excel с помощью функции FРАСП(F; n1; n2).
Из сравнения значимости F с заданным стандартным уровнем значимости, получаем:
- если значимость F > стандартного уровня, то R2 незначим;
- если значимость F < стандартного уровня, то R2 значим.
Чаще всего F-тест используется для оценки того, значимо ли объяснение, даваемое уравнением в целом.
Проверка гипотезы H0: F = 0 равнозначно проверке гипотезы
H0: b1 = b2 = … = b k = 0
об одновременном равенстве нулю всех коэффициентов линейной регрессии, за исключением свободного члена.
Замечание. Если объясняющие способности независимых переменных перекрываются (сильная корреляция между ними), то t-тест для каждой переменной окажется незначим, в то время как F-тест для уравнения в целом вполне может быть значим.
Мультиколлинеарность
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. При наличии мультиколлинеарности МНК-оценки формально существуют, но обладают рядом недостатков:
1) небольшое изменение исходных данных приводит к существенному изменению оценок регрессии;
2) оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокое значение R2).
Если при оценке уравнения регрессии несколько факторов оказались незначимы, то нужно выяснить, нет ли среди них сильно коррелированных между собой.
При наличии корреляции один из пары связанных между собой факторов исключается либо в качестве объясняющего фактора берется какая-то их функция. Если статистически незначим лишь один фактор, то он должен быть исключен либо заменен другим показателем.
Для отбора факторов в модель регрессии и оценки их мультиколлинеарности можно использовать матрицу парных коэффициентов корреляции (расчет корреляционной матрицы можно выполнить в MS Excel).
В модель регрессии включаются те факторы, которые сильнее связаны с зависимой переменной, но слабо связанные с другими факторами.
Упражнение 4.2. Пусть по данным бюджетного обследования семи случайно выбранных семей изучалась зависимость накопления y от дохода x1, расходов на питание x2 и стоимости имущества x3. Исходные данные (усл. ед.):
| x1 | 40 | 55 | 45 | 30 | 30 | 60 | 50 |
| x2 | 10 | 15 | 12 | 8 | 10 | 20 | 15 |
| x3 | 60 | 40 | 40 | 15 | 90 | 30 | 30 |
| y | 2 | 7 | 5 | 4 | 2 | 7 | 6 |
Используя инструменты MS Excel, получите матрицу парных коэффициентов корреляции:
| y | x1 | х2 | x3 | |
| y | 1 | |||
| х1 | 0,85 | 1 | ||
| х2 | 0,81 | 0,93 | 1 | |
| х3 | –0,65 | –0,38 | –0,28 | 1 |
Проанализируйте целесообразность включения в модель каждого фактора.
Дата: 2019-02-02, просмотров: 423.