Для решения классической транспортной задачи с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности рассмотрим задачу оптимального планирования перевозок бензина некоторой марки между нефтеперерабатывающими заводами (НПЗ) и автозаправочными станциями (АЗС). В этом случае в качестве транспортируемого продукта рассматривается бензин, в качестве пунктов производства – 3 нефтеперерабатывающих завода (m = 3), а в качестве пунктов потребления – 4 автозаправочные станции n = 4). Объемы производства бензина следующие: НПЗ № 1 – 10 т, НПЗ № 2 – 14 т, НПЗ № 3 – 7 т. Объемы потребления бензина следующие: АЗС № 1 – 15 т, АЗС № 2 – 2 т, АЗС № 3 – 8,5 т, АЗС № 4 – 5,5 т. Стоимость транспортировки одной тонны бензина между НПЗ и АЗС задана в форме таблицы (табл. 3.9).
Таблица 3.9
Стоимость транспортировки бензина между НПЗ и АЗС
(в тыс. тенге)
Пункты
Производства
Пункты потребления
Соответствующая математическая постановка рассматриваемой транспортной задачи может быть записана в следующем виде:
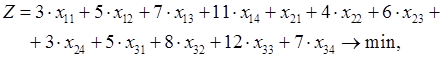 (1)
(1)
где множество допустимых альтернатив формируется следующей системой ограничений типа равенств:
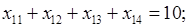
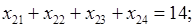
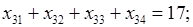
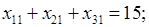 (2)
(2)
Примечание: Хотя в общем случае методы закрытых и открытых транспортных задач имеют некоторые отличия, с точки зрения решения этих задач с помощью программы М S Excel это не имеет принципиального значения. Поэтому в дальнейшем проверку условия сбалансированности можно вообще не принимать во внимание.
Для решения сформулированной транспортной задачи с помощью программы MS Excel выполним следующие подготовительные действия:
1. Внесем необходимые надписи в ячейки A 5: A 10, B 1, F 1, B 5: G 5, как это изображено на рис. 3.1. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой транспортной задачи.
2. В ячейки B 2: E 4 введем значения коэффициентов целевой функции (табл. 3.9).
3. В ячейку F 2 введем формулу: =СУММПРОИЗВ( B 2: E 4; B 6: E 8), которая представляет целевую функцию (1).
4. В ячейки G 6: G 8 и B 10: E 10 введем значения, соответствующие правым частям ограничений (2).
5. В ячейку F 6 введем формулу: =СУММ( B 6: E 6), которая представляет первое ограничение (2).
6. Скопируем формулу, введенную в ячейку F 6, в ячейки F 7 и F 8.
7. В ячейку B 9 введем формулу: =СУММ( B 6: B 8), которая представляет четвертое ограничение (2).
8. Скопируем формулу, введенную в ячейку B 9, в ячейки C 9, D 9 и E 9.
Внешний вид рабочего листа MS Office Excel с исходными данными для решения транспортной задачи показан на рис. 3.1.
Рис. 3.1. Исходные данные для решения транспортной задачи
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис Þ Поиск решения...
После появления диалогового окна Поиск решения следует выполнить следующее:
1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $ F $2.
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес диапазона ячеек $ B $2:$ E $4.
4. Добавить 7 ограничений, соответствующих базовым ограничениям исходной постановки решаемой транспортной задачи. С этой целью выполнить следующие действия:
· для задания первых трех ограничений в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
· в появившемся дополнительном окне выбрать ячейки F 6: F 8, которая должна отобразиться в поле с именем Ссылка на ячейку;
· в качестве знака ограничения из выпадающего списка выбрать строгое равенство «=»;
· в качестве значений правой части ограничения выбрать ячейки G 6: G 8;
· для добавления следующих ограничений в дополнительном окне нажать кнопку с надписью Добавить;
· в появившемся дополнительном окне выбрать ячейки B 9: E 9, которая должна отобразиться в поле с именем Ссылка на ячейку;
· в качестве знака ограничения из выпадающего списка выбрать строгое равенство «=»;
· в качестве значений правой части ограничения выбрать ячейки B 10: E 10.
5. Добавить последнее ограничение на неотрицательность значений переменных задачи.
Внешний вид диалогового окна мастера поиска решения с ограничениями для транспортной задачи изображен на рис. 3.2.
6. В дополнительном окне Параметры поиска решения следует выбрать отметки Линейная модель и Неотрицательные значения (рис. 3.3).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить.
Рис. 3.2. Параметры мастера поиска решения и базовые ограничения
для транспортной задачи
Рис. 3.3. Параметры поиска решения
После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид (рис. 3.4).
Рис. 3.4. Результат количественного решения транспортной задачи
Результатом решения транспортной задачи являются найденные оптимальные значения переменных:
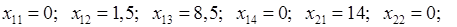
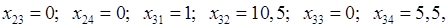
которым соответствует значение целевой функции: ¦опт = 208,5. При выполнении расчетов для ячеек B 6: E 8 был выбран числовой формат с тремя знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения потребностей АЗС № 1 следует транспортировать 14 т бензина из НПЗ № 2 и 1 т – из НПЗ № 3; для удовлетворения потребностей АЗС № 2 следует транспортировать 1,5 т бензина из НПЗ № 1 и 10,5 т – из НПЗ № 3; для удовлетворения потребностей АЗС № 3 следует транспортировать8,5 т бензина из НПЗ № 1 и, наконец, для удовлетворения потребностей АЗС № 4 следует транспортировать 5,5 т бензина из НПЗ № 3. При этом общая стоимость найденного плана перевозок составит 208,5 тыс. тенге.
Дата: 2019-02-02, просмотров: 379.