Рассмотрим систему s линейных уравнений с n неизвестными
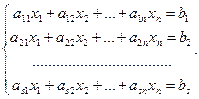 (6.1)
(6.1)
1. Если среди уравнений системы есть уравнения вида 0x1+0x2+...+0xn=bk , где bk ¹0, то система уравнений (6.1) несовместна.
2. Пусть в каждом уравнении системы есть хотя бы по одному отличному от 0 коэффициенту. Если a11 =0, то перенумерацией неизвестных добьемся, чтобы первый коэффициент был отличен от нуля. Таким образом, можем считать , что a11¹0.
Исключим теперь слагаемые, содержащие х1, из всех остальных уравнений. Для этого к каждому i-ому (i=2,...,n) уравнению прибавим первое, умноженное на 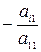 (i=2,...,n).
(i=2,...,n).
продолжим аналогичные рассуждения для переменной х2 (начиная со второго уравнения).
Если в системе уравнений в результате преобразований появились уравнения вида 0x1+0x2+...+0xn=0, то их отбрасываем, а если появилось уравнение вида 0x1+0x2+...+0xn=bk , где bk ¹0, то полученная система уравнений , а следовательно и равносильная ей система уравнений (6.1), несовместна.
Если система не содержит уравнений вида 0x1+0x2+...+0xn=bk , где bk ¹0, то будем считать, что a22 ¹0, и исключим х2 из всех оставшихся уравнений, прибавляя к каждому i-ому (i=3,...,n) уравнению второе, умноженное на 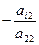 (i=3,...,n). Так как система содержит конечное число уравнений, то процесс исключения неизвестных конечен. То есть через некоторое число шагов мы получим систему уравнений
(i=3,...,n). Так как система содержит конечное число уравнений, то процесс исключения неизвестных конечен. То есть через некоторое число шагов мы получим систему уравнений
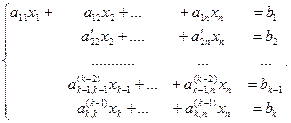 (6.2)
(6.2)
Здесь 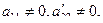 ...,
..., 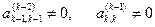 , k £s, и, очевидно, k £n.
, k £s, и, очевидно, k £n.
В этом случае система уравнений (6.2) и, следовательно, система уравнений (6.1) совместны, причем, если k=n, то система имеет единственное решение, а если k <n ,то система уравнений имеет бесконечное множество решений.
Действительно, если k=n, то система имеет вид
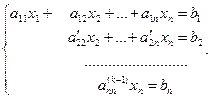 (6.3)
(6.3)
Так как 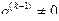 , то из последнего уравнения системы (6.3) найдем xn, подставим найденное значение во все остальные уравнения системы и из предпоследнего уравнения найдем xn-1 и так далее. Все переменные определяются однозначно и система (6.3) и, следовательно, система уравнений (6.1) имеют единственное решение.
, то из последнего уравнения системы (6.3) найдем xn, подставим найденное значение во все остальные уравнения системы и из предпоследнего уравнения найдем xn-1 и так далее. Все переменные определяются однозначно и система (6.3) и, следовательно, система уравнений (6.1) имеют единственное решение.
Если k <n, то система уравнений имеет вид (6.3). Неизвестные хk+1, xk+2, ..., xn объявляем свободными. Этим переменным можно присвоить любые значения и поднимаясь по системе (6.3) снизу вверх, найти значения остальных переменных, которые для данного набора свободных переменных определяются однозначно. Таким образом, давая различные значения свободным переменным хk+1, xk+2,...,xn, получим все решения системы.
Вывод . Метод Гаусса применим к решению любой системы линейных уравнений. При этом система (6.1) будет несовместной, если в процессе преобразований получится уравнение вида 0x1+0x2+...+0xn=bk , где bk ¹0, или система будет совместной. Совместная система имеет единственное решение, если k=n, и будет иметь множество решений, если k <n.
Замечание 1. Однородная система уравнений всегда совместна, так как в ней не может быть уравнений вида 0x1+0x2+...+0xn=bk , где bk ¹0. Она всегда имеет нулевое решение, а если k <n,то система имеет и ненулевые решения.
Замечание 2. На практике все преобразования производят не над уравнениями системы, а над строками расширенной матрицы системы.
Если b1=b2=…=bs=0, тогда система линейных уравнений имеет вид
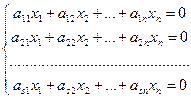 (6.4)
(6.4)
и называется однородной. Очевидно, что однородная система всегда совместна, то есть множество ее решений не пусто. В частности, решением любой однородной системы линейных уравнений будет решение: x1=…=xn=0. Это решение называется нулевым, или тривиальным.
Пример выполнения заданий практической части
Пример 1. Решить систему линейных уравнений
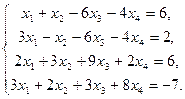
Решение. Выпишем расширенную матрицу системы и приведем ее к диагональному виду
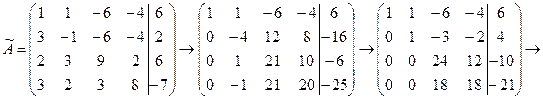

Таким образом, получили следующее решение системы линейных уравнений
х1=0, х2=2, х3=1/3, х4=-1,5.
Пример 2. Решить систему линейных уравнений
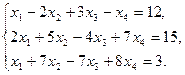
Решение. Составим расширенную матрицу системы и приведем ее к диагональному виду
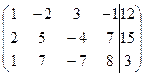 ~
~  ~
~ 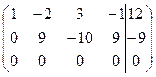
Матрица приведена к диагональному виду, запишем соответствующую систему линейных уравнений
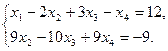
Данная система имеет бесконечно много решений. Чтобы найти общее решение переменные х3 и х4 объявим свободными, а остальные выразим через свободные, получим
 следовательно
следовательно
x3=c1, x4=c2, x2= 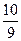 c1-c2-
c1-c2-  , x1=
, x1= 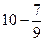 с1-с2
с1-с2
Таким образом, общее решение системы имеет вид:
( 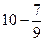 с1-с2,
с1-с2,  c1-c2-
c1-c2-  , с1, с2), где с1 и с2 – произвольные действительные числа. Если дать свободным переменным некоторые значения, получим частные решения системы.
, с1, с2), где с1 и с2 – произвольные действительные числа. Если дать свободным переменным некоторые значения, получим частные решения системы.
Пример 3. Решить систему уравнений
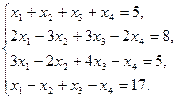 (*)
(*)
Решение. Составим расширенную матрицу системы и приведем ее к диагональному виду
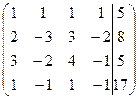 ~
~ 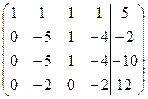 ~
~ 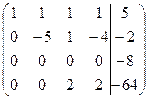
Третья строка соответствует уравнению
0x1+0x2+0x3+0x4=-8, которое не имеет решений, следовательно, система (*) также не имеет решений.
Пример 4. Решить систему линейных однородных уравнений
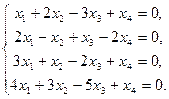 (
( 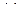 )
)
Решение. Будем решать систему методом Гаусса. Выпишем расширенную матрицу системы и упростим ее.
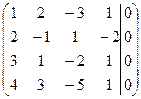 ~
~ 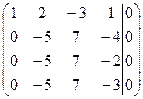 ~
~ 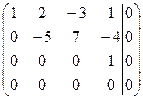 ~
~ 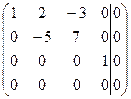
Получили систему, равносильную данной
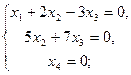 Û
Û 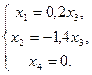 .
.
Система линейных уравнений имеет бесчисленное множество решений. Общее решение имеет вид (0,2с; -1,4с; с; 0).
Пример 5. Решить систему линейных однородных уравнений
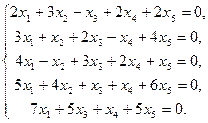
Решение. Будем решать систему методом Гаусса. Выпишем расширенную матрицу системы и упростим ее.
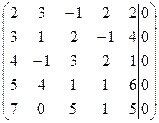 ~
~ 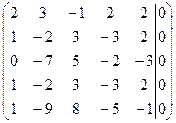 ~
~ 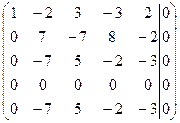 ~
~
~ 
Получили систему, равносильную данной
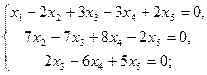 Û
Û 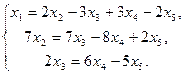
Переменные х4 и х5 объявляем свободными. Пусть х4=с1, х5=с2, тогда
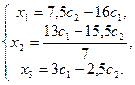
Общее решение системы имеет вид
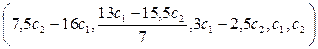
Пример 6. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
| Тип | Способ раскроя | ||
| заготовки | 1 | 2 | 3 |
| А | 3 | 2 | 1 |
| Б | 1 | 6 | 2 |
| В | 4 | 1 | 5 |
Записать в математической форме условия выполнения задания.
Решение. Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3x заготовок типа А, при втором - 2y, при третьем - z. Для полного выполнения задания по заготовкам типа А сумма 3x +2y +z должна равняться 360, т.е.
3x +2y + z =360.
Аналогично получаем уравнения
x + 6y +2z = 300
4x + y + 5z = 675,
которым должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В. Решим систему методом Гаусса. Запишем расширенную матрицу системы и приведем ее с помощью элементарных преобразований к диагональному виду.
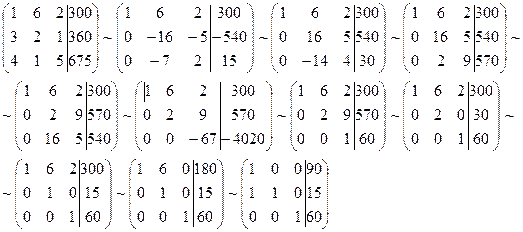
Следовательно, x = 90, y = 15, z = 60.
Задания для аудиторного занятия
1. Решить системы линейных уравнений:
1.1.  1.2.
1.2. 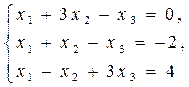
1.3. 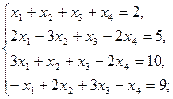 1.4.
1.4. 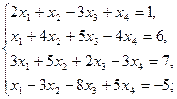
1.5.  1.6.
1.6. 
1.7. 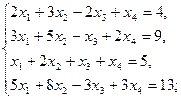 1.8.
1.8. 
1.9. 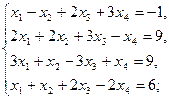 1.10.
1.10. 
1.11.  1.12.
1.12. 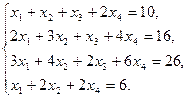
2. На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов. Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.
| Изделие | Выход из единицы сырья | |||
| способ | I | II | III | IV |
| А | 2 | 1 | 7 | 4 |
| Б | 6 | 12 | 2 | 3 |
3. Решить однородные системы линейных уравнений.
3.1. 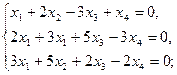 3.2.
3.2. 
3.3. 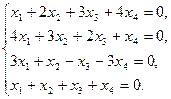
1.13
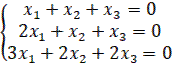
1.14 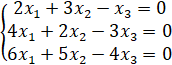
1.15 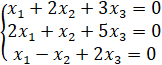
1.16 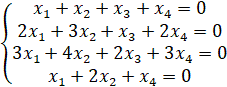
1.17 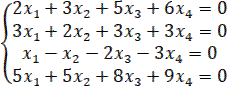
1.18 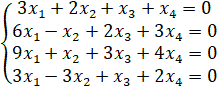
1.19 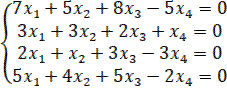
1.20 
1.21 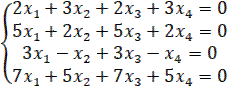
1.22 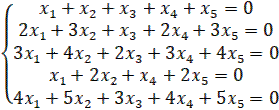
1.23 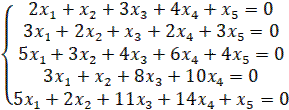
1.24 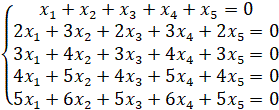
6.4. Домашнее задание
1. Решить системы линейных уравнений:
1.1.  1.2.
1.2. 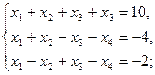
1.3. 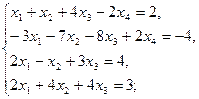 1.4.
1.4. 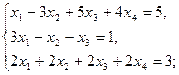
1.5. 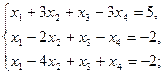 1.6.
1.6. 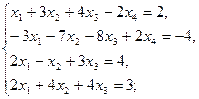
1.7. 
2. Решить однородные системы линейных уравнений.
2.1. 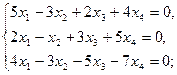 2.2.
2.2. 
2.3. 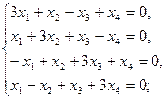 2.4.
2.4. 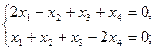
2.5. 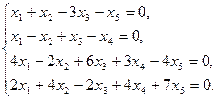
3. На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов. Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.
| Изделие | Выход из единицы сырья | |||
| способ | I | II | III | IV |
| А | 2 | 1 | 7 | 4 |
| Б | 6 | 12 | 2 | 3 |
Дата: 2019-02-02, просмотров: 357.