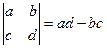
2. Вычисление определителей третьего порядка по определению (правило треугольника).

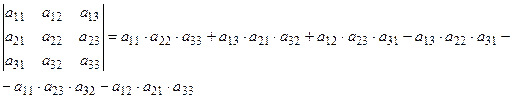
Данную формулу можно наглядно изобразить с помощью схемы:

 3. Приведение определителя к треугольному виду.

Будем говорить, что определитель приведен к треугольному виду, если 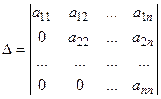. Значение такого определителя равно произведению элементов главной диагонали, то есть .

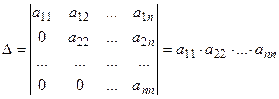Достигается такой вид определителя с помощью следующих элементарных преобразований:

- вынесение общего множителя всех элементов некоторой строки (столбца) определителя за знак определителя;

- сложение некоторой строки (столбца) определителя с другой строкой (столбцом), возможно умноженной на отличное от нуля число;

- транспозиция строк (столбцов) определителя с переменой знака определителя.

4. Разложение определителя по элементам некоторых строк (столбцов).

В основе этого метода лежит теорема Лапласа.

Сформулируем необходимые определения.

Определение. Если в определителе n-го порядка выбрать произвольно k строк и k столбцов, то элементы, стоящие на пересечении указанных строк и столбцов, образуют квадратную матрицу порядка k. Определитель такой квадратной матрицы называют минором k-го порядка. Обозначается M_k .

Если k=1, то минор первого порядка - это элемент определителя. Элементы, стоящие на пересечении оставшихся (n-k) строк и (n-k) столбцов, составляют квадратную матрицу порядка (n-k). Определитель такой матрицы называется минором, дополнительным к минору M_k (Обозначается M_n-k).

Определение. Алгебраическим дополнением минора M_k  будем называть его дополнительный минор, взятый со знаком “+” или “-” в зависимости от того, четна или нечетна сумма номеров всех строк и столбцов, в которых расположен минор M_k.

Если k=1, то алгебраическое дополнение к элементу a_ik вычисляется по формуле

A_ik=(-1)^i+kM_ik, где M_ik - минор (n-1) порядка.

Теорема (Лапласа). Если в определителе n-го порядка выбрать произвольно k строк (или k столбцов), 1£k£n-1, тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна значению определителя D.

Следствие 1. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения равна значению определителя.

Следствие 2. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения к элементам другой строки равна нулю.