Метод основан на следствии из теоремы Лапласа и заключается в следующем:
1. - с помощью элементарных преобразований получить в некоторой строке (столбце) определителя n-1 нулевой элемент (все, кроме одного);
2. - разложить определитель по элементам полученной строки (столбца);
3. - в результате применения следствия из теоремы Лапласа получится определитель порядка n-1 (на 1 меньше, чем порядок исходного);
4. - повторять указанные действия до тех пор, пока получится определитель третьего или второго порядка;
5. - полученный определитель вычислить одним из указанных выше способов.
Пример выполнения заданий практической части
Пример 1. Найти значение определителя, пользуясь правилом треугольника: 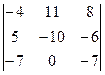 .
.
Решение.
Для вычисления значения определителя воспользуемся формулой 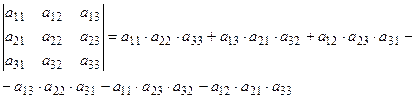 .
.
Получаем:
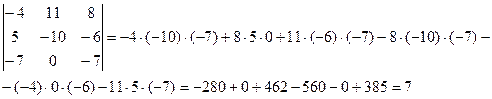
Пример 2. Найти значение определителя методом приведения к треугольному виду: 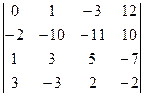 .
.
Решение.
Для приведения определителя к треугольному виду воспользуемся элементарными преобразованиями.
Сначала получим а11=1.
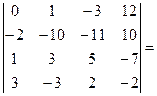 [поменяем местами первый и второй столбец, поменяв при этом знак перед определителем]= –
[поменяем местами первый и второй столбец, поменяв при этом знак перед определителем]= – 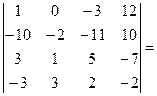 [будем получать нули в первом столбце; умножим первую строку на 10 и сложим со второй] =
[будем получать нули в первом столбце; умножим первую строку на 10 и сложим со второй] =
= – 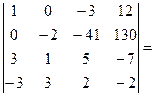 [умножим первую строку на 3 и вычтем из третьей] =
[умножим первую строку на 3 и вычтем из третьей] =
= - 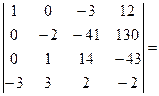 [умножим первую строку на 3 и сложим с четвертой]=
[умножим первую строку на 3 и сложим с четвертой]=
= – 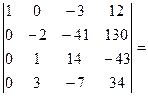 [поменяем местами вторую и третью строки, поменяв знак перед определителем]=
[поменяем местами вторую и третью строки, поменяв знак перед определителем]= 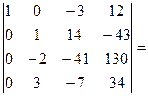 [ будем получать нули во втором столбце; умножим вторую строку на 2 и сложим с третьей]=
[ будем получать нули во втором столбце; умножим вторую строку на 2 и сложим с третьей]= 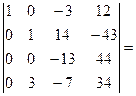 [умножим вторую строку
[умножим вторую строку
на 3 и вычтем из четвертой]= 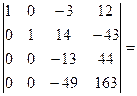 [умножим третью строку на 4 и вычтем из четвертой] =
[умножим третью строку на 4 и вычтем из четвертой] = 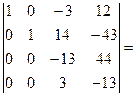 [умножим четвертую строку на 4 сложим с третьей]=
[умножим четвертую строку на 4 сложим с третьей]= 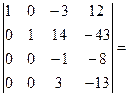 [умножим третью строку на 3 и сложим с четвертой]= =
[умножим третью строку на 3 и сложим с четвертой]= = 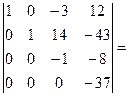 [определитель приведен к треугольному виду; найдем произведение элементов главной диагонали]=37.
[определитель приведен к треугольному виду; найдем произведение элементов главной диагонали]=37.
Пример 3. Найти значение определителя, разложив его по элементам первой и третьей строки: 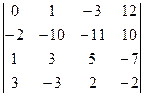 .
.
Решение.
Для вычисления значения определителя, воспользуемся теоремой Лапласа. Так как указано две строки, а данный определитель четвертого порядка, то и миноры, и их алгебраические дополнения будут являться определителями второго порядка. Получаем:
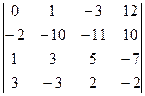 =
= 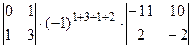 +
+ 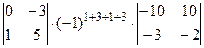 +
+
+ 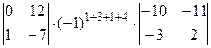 +
+ 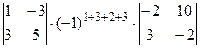 +
+
+ 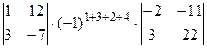 +
+ 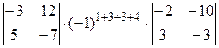 = (0×3-1×1) ×(-1)7×(-11×(-2)-10×2)+(0×5-(-3) ×1) ×(-1)8×(-10×(-2)-10×(-3))+(0×(-7)-12×1) ×(-1)9(-10×2-(-11) ×(-3))+(1×5-(-3) ×3)
= (0×3-1×1) ×(-1)7×(-11×(-2)-10×2)+(0×5-(-3) ×1) ×(-1)8×(-10×(-2)-10×(-3))+(0×(-7)-12×1) ×(-1)9(-10×2-(-11) ×(-3))+(1×5-(-3) ×3)
×(-1)9×(-2×(-2)-10×3)+(1×(-7)-13×3) ×(-1)10×(-2×2-(-11) ×3)+(-3×(-7)-12×5) ×(-1)11(-2×(-3)-(-10) ×3) = (-1)×(-1) ×2+3×50+(-12) ×(-1) ×(-53)+14×(-1) ×(-26)+(-43) ×29+(-39) ×(-1) ×36=37.
Пример 4. Найти значение определителя методом понижения порядка: 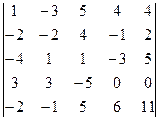 .
.
Решение.
Для того чтобы воспользоваться следствием теоремы Лапласа, получим нули, например, в первом столбце.
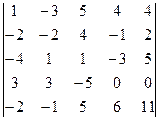 =[умножим первую строку на 2 и сложим со второй]= =
=[умножим первую строку на 2 и сложим со второй]= = 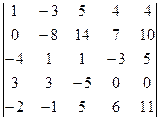 =[умножим первую строку на 4 и сложим с третьей]= =
=[умножим первую строку на 4 и сложим с третьей]= = 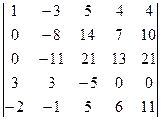 =[умножим первую строку на 3 и вычтем из четвертой]= =
=[умножим первую строку на 3 и вычтем из четвертой]= = 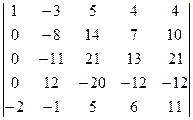 =[умножим первую строку на 2 и сложим с пятой]=
=[умножим первую строку на 2 и сложим с пятой]=
= 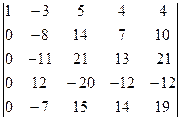 =[разложим определитель по элементам первого столбца, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
=[разложим определитель по элементам первого столбца, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]= 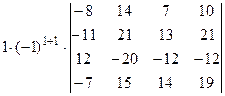 =[вынесем за знак определителя из третьей строки множитель (-4)]=
=[вынесем за знак определителя из третьей строки множитель (-4)]= 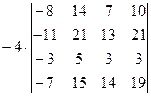 =[вынесем за знак определителя из первого столбца множитель (-1)]=
=[вынесем за знак определителя из первого столбца множитель (-1)]= 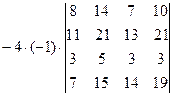 =[вычтем из первой строки четвертую, чтобы получить единицу в первой строке]=
=[вычтем из первой строки четвертую, чтобы получить единицу в первой строке]= 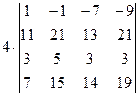 =[в данном случае удобнее получать нули в первой строке, поэтому сложим первый столбец со вторым]= =
=[в данном случае удобнее получать нули в первой строке, поэтому сложим первый столбец со вторым]= = 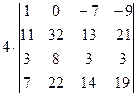 =[умножим первый столбец на 7 и сложим с третьим]= =
=[умножим первый столбец на 7 и сложим с третьим]= = 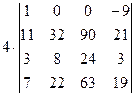 =[ умножим первый столбец на 9 и сложим с четвертым]= =
=[ умножим первый столбец на 9 и сложим с четвертым]= = 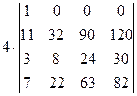 =[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
= 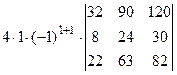 =
= 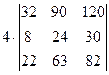 =[вынесем из первой строки множитель 2]= =
=[вынесем из первой строки множитель 2]= = 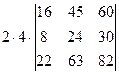 =
= 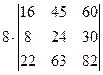 =[вынесем из второй строки множитель 2]=
=[вынесем из второй строки множитель 2]= 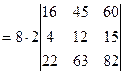 =[вынесем из первого столбца множитель 2]= =
=[вынесем из первого столбца множитель 2]= = 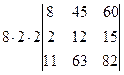 =
= 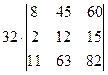 =[вынесем из второго столбца множитель 3]= =
=[вынесем из второго столбца множитель 3]= = 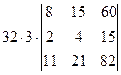 =[вторую строку умножим на 4 и вычтем из первой]= =
=[вторую строку умножим на 4 и вычтем из первой]= = 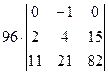 =[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме второго, будут равны нулю]=
=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме второго, будут равны нулю]= 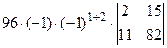 =96×(2×82-11×15)=-96.
=96×(2×82-11×15)=-96.
Задания для аудиторного занятия
1. Вычислить определители с помощью правила треугольников:
1.1. 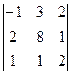 ; 1.2.
; 1.2. 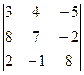 ..
.. 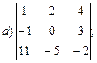
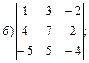
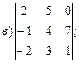 1.2
1.2 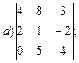
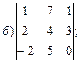
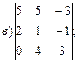
2. Решить уравнения:
2.1. 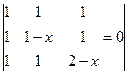 ; 2.2.
; 2.2. 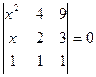 .
.
3. Вычислить определитель, разложив его по элементам:
3.1. 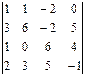 4-го столбца; 3.2.
4-го столбца; 3.2. 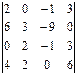 3-ей строки.
3-ей строки.
4. Вычислить определители методом приведения к треугольному виду:
4.1. 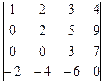 ; 4.2.
; 4.2. 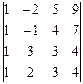 .
.
5. Вычислить определители:
5.1. 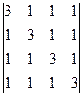 ; 5.2.
; 5.2. 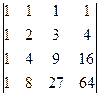
5.3. 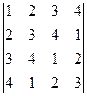 .
. 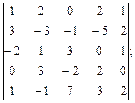 4.2.
4.2. 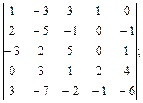 4.3.
4.3. 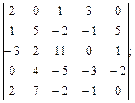
4.4. 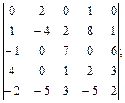 4.5.
4.5. 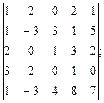 4.6.
4.6. 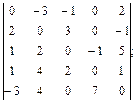
4.7. 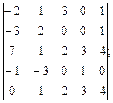 4.8.
4.8. 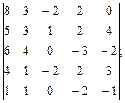 4.9.
4.9. 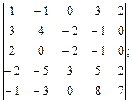
2.4. Домашнее задание
1. Вычислить определители с помощью правила треугольников:
1.1. 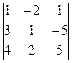 ; 1.2.
; 1.2. 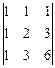 .
.
2. Вычислить определитель, разложив его по элементам:
2.1. 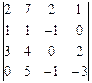 4-ой строки; 2.2.
4-ой строки; 2.2. 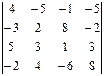 3-его столбца.
3-его столбца.
3. Вычислить определители:
3.1. 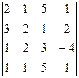 ; 3.2.
; 3.2. 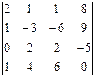 ;
;
3.3. 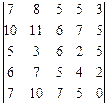
Дата: 2019-02-02, просмотров: 375.