Определение. Рангом матрицы называют максимальное числу ее линейно независимых строк (столбцов). Обозначение: rangA или r(A).
Свойства ранга:
1. Ранг нулевой матрицы считается равным нулю.
2.  .
.
3.  у матрицы
у матрицы 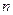 -го порядка тогда и только тогда, когда
-го порядка тогда и только тогда, когда 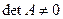 .
.
Ранг матрицы находится либо методом окаймляющих миноров, либо методом элементарных преобразований.
Теорема о ранге матрицы: Ранг матрицы равен наивысшему порядку отличных от нуля миноров этой матрицы.
Алгоритм №1 вычисления ранга матрицы
(метод окаймления миноров).
1) Если все элементы матрицы равны 0, то rang A=0. Если в матрице есть элементы, отличные от 0, то вычисляем миноры 2-го порядка.
2) Если все миноры 2-го порядка равны 0, то rang A=1. Если нашелся минор 2-го порядка, отличный от 0, то вычисляем миноры 3-го порядка, окаймляющие найденный ненулевой минор 2-го порядка.
3) Если все такие миноры 3-го порядка равны 0, то rang A=2. Если найдется минор 3-го порядка, отличный от 0, то вычисляем миноры 4-го порядка,
окаймляющие найденный ненулевой минор 3-го порядка и т.д.
4) Если найден минор k-го порядка, отличный от нуля, а все миноры (k+1)-го порядка, окаймляющие найденный ненулевой минор k-го порядка, равны нулю, то ранг матрицы равен k.
Определение. Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число,
4) транспонирование матрицы.
Теорема. Элементарные преобразования не меняют ранга матрицы.
Определение. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Алгоритм №2 вычисления ранга матрицы
(метод элементарных преобразований).
1. С помощью элементарных преобразований получить а11=1.
2. С помощью элементарных преобразований получить аi1=0, i¹1 ( все элементы первого столбца, кроме первого, равны 0).
3. Выполнить пункты 1 и 2 алгоритма для элементов второго столбца.
4. продолжать алгоритм до тех пор, пока матрица не будет приведена к ступенчатому виду:
 .
.
5. Ранг полученной ступенчатой матрицы А¢ будет равен числу ненулевых элементов на главной диагонали и равен рангу исходной матрицы. rangA = rangA¢ =  .
.
Строки (столбцы) матрицы  называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 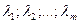 не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:  , где
, где 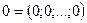 . В противном случае строки матрицы называются линейно независимыми.
. В противном случае строки матрицы называются линейно независимыми.
Пример выполнения заданий практической части
Пример 1. Найти методом окаймления миноров ранг матрицы
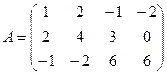 .
.
Решение . Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
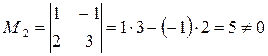 .
.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
добавить второй столбец или четвертый). Вычисляем их:
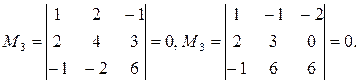
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум: 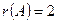 .
.
Пример 2. Найти ранг матрицы с помощью элементарных преобразований:
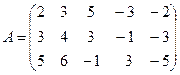 .
.
Решение . Из второй строки вычтем первую и переставим эти строки
 .
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
 ;
;
из третьей строки вычтем первую, получим матрицу
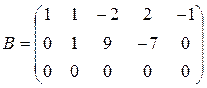 ,
,
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2.
Пример 3. Выяснить, при каком значении параметра 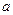 матрица имеет 3 линейно независимые строки:
матрица имеет 3 линейно независимые строки:  .
.
Решение. Матрица 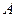 имеет три линейно независимые строки, если ее ранг равен 3, т.е.
имеет три линейно независимые строки, если ее ранг равен 3, т.е. 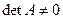 . Вычислим определитель матрицы:
. Вычислим определитель матрицы:
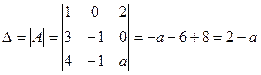 ,
,
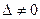 , т.е.
, т.е. 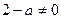 ;
; 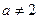 .
.
Следовательно, при всех значениях 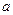 , кроме
, кроме  , все строки линейно независимы.
, все строки линейно независимы.
Пример 4. Определить максимальное число линейно независимых строк (столбцов) матрицы: 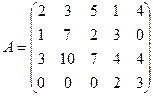 .
.
Решение. С помощью элементарных преобразований, не меняющих ранга матрицы, приведем ее к ступенчатому виду:
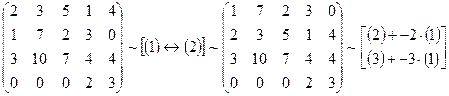 ~
~ 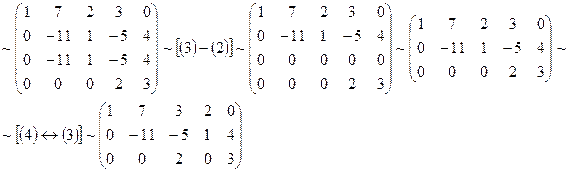
Значит, ранг матрицы 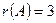 и исходная матрица имеет 3 линейно независимые строки (или столбца).
и исходная матрица имеет 3 линейно независимые строки (или столбца).
Задания для аудиторного занятия
1. Найти методом окаймления миноров ранг матрицы:
1.1.  ; 1.2.
; 1.2. 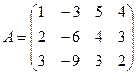 ;
;
1.3. 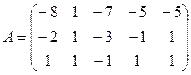 ; 1.4.
; 1.4. 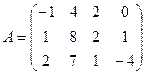 .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1. 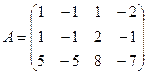 ; 2.2.
; 2.2. 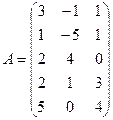 ;
;
2.3. 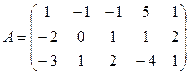 ; 2.4.
; 2.4. 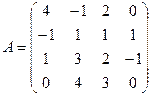 ;
;
2.5. 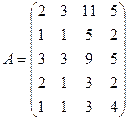 ; 2.6.
; 2.6. 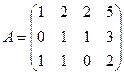 .
.
3. Найти максимальное число линейно независимых строк матриц:
3.1. 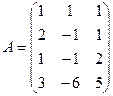 ; 3.2.
; 3.2. 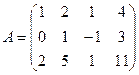 ;
;
3.3. 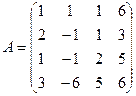 ; 3.4.
; 3.4. 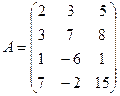 .
.
4.4. Домашнее задание
1. Найти методом окаймления миноров ранг матрицы:
1.1. 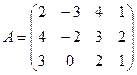 ; 1.2.
; 1.2. 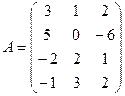 ;
;
1.3.  .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1.  ; 2.2.
; 2.2. 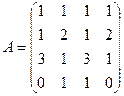 ;
;
2.3.  .
.
3. Найти максимальное число линейно независимых столбцов матриц:
3.1. 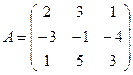 ; 3.2.
; 3.2. 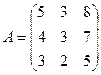 .
.
Дата: 2019-02-02, просмотров: 366.