Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. Американским экономистом В.Леонтьевым.
Введем следующие обозначения:
xi – общий объем продукции i-й отрасли (валовый выпуск);
xij – объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства;
yi – объем конечного продукта i-й отрасли для непроизводственного потребления.
Т.к. валовый объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то
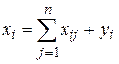 , i=1;2;…;n (5.5)
, i=1;2;…;n (5.5)
Уравнения (5.5) называются соотношениями баланса. Введем коэффициенты прямых затрат
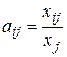 ,
,  i,j = 1;2;…n (5.6)
i,j = 1;2;…n (5.6)
показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.
Тогда соотношения баланса (5.5) примут вид 
xi= 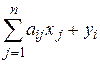
 i=1;2;…n (5.7)
i=1;2;…n (5.7)
Обозначим:
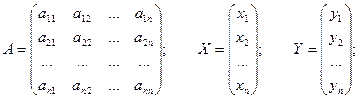
где X - вектор валового выпуска, Y- вектор конечного продукта, A - матрица прямых затрат.
Тогда (5.7) можно записать в матричном виде
X = AX + Y. (5.8)
Соотношение (5.8) называют уравнением линейного межотраслевого баланса. Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X , который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Перепишем систему (5.8) с использованием единичной матрицы Е в виде
( E – A )X = Y. (5.9)
Если матрица (Е – А) невырожденная, то существует обратная матрица ( Е – А )-1 и тогда существует единственное решение (5.8)
X = ( E – A )-1Y. (5.10)
Матрица ( Е –А )-1 называется матрицей полных затрат.
Матрица А≥0 называется продуктивной, если для любого вектора Y≥0 существует решение X≥0 уравнения (5.8).
Существует несколько критериев продуктивности матрицы А:
1. Матрица А продуктивна тогда и только тогда, когда матрица ( Е –А )-1 существует и ее элементы неотрицательны.
2. Матрица А с неотрицательными элементами продуктивна, если максимум сумм элементов по любому ее столбцу (строке) не превосходит единицы, причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.
Пример выполнения заданий практической части
Пример 1. Исследовать систему уравнений на совместность:
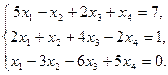
Решение. Выписываем расширенную матрицу системы:
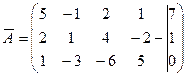
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу
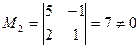
содержащие его миноры третьего порядка равны нулю:
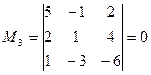 ;
; 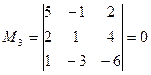
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы 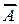 рассмотрим окаймляющий минор
рассмотрим окаймляющий минор
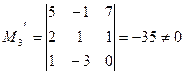
Значит, ранг расширенной матрицы r( 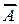 ) = 3. Поскольку r(A) ≠ r(
) = 3. Поскольку r(A) ≠ r( 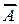 ), то система несовместна.
), то система несовместна.
Пример 2. Решить систему матричным способом: 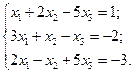
Решение .
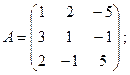
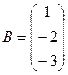 .
.
А×Х = В; Х = А-1 × В.
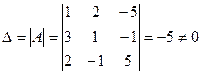 .
.
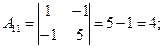
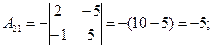
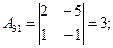
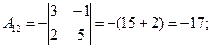
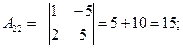
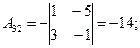
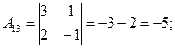
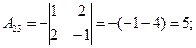
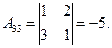
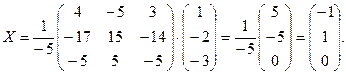
Пример 3. Решить систему уравнений, воспользовавшись формулами Крамера (4.4):
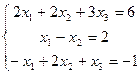
Решение.
1) Определитель данной системы 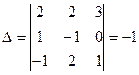 .
.
2) Найдем определитель 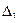 , заменив в определителе D первый столбец, столбцом свободных членов:
, заменив в определителе D первый столбец, столбцом свободных членов: 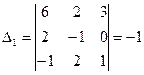 .
.
3) Найдем определитель 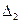 , заменив в определителе D второй столбец, столбцом свободных членов:
, заменив в определителе D второй столбец, столбцом свободных членов: 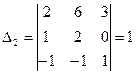 .
.
4) Найдем определитель 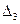 , заменив в определителе D третий столбец, столбцом свободных членов:
, заменив в определителе D третий столбец, столбцом свободных членов: 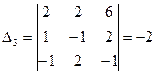 .
.
5) Найдем решения системы, воспользовавшись формулами Крамера (4.4):
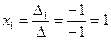 ;
; 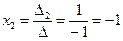 ;
; 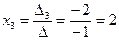 .
.
Ответ: (1, -1, 2).
Пример 4. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 1/3 вклада, который составляет 600 ден. ед., вложили в первый банк, а оставшуюся часть вклада во второй банк. К концу года сумма этих вкладов стала равна 700 ден. ед. Если бы первоначально 1/3 вклада положили во второй банк, а оставшуюся часть вклада - в первый банк, то к концу года сумма этих вкладов стала бы равна 680 ден. ед.
а) Записать в математической форме условия вложения денег.
б) Какой процент начисляет каждый банк?
Решение. Пусть x 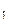 – процентная ставка начисления I-го банка, x
– процентная ставка начисления I-го банка, x 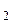 – процентная ставка начисления II-го банка. Тогда
– процентная ставка начисления II-го банка. Тогда
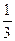 вклада в I банк составит:
вклада в I банк составит: 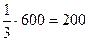 д.е.
д.е.
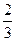 вклада в I банк составит:
вклада в I банк составит: 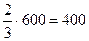 д.е.
д.е.
Так как к концу года суммы этих вкладов составили 700 д.е. в I-м банке и 680 д.е. во 2-м банке. Составим систему уравнений:
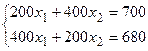 .
.
Решим систему по формулам Крамера:
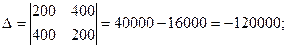
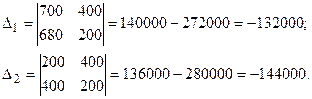
Тогда 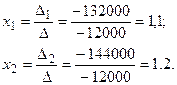
Таким образом, процентная ставка I-го банка составляет 10% и II-го банка 20%.
Пример 5. В таблице приведены данные об исполнении баланса за отчетный период.
|
отрасль | потребление | конечный продукт | валовый выпуск | ||
| энергетика | машино- строение | ||||
| производство | энергетика машиностроение | 7 12 | 21 15 | 72 123 | 100 150 |
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне.
Решение . По условию имеем матрицу-столбец конечного продукта

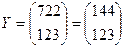
Валовый выпуск: x1=100; x2=150.
Объем продукции: x11=7; x12=21;
x21=12; x22=15.
По формуле 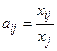 , находим
, находим
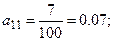
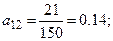
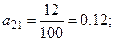
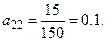
Т.е. матрица прямых затрат примет вид
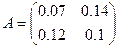 .
.
Полученная матрица имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
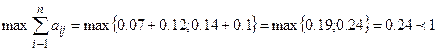 .
.
Необходимый объем валового выпуска X найдем по формуле: X = (E – A)-1Y.
Найдем матрицу полных затрат
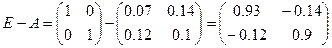
Т.к. 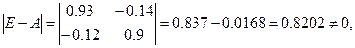
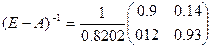 ,
,
тогда 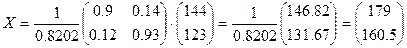 .
.
Т.е. валовый выпуск в энергетической отрасли надо увеличить до 179 усл.ед., а в машиностроительной – до 160.5 усл.ед..
Задания для аудиторного занятия
1. Проверить совместность систем уравнений (по теореме Кронекера–Капелли):
1.1. 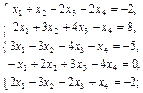 1.2.
1.2. 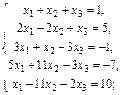
1.3. 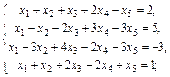 1.4.
1.4. 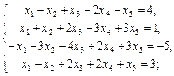
1.5. 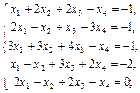 1.6.
1.6. 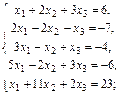
2. Решить системы линейных уравнений:
а) методом обратной матрицы;
б) по формуле Крамера.
2.1. 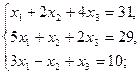 2.2.
2.2. 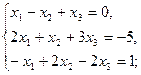
2.3. 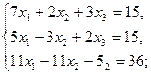 2.4.
2.4. 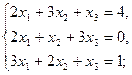
2.5. 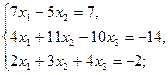 2.6.
2.6. 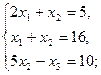
2.7. 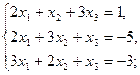 2.8.
2.8. 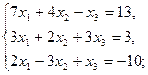
2.9. 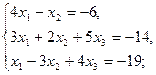 2.10.
2.10. 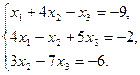
3. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 3/8 вклада, который составляет 800 ден. ед., вложили в первый банк, 1/8 вклада вложили во второй банк и оставшуюся часть вклада - в третий банк. К концу года сумма этих вкладов стала равна 907 ден. ед. Если бы первоначально 1/8 вклада положили в первый банк, 4/8 вклада - во второй банк, оставшуюся часть вклада - в третий банк, то к концу года сумма этих вкладов стала бы равна 894 ден. ед.. Если бы 4/8 вклада вложили в первый банк, 3/8 вклада - во второй банк, оставшуюся часть вклада - в третий банк, то к концу года сумма этих вкладов была бы равна 903 ден. ед.
а) Записать в математической форме условия вложения денег.
б) Определить, какой процент начисляет каждый банк?
4. В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл.ден.ед.
|
отрасль | потребление | конечный продукт | ||
| промышленность | сельское хозяйство | |||
| производство | промышленность сельское хозяйство | 0,3 0,15 | 0,2 0,1 | 300 100 |
Найти плановые объемы валовой продукции отраслей, межотраслевые поставки, чистую продукцию.
5.4. Домашнее задание
1. Проверить совместность систем уравнений (по теореме Кронекера–Капелли):
1.1. 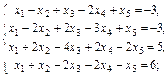 1.2.
1.2. 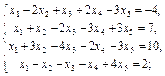
1.3. 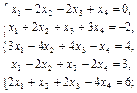 1.4.
1.4. 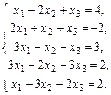
2. Решить системы линейных уравнений:
а) методом обратной матрицы;
б) по формуле Крамера.
2.1. 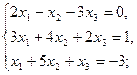 2.2.
2.2. 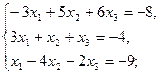
2.3. 
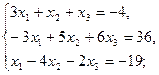 2.4.
2.4. 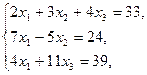
2.5. 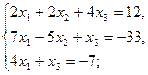 2.6.
2.6. 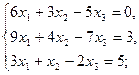
2.7. 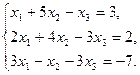
3. Инкассатор привез в поликлинику зарплату в объеме 270 купюр по 50 тыс. рублей, 95 купюр по 10 тыс. рублей и 155 тысячерублевых купюр. Размер выдаваемой зарплаты составил у каждого врача 522 тыс. руб., 315 тыс. руб. у каждой медсестры и 233 тыс. руб. - у младшего медперсонала.
а) Записать в математической форме условия выдачи зарплаты.
б) Сколько врачей, медсестер и младшего медперсонала было в поликлинике, если каждому работнику зарплата выдавалась минимальным числом купюр?
4. Дан следующий баланс «затраты - выпуск» продукции по двум отраслям (отрасль I - сталелитейная промышленность, отрасль II - энергетика)
| I | II | Потребление | Валовый выпуск | |
| I | 5 | 20 | 75 | 100 |
| II | 15 | 5 | 30 | 50 |
Построить структурную матрицу и рассчитать валовой выпуск на новый вариант потребления: Д = (150, 30).
Дата: 2019-02-02, просмотров: 448.