Задачник-практикум
По линейной алгебре
Часть I .
Курск, 2018
Задачник-практикум рассмотрен и утвержден на заседании кафедры «Алгебры, геометрии и ТОМ» «17» мая 2018 г., протокол № 10
Авторы: к.ф.м.н., доцент Толстова Г.С., к.т.н.,
доцент Бурилич И.Н., ст.преподаватель Бочарова О.Е.
Задачник-практикум по линейной алгебре, часть I : учебное пособие для студентов – Курск: 2018. – 68с.
Содержание.
Тема 1. Матрицы. Операции над матрицами. 4
1.1. Краткие теоретические сведения. 4
1.2. Пример выполнения заданий практической части. 9
1.3. Задания для аудиторного занятия. 13
1.4. Домашнее задание. 14
Тема 2. Определители n-го порядка. Методы вычисления. 16
2.1. Краткие теоретические сведения. 16
2.2 . Пример выполнения заданий практической части. 19
2.3. Задания для аудиторного занятия. 25
2.4. Домашнее задание. 26
Тема 3. Нахождение обратных матриц. Решение матричных уравнений. 27
3.1. Краткие теоретические сведения. 27
3.2. Пример выполнения заданий практической части. 29
3.3. Задания для аудиторного занятия. 36
3.4. Домашнее задание. 37
Тема 4. Ранг матрицы.. 38
4.1. Краткие теоретические сведения. 38
4.2. Пример выполнения заданий практической части. 40
4.3. Задания для аудиторного занятия. 43
4.4. Домашнее задание. 44
Тема 5. Решение систем линейных уравнений: матричный способ, формулы Крамера. Теорема Кронекера-Капелли: исследование числа решений систем 45
5.1. Краткие теоретические сведения. 45
5.2. Пример выполнения заданий практической части. 48
5.3. Задания для аудиторного занятия. 53
5.4. Домашнее задание. 55
Тема 6. Решение систем линейных уравнений методом Гаусса. 57
Фундаментальная система решений. 57
6.1. Краткие теоретические сведения. 57
6.2. Пример выполнения заданий практической части. 60
6.3. Задания для аудиторного занятия. 65
6.4. Домашнее задание. 67
Тема 1. Матрицы. Операции над матрицами
Пример выполнения заданий практической части
Пример 1. Даны матрицы 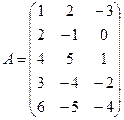 ;
; 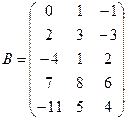 ;
; 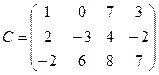 . Найти сумму А+В и произведение А´С.
. Найти сумму А+В и произведение А´С.
Решение.
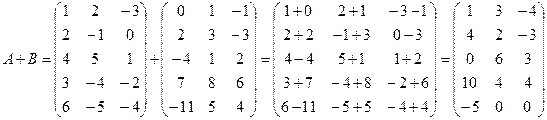 .
.
Пусть А´С=D. Тогда
d11=1×1+2×2+(-3) ×(-2)=11
d12=1×0+2×(-3)+(-3) ×6=-24
d13=1×7+2×4+(-3) ×8=-9
d14=1×3+2×(-2)+(-3) ×7=-22
d21=2×1+(-1) ×2+0×(-2)=0
d22=2×0+(-1) ×(-3)+0×6=3
d23=2×7+(-1) ×4+0×8=10
d24=2×3+(-1) ×(-2)+0×7=8
d31=4×1+5×2+1×(-2)=12
d32=4×0+5×(-3)+1×6=-9
d33=4×7+5×4+1×8=56
d34=4×3+5×(-2)+1×7=9
d41=3×1+(-4) ×2+(-2) ×(-2)=-1
d42=3×0+(-4) ×(-3)+(-2) ×6=0
d43=3×7+(-4) ×4+(-2) ×8=-11
d44=3×3+(-4) ×(-2)+(-2) ×7=3
d51=6×1+(-5) ×2+(-4) ×(-2)=4
d52=6×0+(-5) ×(-3)+(-4) ×6=-9
d53=6×7+(-5) ×4+(-4) ×8=-10
d54=6×3+(-5) ×(-2)+(-4) ×7=0.
Таким образом, 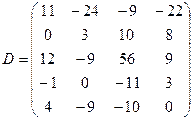 .
.
Пример 2. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если 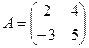 ,
, 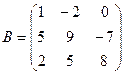 ,
, 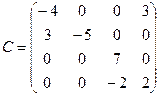 .
.
Решение.
- Найдем значение многочлена от матрицы А.
1) 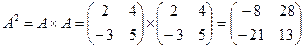 ;
;
2)  ;
;
3) 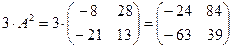 ;
;
4) 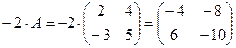 ;
;
5) 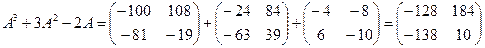 .
.
2. Найдем значение многочлена от матрицы В.
1) 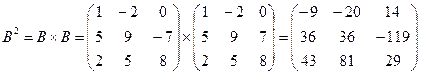 ;
;
2)  ;
;
3) 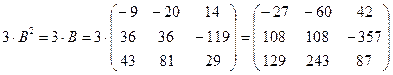 ;
;
4)  ;
;
5) 
3. Найдем значение многочлена от матрицы С.
1) 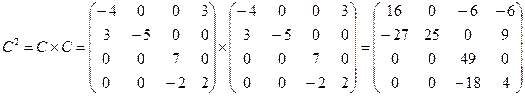 ;
;
2) 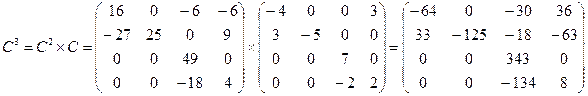 ;
;
3) 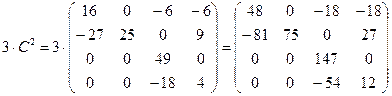 ;
;
4) 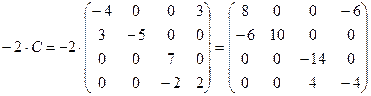
5) 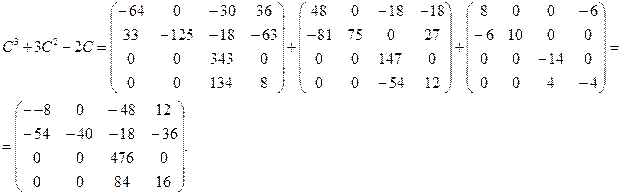
Ответ: 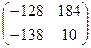 ;
; 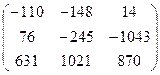 ;
; 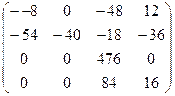 .
.
Пример 3. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70 ден. ед., а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
| 1 | 20 | 35 | 10 |
| 2 | 15 | 27 | 8 |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
 ,
, 
Тогда матрица затрат на перевозки будет иметь вид 
 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Задания для аудиторного занятия
1. Найти матрицу 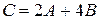 , если
, если 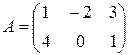 ,
, 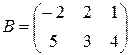 .
.
2.Заданы матрицы А, В, С. Найти произведения А´В, В´С, А´С, А´В´С.
2.1 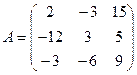 ,
, 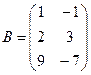 ,
, 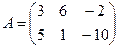 ;
;
2.2. 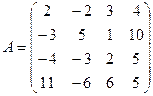 ,
, 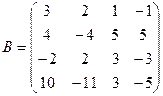 ,
, 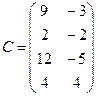 .
.
3. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если  ,
, 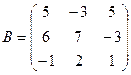 ,
, 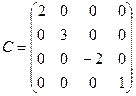 .
.
4. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей-строкой X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица-строка С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица-строка P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
Сколько метров ткани каждого типа потребуется для выполнения плана?
1.4. Домашнее задание
1. Найти матрицу Х если:
1.1. 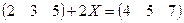 ;
;
1.2. 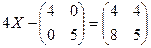 .
. 
2. Найти произведения матриц:
2.1. 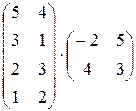 ; 2.2.
; 2.2. 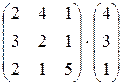 ;
;
2.3. 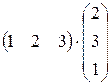 .
.
3. Вычислить 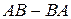 , если
, если 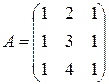 ,
, 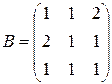 .
.
4. Найти значение многочлена f(x)=ху2+3х2 у-2ух от матриц Х, У, если
4.1. 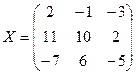 ,
, 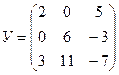 ;
;
4.2. 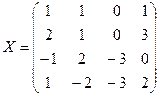 ,
, 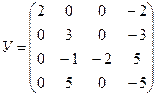 .
.
5. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей (вектором) X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица (вектор) С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица (вектор) P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
5.1. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
5.2. Определить стоимость всей ткани, необходимой для выполнения плана.
5.3. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Определителей n -го порядка
Пример выполнения заданий практической части
Пример 1. Найти значение определителя, пользуясь правилом треугольника: 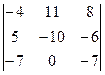 .
.
Решение.
Для вычисления значения определителя воспользуемся формулой 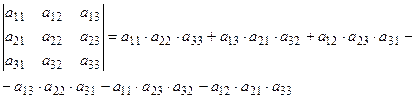 .
.
Получаем:
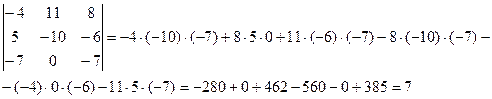
Пример 2. Найти значение определителя методом приведения к треугольному виду: 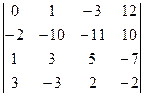 .
.
Решение.
Для приведения определителя к треугольному виду воспользуемся элементарными преобразованиями.
Сначала получим а11=1.
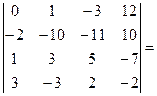 [поменяем местами первый и второй столбец, поменяв при этом знак перед определителем]= –
[поменяем местами первый и второй столбец, поменяв при этом знак перед определителем]= – 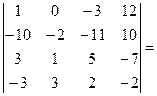 [будем получать нули в первом столбце; умножим первую строку на 10 и сложим со второй] =
[будем получать нули в первом столбце; умножим первую строку на 10 и сложим со второй] =
= – 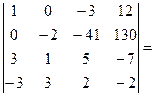 [умножим первую строку на 3 и вычтем из третьей] =
[умножим первую строку на 3 и вычтем из третьей] =
= - 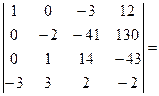 [умножим первую строку на 3 и сложим с четвертой]=
[умножим первую строку на 3 и сложим с четвертой]=
= – 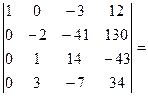 [поменяем местами вторую и третью строки, поменяв знак перед определителем]=
[поменяем местами вторую и третью строки, поменяв знак перед определителем]= 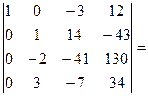 [ будем получать нули во втором столбце; умножим вторую строку на 2 и сложим с третьей]=
[ будем получать нули во втором столбце; умножим вторую строку на 2 и сложим с третьей]= 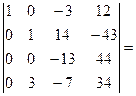 [умножим вторую строку
[умножим вторую строку
на 3 и вычтем из четвертой]= 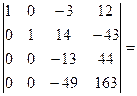 [умножим третью строку на 4 и вычтем из четвертой] =
[умножим третью строку на 4 и вычтем из четвертой] = 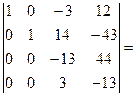 [умножим четвертую строку на 4 сложим с третьей]=
[умножим четвертую строку на 4 сложим с третьей]= 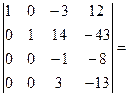 [умножим третью строку на 3 и сложим с четвертой]= =
[умножим третью строку на 3 и сложим с четвертой]= = 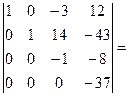 [определитель приведен к треугольному виду; найдем произведение элементов главной диагонали]=37.
[определитель приведен к треугольному виду; найдем произведение элементов главной диагонали]=37.
Пример 3. Найти значение определителя, разложив его по элементам первой и третьей строки: 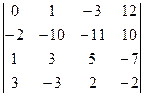 .
.
Решение.
Для вычисления значения определителя, воспользуемся теоремой Лапласа. Так как указано две строки, а данный определитель четвертого порядка, то и миноры, и их алгебраические дополнения будут являться определителями второго порядка. Получаем:
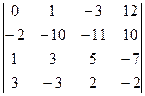 =
= 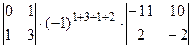 +
+ 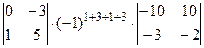 +
+
+ 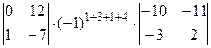 +
+ 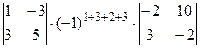 +
+
+ 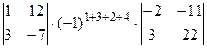 +
+ 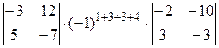 = (0×3-1×1) ×(-1)7×(-11×(-2)-10×2)+(0×5-(-3) ×1) ×(-1)8×(-10×(-2)-10×(-3))+(0×(-7)-12×1) ×(-1)9(-10×2-(-11) ×(-3))+(1×5-(-3) ×3)
= (0×3-1×1) ×(-1)7×(-11×(-2)-10×2)+(0×5-(-3) ×1) ×(-1)8×(-10×(-2)-10×(-3))+(0×(-7)-12×1) ×(-1)9(-10×2-(-11) ×(-3))+(1×5-(-3) ×3)
×(-1)9×(-2×(-2)-10×3)+(1×(-7)-13×3) ×(-1)10×(-2×2-(-11) ×3)+(-3×(-7)-12×5) ×(-1)11(-2×(-3)-(-10) ×3) = (-1)×(-1) ×2+3×50+(-12) ×(-1) ×(-53)+14×(-1) ×(-26)+(-43) ×29+(-39) ×(-1) ×36=37.
Пример 4. Найти значение определителя методом понижения порядка: 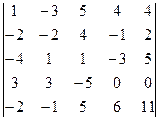 .
.
Решение.
Для того чтобы воспользоваться следствием теоремы Лапласа, получим нули, например, в первом столбце.
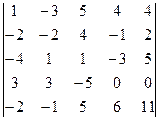 =[умножим первую строку на 2 и сложим со второй]= =
=[умножим первую строку на 2 и сложим со второй]= = 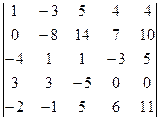 =[умножим первую строку на 4 и сложим с третьей]= =
=[умножим первую строку на 4 и сложим с третьей]= = 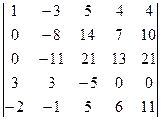 =[умножим первую строку на 3 и вычтем из четвертой]= =
=[умножим первую строку на 3 и вычтем из четвертой]= = 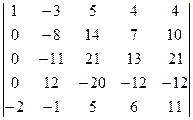 =[умножим первую строку на 2 и сложим с пятой]=
=[умножим первую строку на 2 и сложим с пятой]=
= 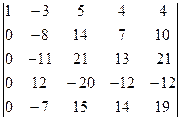 =[разложим определитель по элементам первого столбца, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
=[разложим определитель по элементам первого столбца, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]= 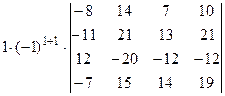 =[вынесем за знак определителя из третьей строки множитель (-4)]=
=[вынесем за знак определителя из третьей строки множитель (-4)]= 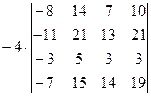 =[вынесем за знак определителя из первого столбца множитель (-1)]=
=[вынесем за знак определителя из первого столбца множитель (-1)]= 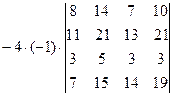 =[вычтем из первой строки четвертую, чтобы получить единицу в первой строке]=
=[вычтем из первой строки четвертую, чтобы получить единицу в первой строке]= 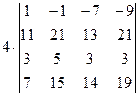 =[в данном случае удобнее получать нули в первой строке, поэтому сложим первый столбец со вторым]= =
=[в данном случае удобнее получать нули в первой строке, поэтому сложим первый столбец со вторым]= = 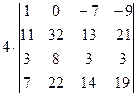 =[умножим первый столбец на 7 и сложим с третьим]= =
=[умножим первый столбец на 7 и сложим с третьим]= = 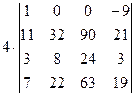 =[ умножим первый столбец на 9 и сложим с четвертым]= =
=[ умножим первый столбец на 9 и сложим с четвертым]= = 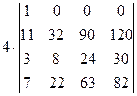 =[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=
= 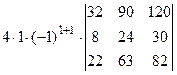 =
= 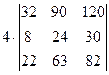 =[вынесем из первой строки множитель 2]= =
=[вынесем из первой строки множитель 2]= = 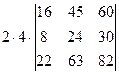 =
= 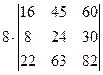 =[вынесем из второй строки множитель 2]=
=[вынесем из второй строки множитель 2]= 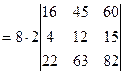 =[вынесем из первого столбца множитель 2]= =
=[вынесем из первого столбца множитель 2]= = 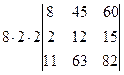 =
= 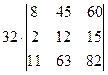 =[вынесем из второго столбца множитель 3]= =
=[вынесем из второго столбца множитель 3]= = 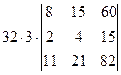 =[вторую строку умножим на 4 и вычтем из первой]= =
=[вторую строку умножим на 4 и вычтем из первой]= = 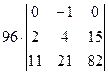 =[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме второго, будут равны нулю]=
=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме второго, будут равны нулю]= 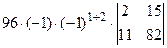 =96×(2×82-11×15)=-96.
=96×(2×82-11×15)=-96.
Задания для аудиторного занятия
1. Вычислить определители с помощью правила треугольников:
1.1. 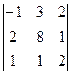 ; 1.2.
; 1.2. 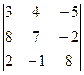 ..
.. 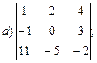
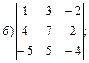
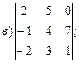 1.2
1.2 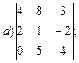
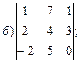
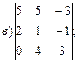
2. Решить уравнения:
2.1. 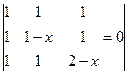 ; 2.2.
; 2.2. 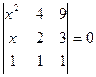 .
.
3. Вычислить определитель, разложив его по элементам:
3.1. 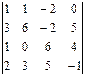 4-го столбца; 3.2.
4-го столбца; 3.2. 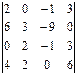 3-ей строки.
3-ей строки.
4. Вычислить определители методом приведения к треугольному виду:
4.1. 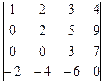 ; 4.2.
; 4.2. 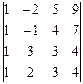 .
.
5. Вычислить определители:
5.1. 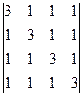 ; 5.2.
; 5.2. 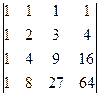
5.3. 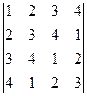 .
. 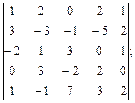 4.2.
4.2. 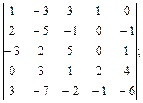 4.3.
4.3. 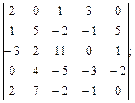
4.4. 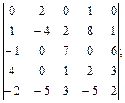 4.5.
4.5. 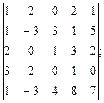 4.6.
4.6. 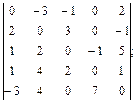
4.7. 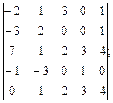 4.8.
4.8. 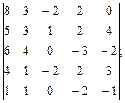 4.9.
4.9. 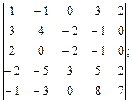
2.4. Домашнее задание
1. Вычислить определители с помощью правила треугольников:
1.1. 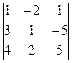 ; 1.2.
; 1.2. 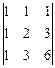 .
.
2. Вычислить определитель, разложив его по элементам:
2.1. 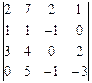 4-ой строки; 2.2.
4-ой строки; 2.2. 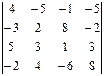 3-его столбца.
3-его столбца.
3. Вычислить определители:
3.1. 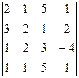 ; 3.2.
; 3.2. 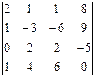 ;
;
3.3. 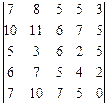
Матричные уравнения.
Определение. Матричным уравнением будем называть уравнение вида A´X=B, где А и В заданные матрицы, Х – неизвестная матрица.
Если матрица А невырожденная, тогда для нее существует обратная. Умножив обе части уравнения A´X=B на А-1, получим
A-1 ´ (A´X)=A-1 ´BÞ (A-1 ´A)´C=A-1 ´B Þ C=A-1 ´B
Покажем, что Х - решение уравнения A´X=B:
A´ (A-1´B)= (A´A-1) ´B=Е´В=В Û B=B.
Пример выполнения заданий практической части
Пример 1. Найти матрицу А-1, обратную матрице 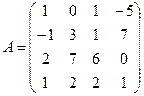 .
.
Решение.
1. Определитель матрицы А : 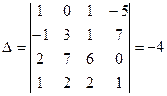 .
.
2. Найдем алгебраические дополнения ко всем элементам матрицы:
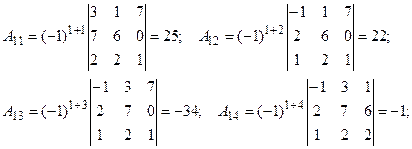
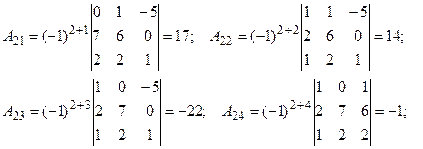
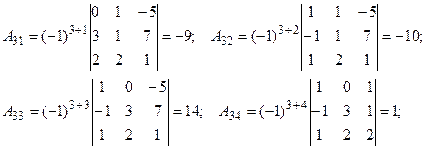
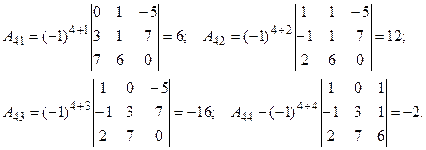
3. Составим матрицу, заменив все элементы матрицы А их алгебраическими дополнениями:
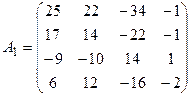 .
.
4. Транспонируем полученную матрицу А1: 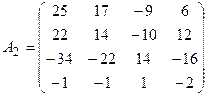 .
.
5. Разделим все элементы матрицы А2 на значение определителя D=-4: 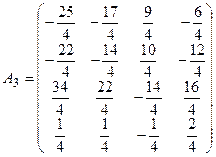 .
.
Таким образом, матрица, обратная матрице 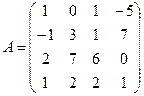 , имеет вид:
, имеет вид: 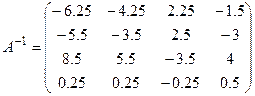 .
.
Пример 2. Найти матрицу А-1, обратную матрице 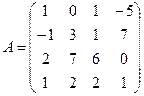 .
.
Решение.
1. Единичная матрица четвертого порядка имеет вид: 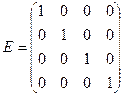 . Составим матрицу (А|Е):
. Составим матрицу (А|Е): 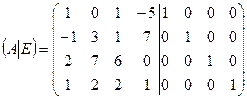 .
.
2. С помощью элементарных преобразований получим слева от вертикальной черты единичную матрицу Е.
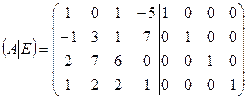 =[ко второй строке прибавим первую]= =
=[ко второй строке прибавим первую]= = 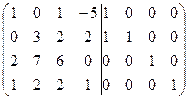 =[вычтем из третьей строки первую, умноженную на 2]= =
=[вычтем из третьей строки первую, умноженную на 2]= = 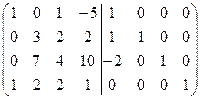 =[вычтем из четвертой строки первую]= =
=[вычтем из четвертой строки первую]= = 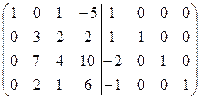 =[вычтем из второй строки четвертую, для того чтобы получить во второй строке второй элемент равный 1]= =
=[вычтем из второй строки четвертую, для того чтобы получить во второй строке второй элемент равный 1]= = 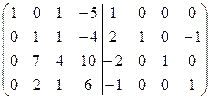 =[вычтем из третьей строки вторую, умноженную на 7]= =
=[вычтем из третьей строки вторую, умноженную на 7]= = 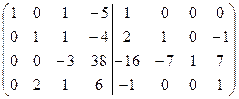 =[вычтем из четвертой строки вторую, умноженную на 2]=
=[вычтем из четвертой строки вторую, умноженную на 2]= 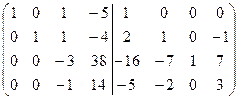 =[вычтем из третьей строки четвертую, умноженную на 2]=
=[вычтем из третьей строки четвертую, умноженную на 2]= 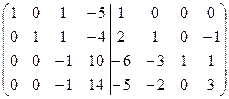 =[разделим все элементы третьей строки на (-1)]=
=[разделим все элементы третьей строки на (-1)]= 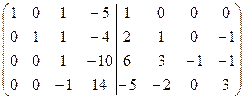 =[прибавим к четвертой строке третью]= =
=[прибавим к четвертой строке третью]= = 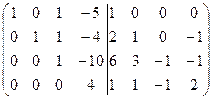 =[разделим все элементы четвертой строки
=[разделим все элементы четвертой строки
на 4]= 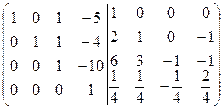 =[к третьей строке прибавим четвертую, умноженную на 10]=
=[к третьей строке прибавим четвертую, умноженную на 10]= 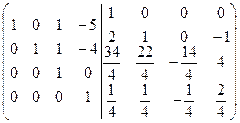 =[ко второй строке прибавим четвертую, умноженную на 4]=
=[ко второй строке прибавим четвертую, умноженную на 4]= 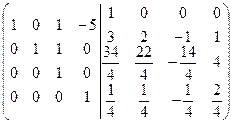 =[к первой строке прибавим четвертую, умноженную на 5]=
=[к первой строке прибавим четвертую, умноженную на 5]= 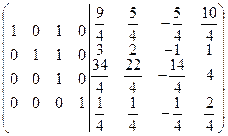 =[из второй строки вычтем третью] =
=[из второй строки вычтем третью] = 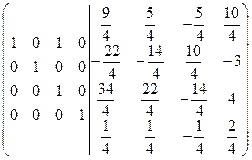 =[из первой строки вычтем третью]= =
=[из первой строки вычтем третью]= = 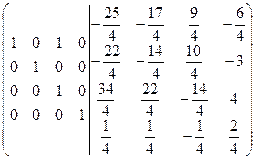 .
.
Таким образом, матрица, обратная матрице А, имеет вид:  или
или 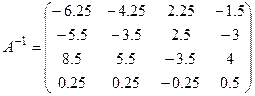 .
.
Пример 3. Решить матричные уравнения A´X=B, A´X´В=С, если
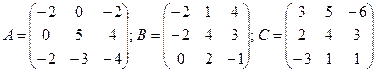
Решение.
1. Решим матричное уравнение 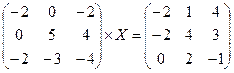 .
.
C=A-1 ´B
1) Найдем матрицу А-1. Воспользуемся первым способом.
DА=-4.
2) 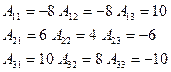
3) Составим матрицу из алгебраических дополнений к элементам матрицы А:
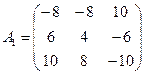
4) Транспонируем полученную матрицу: 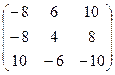
5) Разделим каждый элемент полученной матрицы на значение DА= - 4: 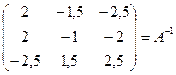
6) 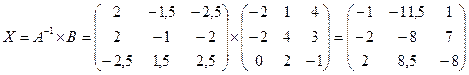
2. Решим матричное уравнение 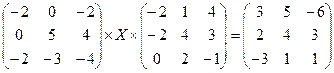 .
.
1) 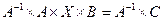 ;
;
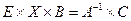 ;
;
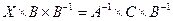 ;
;
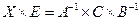 ;
;
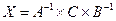 .
.
2) Найдем матрицу, обратную к матрице В:
DВ=2
3) 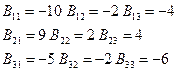
4) Составим матрицу из алгебраических дополнений к элементам матрицы В:
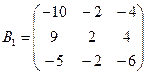
5) Транспонируем полученную матрицу: 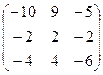
6) Разделим каждый элемент полученной матрицы на значение DВ=2: 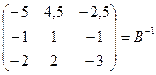
7)
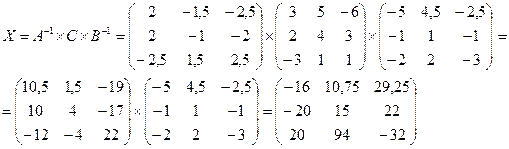
Ответ: 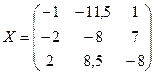 ;
; 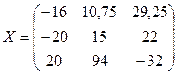 .
.
Задания для аудиторного занятия
- Убедиться, что каждая из следующих матриц обратима и найти к каждой матрице обратную:
1.1. 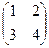 ; 1.2.
; 1.2. 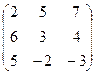 ; 1.3.
; 1.3. 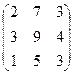 ;
;
1.4.  ; 1.5.
; 1.5. 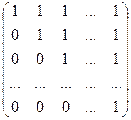 ..1
..1 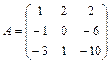 ;
; 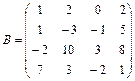 ; 3.2
; 3.2 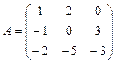 ;
; 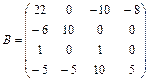 ;
;
3.3 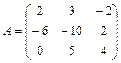 ;
; 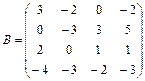 ; 3.4
; 3.4 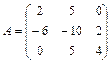 ;
; 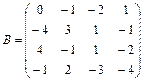 ;
;
3.5 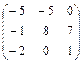 ;
; 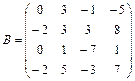 ; 3.6
; 3.6 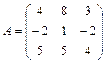 ;
; 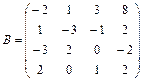 ;
;
2. Решить матричные уравнения 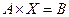 и
и 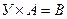 , если:
, если:
2.1. 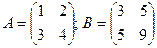 ;
;
2.2. 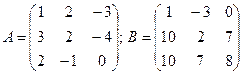 ;
;
2.3. 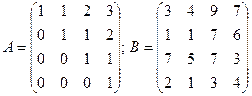 .
.
3. Решить матричные уравнения:
3.1. 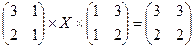 ; 3.2.
; 3.2. 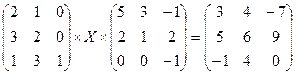 ;
;
3.3. 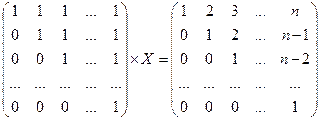 .
.
4. Пусть А и В – обратимые матрицы одного и того же порядка. Показать, что следующие равенства равносильны между собой:
€ 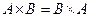 ;
;
€ 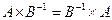 ;
;
€ 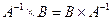 ;
;
€ 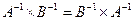 .
.
3.4. Домашнее задание
- Для каждой матрицы найти обратную.
1.1. 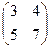 ; 1.2.
; 1.2. 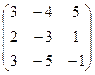 ; 1.3.
; 1.3. 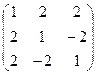 ;
;
1.4. 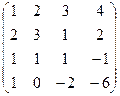 ; 1.5.
; 1.5. 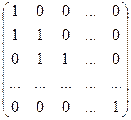 .
.
2. Решить матричные уравнения 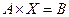 и
и 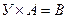 , если:
, если:
2.1. 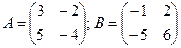 ; 2.2.
; 2.2. 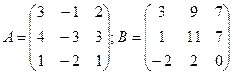 .
.
3. Решить матричные уравнения:
3.1. 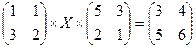 ;
;
3.2. 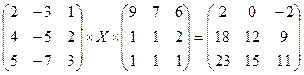 ;
;
3.3. 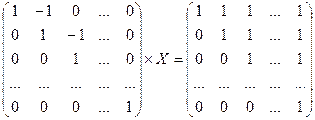 .
.
4. Определить, как изменится обратная матрица А-1, если в данной матрице А:
4.1. переставить i-ую и g-ую строки;
4.2. все элементы i-ой строки умножить на число к¹0;
4.3. к i-ой строке прибавить g-ую строку, умноженную на число к¹0.
Тема 4. Ранг матрицы
Пример выполнения заданий практической части
Пример 1. Найти методом окаймления миноров ранг матрицы
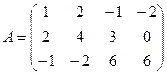 .
.
Решение . Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
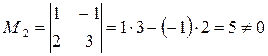 .
.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
добавить второй столбец или четвертый). Вычисляем их:
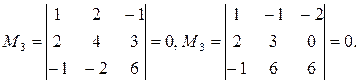
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум: 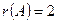 .
.
Пример 2. Найти ранг матрицы с помощью элементарных преобразований:
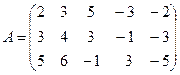 .
.
Решение . Из второй строки вычтем первую и переставим эти строки
 .
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
 ;
;
из третьей строки вычтем первую, получим матрицу
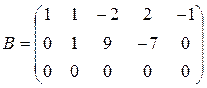 ,
,
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2.
Пример 3. Выяснить, при каком значении параметра 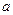 матрица имеет 3 линейно независимые строки:
матрица имеет 3 линейно независимые строки:  .
.
Решение. Матрица 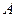 имеет три линейно независимые строки, если ее ранг равен 3, т.е.
имеет три линейно независимые строки, если ее ранг равен 3, т.е. 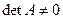 . Вычислим определитель матрицы:
. Вычислим определитель матрицы:
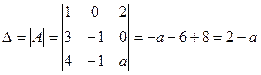 ,
,
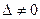 , т.е.
, т.е. 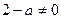 ;
; 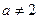 .
.
Следовательно, при всех значениях 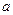 , кроме
, кроме  , все строки линейно независимы.
, все строки линейно независимы.
Пример 4. Определить максимальное число линейно независимых строк (столбцов) матрицы: 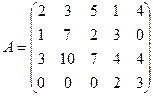 .
.
Решение. С помощью элементарных преобразований, не меняющих ранга матрицы, приведем ее к ступенчатому виду:
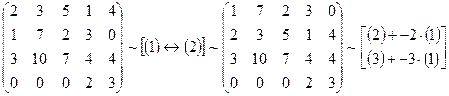 ~
~ 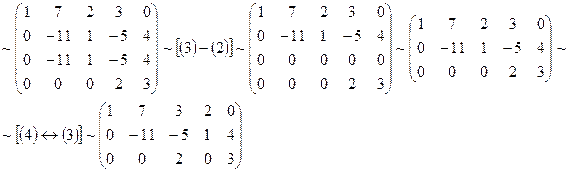
Значит, ранг матрицы 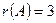 и исходная матрица имеет 3 линейно независимые строки (или столбца).
и исходная матрица имеет 3 линейно независимые строки (или столбца).
Задания для аудиторного занятия
1. Найти методом окаймления миноров ранг матрицы:
1.1.  ; 1.2.
; 1.2. 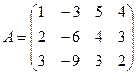 ;
;
1.3. 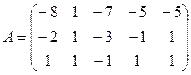 ; 1.4.
; 1.4. 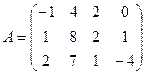 .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1. 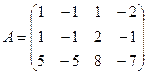 ; 2.2.
; 2.2. 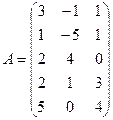 ;
;
2.3. 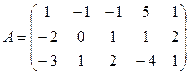 ; 2.4.
; 2.4. 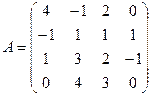 ;
;
2.5. 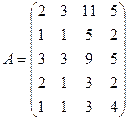 ; 2.6.
; 2.6. 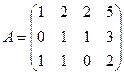 .
.
3. Найти максимальное число линейно независимых строк матриц:
3.1. 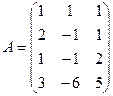 ; 3.2.
; 3.2. 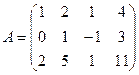 ;
;
3.3. 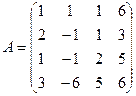 ; 3.4.
; 3.4. 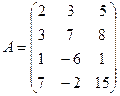 .
.
4.4. Домашнее задание
1. Найти методом окаймления миноров ранг матрицы:
1.1. 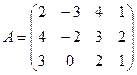 ; 1.2.
; 1.2. 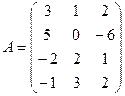 ;
;
1.3.  .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1.  ; 2.2.
; 2.2. 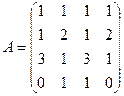 ;
;
2.3.  .
.
3. Найти максимальное число линейно независимых столбцов матриц:
3.1. 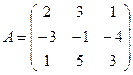 ; 3.2.
; 3.2. 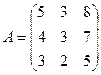 .
.
Пример выполнения заданий практической части
Пример 1. Исследовать систему уравнений на совместность:
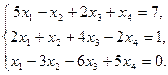
Решение. Выписываем расширенную матрицу системы:
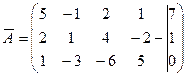
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу
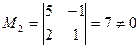
содержащие его миноры третьего порядка равны нулю:
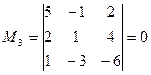 ;
; 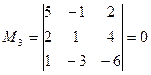
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы 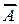 рассмотрим окаймляющий минор
рассмотрим окаймляющий минор
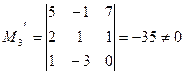
Значит, ранг расширенной матрицы r( 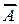 ) = 3. Поскольку r(A) ≠ r(
) = 3. Поскольку r(A) ≠ r( 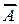 ), то система несовместна.
), то система несовместна.
Пример 2. Решить систему матричным способом: 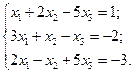
Решение .
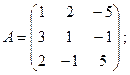
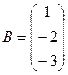 .
.
А×Х = В; Х = А-1 × В.
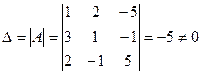 .
.
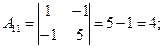
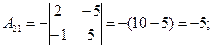
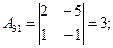
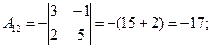
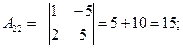
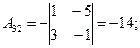
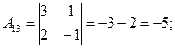
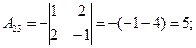
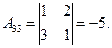
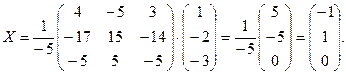
Пример 3. Решить систему уравнений, воспользовавшись формулами Крамера (4.4):
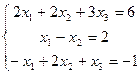
Решение.
1) Определитель данной системы 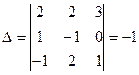 .
.
2) Найдем определитель 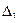 , заменив в определителе D первый столбец, столбцом свободных членов:
, заменив в определителе D первый столбец, столбцом свободных членов: 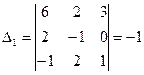 .
.
3) Найдем определитель 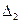 , заменив в определителе D второй столбец, столбцом свободных членов:
, заменив в определителе D второй столбец, столбцом свободных членов: 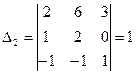 .
.
4) Найдем определитель 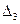 , заменив в определителе D третий столбец, столбцом свободных членов:
, заменив в определителе D третий столбец, столбцом свободных членов: 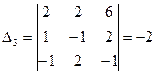 .
.
5) Найдем решения системы, воспользовавшись формулами Крамера (4.4):
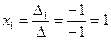 ;
; 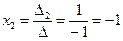 ;
; 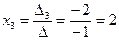 .
.
Ответ: (1, -1, 2).
Пример 4. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 1/3 вклада, который составляет 600 ден. ед., вложили в первый банк, а оставшуюся часть вклада во второй банк. К концу года сумма этих вкладов стала равна 700 ден. ед. Если бы первоначально 1/3 вклада положили во второй банк, а оставшуюся часть вклада - в первый банк, то к концу года сумма этих вкладов стала бы равна 680 ден. ед.
а) Записать в математической форме условия вложения денег.
б) Какой процент начисляет каждый банк?
Решение. Пусть x 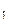 – процентная ставка начисления I-го банка, x
– процентная ставка начисления I-го банка, x 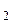 – процентная ставка начисления II-го банка. Тогда
– процентная ставка начисления II-го банка. Тогда
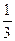 вклада в I банк составит:
вклада в I банк составит: 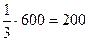 д.е.
д.е.
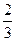 вклада в I банк составит:
вклада в I банк составит: 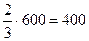 д.е.
д.е.
Так как к концу года суммы этих вкладов составили 700 д.е. в I-м банке и 680 д.е. во 2-м банке. Составим систему уравнений:
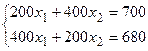 .
.
Решим систему по формулам Крамера:
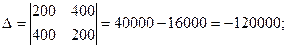
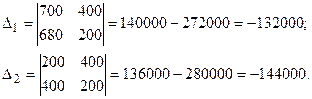
Тогда 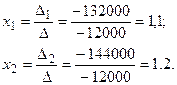
Таким образом, процентная ставка I-го банка составляет 10% и II-го банка 20%.
Пример 5. В таблице приведены данные об исполнении баланса за отчетный период.
|
отрасль | потребление | конечный продукт | валовый выпуск | ||
| энергетика | машино- строение | ||||
| производство | энергетика машиностроение | 7 12 | 21 15 | 72 123 | 100 150 |
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне.
Решение . По условию имеем матрицу-столбец конечного продукта

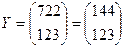
Валовый выпуск: x1=100; x2=150.
Объем продукции: x11=7; x12=21;
x21=12; x22=15.
По формуле 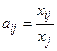 , находим
, находим
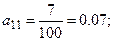
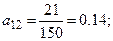
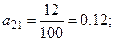
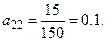
Т.е. матрица прямых затрат примет вид
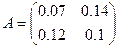 .
.
Полученная матрица имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
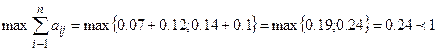 .
.
Необходимый объем валового выпуска X найдем по формуле: X = (E – A)-1Y.
Найдем матрицу полных затрат
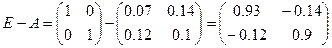
Т.к. 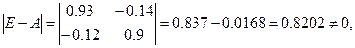
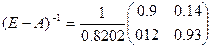 ,
,
тогда 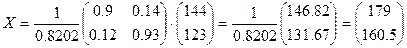 .
.
Т.е. валовый выпуск в энергетической отрасли надо увеличить до 179 усл.ед., а в машиностроительной – до 160.5 усл.ед..
Задания для аудиторного занятия
1. Проверить совместность систем уравнений (по теореме Кронекера–Капелли):
1.1. 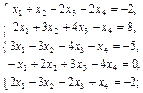 1.2.
1.2. 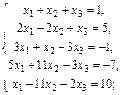
1.3. 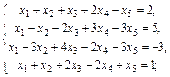 1.4.
1.4. 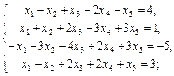
1.5. 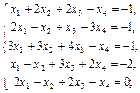 1.6.
1.6. 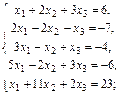
2. Решить системы линейных уравнений:
а) методом обратной матрицы;
б) по формуле Крамера.
2.1. 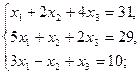 2.2.
2.2. 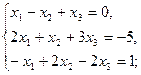
2.3. 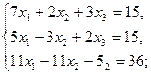 2.4.
2.4. 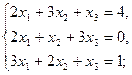
2.5. 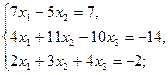 2.6.
2.6. 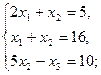
2.7. 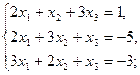 2.8.
2.8. 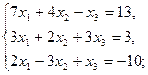
2.9. 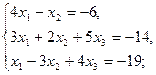 2.10.
2.10. 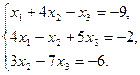
3. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 3/8 вклада, который составляет 800 ден. ед., вложили в первый банк, 1/8 вклада вложили во второй банк и оставшуюся часть вклада - в третий банк. К концу года сумма этих вкладов стала равна 907 ден. ед. Если бы первоначально 1/8 вклада положили в первый банк, 4/8 вклада - во второй банк, оставшуюся часть вклада - в третий банк, то к концу года сумма этих вкладов стала бы равна 894 ден. ед.. Если бы 4/8 вклада вложили в первый банк, 3/8 вклада - во второй банк, оставшуюся часть вклада - в третий банк, то к концу года сумма этих вкладов была бы равна 903 ден. ед.
а) Записать в математической форме условия вложения денег.
б) Определить, какой процент начисляет каждый банк?
4. В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл.ден.ед.
|
отрасль | потребление | конечный продукт | ||
| промышленность | сельское хозяйство | |||
| производство | промышленность сельское хозяйство | 0,3 0,15 | 0,2 0,1 | 300 100 |
Найти плановые объемы валовой продукции отраслей, межотраслевые поставки, чистую продукцию.
5.4. Домашнее задание
1. Проверить совместность систем уравнений (по теореме Кронекера–Капелли):
1.1. 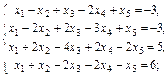 1.2.
1.2. 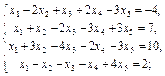
1.3. 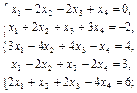 1.4.
1.4. 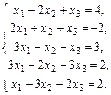
2. Решить системы линейных уравнений:
а) методом обратной матрицы;
б) по формуле Крамера.
2.1. 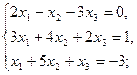 2.2.
2.2. 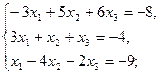
2.3. 
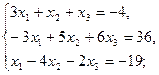 2.4.
2.4. 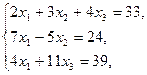
2.5. 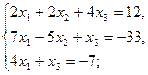 2.6.
2.6. 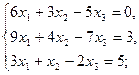
2.7. 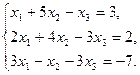
3. Инкассатор привез в поликлинику зарплату в объеме 270 купюр по 50 тыс. рублей, 95 купюр по 10 тыс. рублей и 155 тысячерублевых купюр. Размер выдаваемой зарплаты составил у каждого врача 522 тыс. руб., 315 тыс. руб. у каждой медсестры и 233 тыс. руб. - у младшего медперсонала.
а) Записать в математической форме условия выдачи зарплаты.
б) Сколько врачей, медсестер и младшего медперсонала было в поликлинике, если каждому работнику зарплата выдавалась минимальным числом купюр?
4. Дан следующий баланс «затраты - выпуск» продукции по двум отраслям (отрасль I - сталелитейная промышленность, отрасль II - энергетика)
| I | II | Потребление | Валовый выпуск | |
| I | 5 | 20 | 75 | 100 |
| II | 15 | 5 | 30 | 50 |
Построить структурную матрицу и рассчитать валовой выпуск на новый вариант потребления: Д = (150, 30).
Пример выполнения заданий практической части
Пример 1. Решить систему линейных уравнений
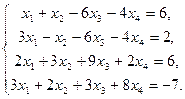
Решение. Выпишем расширенную матрицу системы и приведем ее к диагональному виду
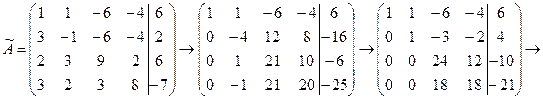

Таким образом, получили следующее решение системы линейных уравнений
х1=0, х2=2, х3=1/3, х4=-1,5.
Пример 2. Решить систему линейных уравнений
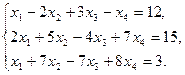
Решение. Составим расширенную матрицу системы и приведем ее к диагональному виду
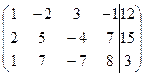 ~
~  ~
~ 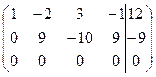
Матрица приведена к диагональному виду, запишем соответствующую систему линейных уравнений
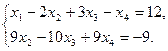
Данная система имеет бесконечно много решений. Чтобы найти общее решение переменные х3 и х4 объявим свободными, а остальные выразим через свободные, получим
 следовательно
следовательно
x3=c1, x4=c2, x2= 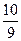 c1-c2-
c1-c2-  , x1=
, x1= 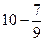 с1-с2
с1-с2
Таким образом, общее решение системы имеет вид:
( 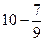 с1-с2,
с1-с2,  c1-c2-
c1-c2-  , с1, с2), где с1 и с2 – произвольные действительные числа. Если дать свободным переменным некоторые значения, получим частные решения системы.
, с1, с2), где с1 и с2 – произвольные действительные числа. Если дать свободным переменным некоторые значения, получим частные решения системы.
Пример 3. Решить систему уравнений
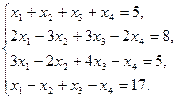 (*)
(*)
Решение. Составим расширенную матрицу системы и приведем ее к диагональному виду
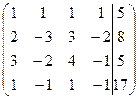 ~
~ 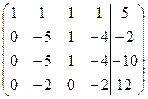 ~
~ 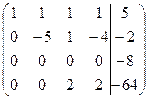
Третья строка соответствует уравнению
0x1+0x2+0x3+0x4=-8, которое не имеет решений, следовательно, система (*) также не имеет решений.
Пример 4. Решить систему линейных однородных уравнений
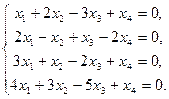 (
( 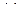 )
)
Решение. Будем решать систему методом Гаусса. Выпишем расширенную матрицу системы и упростим ее.
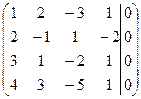 ~
~ 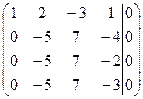 ~
~ 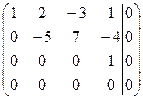 ~
~ 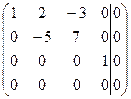
Получили систему, равносильную данной
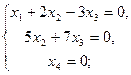 Û
Û 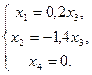 .
.
Система линейных уравнений имеет бесчисленное множество решений. Общее решение имеет вид (0,2с; -1,4с; с; 0).
Пример 5. Решить систему линейных однородных уравнений
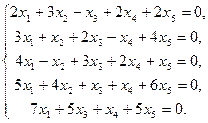
Решение. Будем решать систему методом Гаусса. Выпишем расширенную матрицу системы и упростим ее.
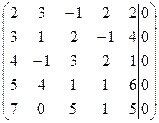 ~
~ 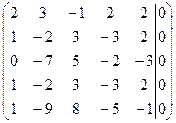 ~
~ 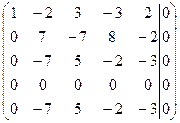 ~
~
~ 
Получили систему, равносильную данной
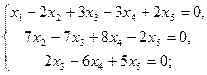 Û
Û 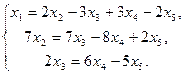
Переменные х4 и х5 объявляем свободными. Пусть х4=с1, х5=с2, тогда
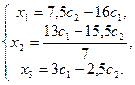
Общее решение системы имеет вид
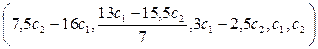
Пример 6. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
| Тип | Способ раскроя | ||
| заготовки | 1 | 2 | 3 |
| А | 3 | 2 | 1 |
| Б | 1 | 6 | 2 |
| В | 4 | 1 | 5 |
Записать в математической форме условия выполнения задания.
Решение. Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3x заготовок типа А, при втором - 2y, при третьем - z. Для полного выполнения задания по заготовкам типа А сумма 3x +2y +z должна равняться 360, т.е.
3x +2y + z =360.
Аналогично получаем уравнения
x + 6y +2z = 300
4x + y + 5z = 675,
которым должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В. Решим систему методом Гаусса. Запишем расширенную матрицу системы и приведем ее с помощью элементарных преобразований к диагональному виду.
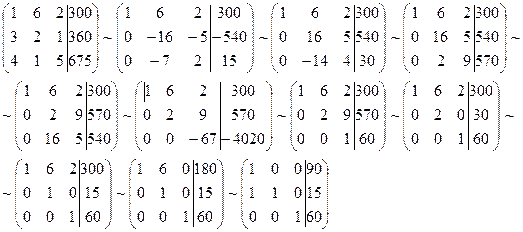
Следовательно, x = 90, y = 15, z = 60.
Задания для аудиторного занятия
1. Решить системы линейных уравнений:
1.1.  1.2.
1.2. 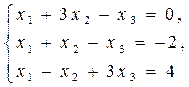
1.3. 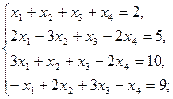 1.4.
1.4. 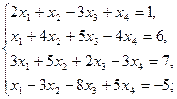
1.5.  1.6.
1.6. 
1.7. 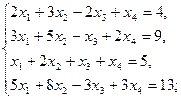 1.8.
1.8. 
1.9. 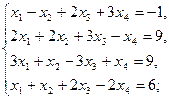 1.10.
1.10. 
1.11.  1.12.
1.12. 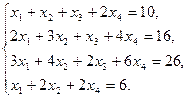
2. На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов. Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.
| Изделие | Выход из единицы сырья | |||
| способ | I | II | III | IV |
| А | 2 | 1 | 7 | 4 |
| Б | 6 | 12 | 2 | 3 |
3. Решить однородные системы линейных уравнений.
3.1. 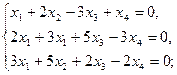 3.2.
3.2. 
3.3. 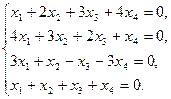
1.13
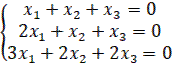
1.14 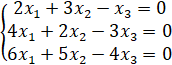
1.15 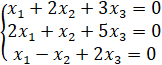
1.16 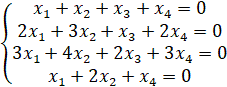
1.17 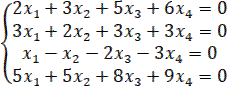
1.18 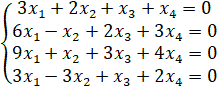
1.19 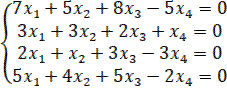
1.20 
1.21 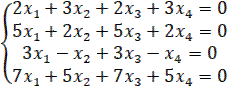
1.22 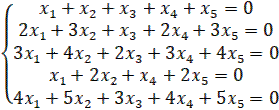
1.23 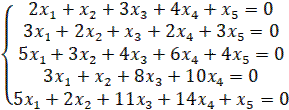
1.24 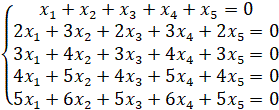
6.4. Домашнее задание
1. Решить системы линейных уравнений:
1.1.  1.2.
1.2. 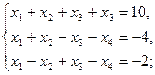
1.3. 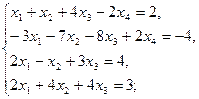 1.4.
1.4. 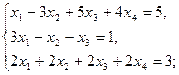
1.5. 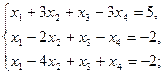 1.6.
1.6. 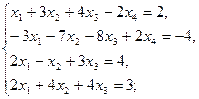
1.7. 
2. Решить однородные системы линейных уравнений.
2.1. 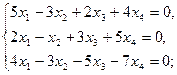 2.2.
2.2. 
2.3. 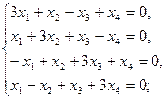 2.4.
2.4. 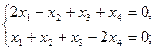
2.5. 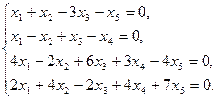
3. На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов. Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.
| Изделие | Выход из единицы сырья | |||
| способ | I | II | III | IV |
| А | 2 | 1 | 7 | 4 |
| Б | 6 | 12 | 2 | 3 |
Задачник-практикум
По линейной алгебре
Часть I .
Курск, 2018
Задачник-практикум рассмотрен и утвержден на заседании кафедры «Алгебры, геометрии и ТОМ» «17» мая 2018 г., протокол № 10
Авторы: к.ф.м.н., доцент Толстова Г.С., к.т.н.,
доцент Бурилич И.Н., ст.преподаватель Бочарова О.Е.
Задачник-практикум по линейной алгебре, часть I : учебное пособие для студентов – Курск: 2018. – 68с.
Содержание.
Тема 1. Матрицы. Операции над матрицами. 4
1.1. Краткие теоретические сведения. 4
1.2. Пример выполнения заданий практической части. 9
1.3. Задания для аудиторного занятия. 13
1.4. Домашнее задание. 14
Тема 2. Определители n-го порядка. Методы вычисления. 16
2.1. Краткие теоретические сведения. 16
2.2 . Пример выполнения заданий практической части. 19
2.3. Задания для аудиторного занятия. 25
2.4. Домашнее задание. 26
Тема 3. Нахождение обратных матриц. Решение матричных уравнений. 27
3.1. Краткие теоретические сведения. 27
3.2. Пример выполнения заданий практической части. 29
3.3. Задания для аудиторного занятия. 36
3.4. Домашнее задание. 37
Тема 4. Ранг матрицы.. 38
4.1. Краткие теоретические сведения. 38
4.2. Пример выполнения заданий практической части. 40
4.3. Задания для аудиторного занятия. 43
4.4. Домашнее задание. 44
Тема 5. Решение систем линейных уравнений: матричный способ, формулы Крамера. Теорема Кронекера-Капелли: исследование числа решений систем 45
5.1. Краткие теоретические сведения. 45
5.2. Пример выполнения заданий практической части. 48
5.3. Задания для аудиторного занятия. 53
5.4. Домашнее задание. 55
Тема 6. Решение систем линейных уравнений методом Гаусса. 57
Фундаментальная система решений. 57
6.1. Краткие теоретические сведения. 57
6.2. Пример выполнения заданий практической части. 60
6.3. Задания для аудиторного занятия. 65
6.4. Домашнее задание. 67
Тема 1. Матрицы. Операции над матрицами
Краткие теоретические сведения
Определение. Матрицей размера m ´ n называется прямоугольная таблица, состоящая из m строк и n столбцов, такая что на пересечении строки и столбца находится ровно одно число. Таблица, задающая матрицу, записывается в круглых скобках. Числа, из которых состоит матрица, называются элементами матрицы.
Например, 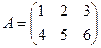 – матрица размера 2´3.
– матрица размера 2´3. 
Определение. Матрица размера 1´n называется матрица-строка; матрица размера m´1 называется матрица-столбец.
Например, А=(1 2 3 4 5 6) матрица-строка (размера 1´6), 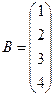 – матрица-столбец (размера 4´1).
– матрица-столбец (размера 4´1).
Определение. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, в противном случае (число строк не равно числу столбцов) прямоугольной.
Например, 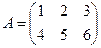 – прямоугольная матрица,
– прямоугольная матрица, 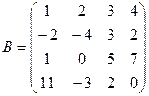 – квадратная матрица четвертого порядка (матрица размера 4´4).
– квадратная матрица четвертого порядка (матрица размера 4´4).
Определение. Элементы аij образуют главную диагональ (являются диагональными), если i=j, в противном случае элементы матрицы называют недиагональными.
Элементы аn1, an-1 2,…, a1n образуют побочную диагональ.
Определение. Квадратная матрица n-го порядка называется диагональной, если все недиагональные элементы равны 0.
То есть диагональная матрица имеет вид 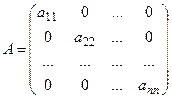 .
.
Например,  – диагональная матрица.
– диагональная матрица.
Определение. Диагональная матрица А, все диагональные элементы которой равны между собой, называется скалярной матрицей.
Например,  – скалярная матрица.
– скалярная матрица.
Определение. Скалярная матрица Е, все диагональные элементы которой равны единице, называется единичной матрицей. То есть, единичная матрица имеет вид 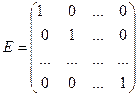 .
.
Например,  – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
Определение. Матрица О, все элементы которой равны 0, называется нулевой матрицей. То есть нулевая матрица имеет вид 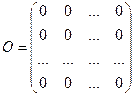 .
.
Определение. Транспонированием матрицы называется такое преобразование, при котором строки и столбцы меняются местами с сохранением их номеров. Полученная в результате такого преобразования матрица называется транспонированной по отношению к исходной и обозначается Аt
Например, 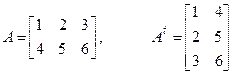 .
. 
Рассмотрим множество квадратных матриц
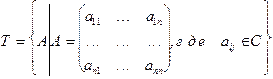
Определение. Под суммой квадратных матриц А и В будем понимать квадратную матрицу С, каждый элемент которой равен сумме соответствующих элементов матриц А и В.
"A,BÎT (A+B)=С, где  , i=1,2,...,n, j=1,2,...,n.
, i=1,2,...,n, j=1,2,...,n.
Например,  .
.
Определение. Произведением квадратной матрицы А на число к, будем называть квадратную матрицу к×А, каждый элемент которой равен к×аij, где аij– элемент i-ой строки и j-го столбца матрицы А.
Например, 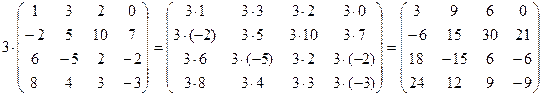 .
.
Определение. Разностью матриц В и А называется матрица Х=В-А, такая что А+Х=В.
Например, 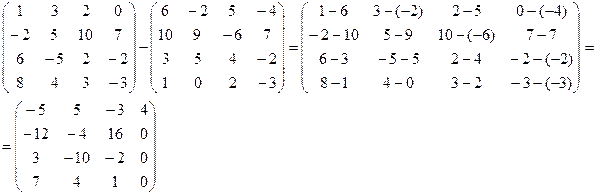 .
.
Определение. Матрица (-А)=-1×А называется противоположной матрице А.
Например, матрица 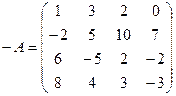 является противоположной матрице
является противоположной матрице  .
.
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А+В=В+А (коммутативность сложения матриц).
2. А+(В+С)=(А+В)+С (ассоциативность сложения матриц).
3. А+О=А
4. А+(-А)=О
5. 1×А=А
6. к×(А+В)=к×А+к×В (дистрибутивность сложения матриц относительно умножения матрицы на число)
7. (к+t)×A=к×А+t×A
8. к×(t×A)=(к×t)×A
Определение. Под произведением квадратных матриц А и В будем понимать матрицу С, у которой элемент, стоящий на пересечении i строки и j столбца, получен как сумма произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
"A,BÎT (A´B)=С, где 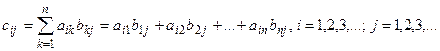
Например, найдем произведение квадратных матриц третьего порядка: 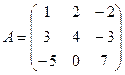 ;
; 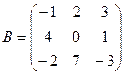 . Пусть A´B=С. Найдем по определению каждый элемент матрицы с:
. Пусть A´B=С. Найдем по определению каждый элемент матрицы с:
с11=а11×b11+a12×b21+a13×b31=1×(-1)+2×4+(-2) ×(-2)=11;
с12=а11×b12+a12×b22+a13×b32=1×2+2×0+(-2) ×7=-12;
с13=а11×b13+a12×b23+a13×b33=1×3+2×1+(-2) ×(-3)=11;
с21=а21×b11+a22×b21+a23×b31=3×(-1)+4×4+(-3) ×(-2)=19;
с22=а21×b12+a22×b22+a23×b32=3×2+4×0+(-3) ×7=-15;
с23=а21×b13+a22×b23+a23×b33=3×3+4×1+(-3_×(-3)=22;
с31=а31×b11+a32×b21+a33×b31=-5×(-1)+0×4+7×(-2)=-9;
с32=а31×b12+a32×b22+a33×b32=-5×2+0×0+7×7=4;
с33=а31×b13+a32×b23+a33×b33=-5×3+0×1+7×(-3)=-36;
Таким образом, матрица 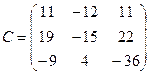 .
.
Определение. Если A´B=В´А, то матрицы А и В называются перестановочными или коммутирующими.
Не всякие две матрицы являются перестановочными. Единичная матрица перестановочна с любой матрицей.
Умножение матриц обладает следующими свойствами.
1. A´(B´С)=(A´B)´С
2. (А+В)´С=А´С+В´С
3. С´(А+В)= С´А+С´В
4. к×(A´B)= (к×A)´B
Определение. Пусть А – квадратная матрица, n³0 некоторое целое число. Аn – n-ая степень матрицы А, причем 1) А0=Е; 2) А1=А; 3) Аn = А´А´…´А (n раз) при n³2.
Например, 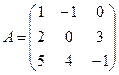 ;
; 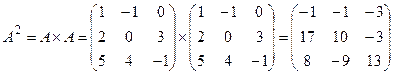
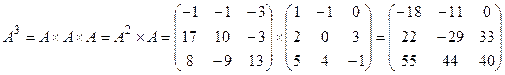 и так далее.
и так далее.
Операция сложения на множестве прямоугольных матриц определяется аналогично операции сложения квадратных матриц, с тем условием, что число строк первой матрицы равно числу строк второй, число столбцов первой матрицы равно числу столбцов второй.
Операция умножения прямоугольных матриц определяется аналогично операции умножения квадратных матриц при том условии, что число столбцов первой матрицы должно быть равно числу строк второй матрицы. (То есть умножать можно прямоугольную матрицу А размера m´n на прямоугольную матрицу В размера n´t. При этом матрица А´В будет иметь размер m´t.)
Пример выполнения заданий практической части
Пример 1. Даны матрицы 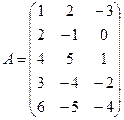 ;
; 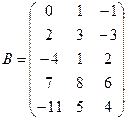 ;
; 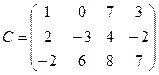 . Найти сумму А+В и произведение А´С.
. Найти сумму А+В и произведение А´С.
Решение.
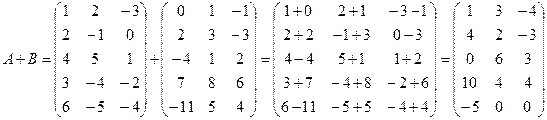 .
.
Пусть А´С=D. Тогда
d11=1×1+2×2+(-3) ×(-2)=11
d12=1×0+2×(-3)+(-3) ×6=-24
d13=1×7+2×4+(-3) ×8=-9
d14=1×3+2×(-2)+(-3) ×7=-22
d21=2×1+(-1) ×2+0×(-2)=0
d22=2×0+(-1) ×(-3)+0×6=3
d23=2×7+(-1) ×4+0×8=10
d24=2×3+(-1) ×(-2)+0×7=8
d31=4×1+5×2+1×(-2)=12
d32=4×0+5×(-3)+1×6=-9
d33=4×7+5×4+1×8=56
d34=4×3+5×(-2)+1×7=9
d41=3×1+(-4) ×2+(-2) ×(-2)=-1
d42=3×0+(-4) ×(-3)+(-2) ×6=0
d43=3×7+(-4) ×4+(-2) ×8=-11
d44=3×3+(-4) ×(-2)+(-2) ×7=3
d51=6×1+(-5) ×2+(-4) ×(-2)=4
d52=6×0+(-5) ×(-3)+(-4) ×6=-9
d53=6×7+(-5) ×4+(-4) ×8=-10
d54=6×3+(-5) ×(-2)+(-4) ×7=0.
Таким образом, 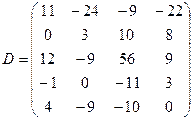 .
.
Пример 2. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если 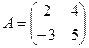 ,
, 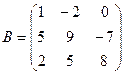 ,
, 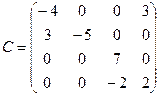 .
.
Решение.
- Найдем значение многочлена от матрицы А.
1) 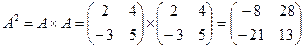 ;
;
2)  ;
;
3) 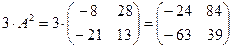 ;
;
4) 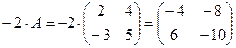 ;
;
5) 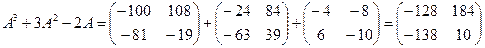 .
.
2. Найдем значение многочлена от матрицы В.
1) 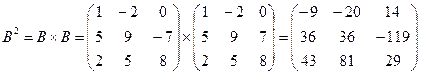 ;
;
2)  ;
;
3) 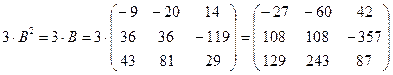 ;
;
4)  ;
;
5) 
3. Найдем значение многочлена от матрицы С.
1) 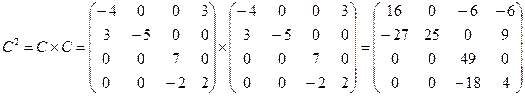 ;
;
2) 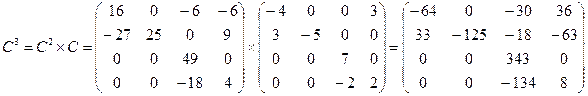 ;
;
3) 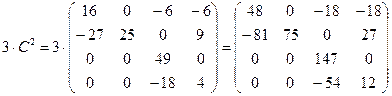 ;
;
4) 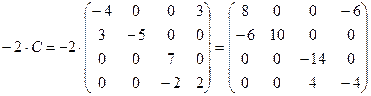
5) 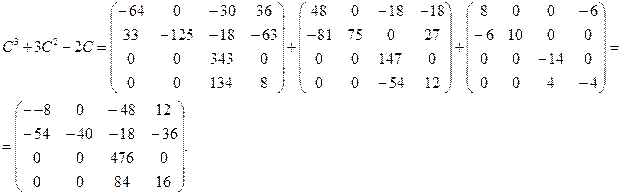
Ответ: 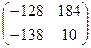 ;
; 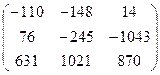 ;
; 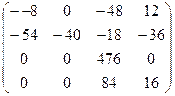 .
.
Пример 3. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70 ден. ед., а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
| 1 | 20 | 35 | 10 |
| 2 | 15 | 27 | 8 |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
 ,
, 
Тогда матрица затрат на перевозки будет иметь вид 
 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Задания для аудиторного занятия
1. Найти матрицу 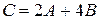 , если
, если 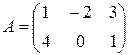 ,
, 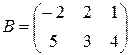 .
.
2.Заданы матрицы А, В, С. Найти произведения А´В, В´С, А´С, А´В´С.
2.1 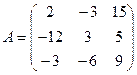 ,
, 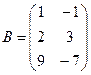 ,
, 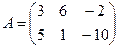 ;
;
2.2. 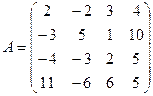 ,
, 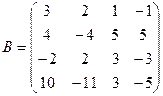 ,
, 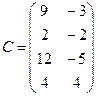 .
.
3. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если  ,
, 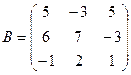 ,
, 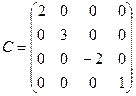 .
.
4. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей-строкой X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица-строка С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица-строка P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
Сколько метров ткани каждого типа потребуется для выполнения плана?
1.4. Домашнее задание
1. Найти матрицу Х если:
1.1. 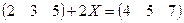 ;
;
1.2. 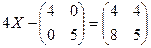 .
. 
2. Найти произведения матриц:
2.1. 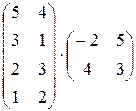 ; 2.2.
; 2.2. 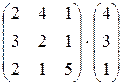 ;
;
2.3. 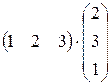 .
.
3. Вычислить 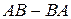 , если
, если 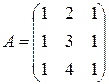 ,
, 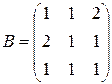 .
.
4. Найти значение многочлена f(x)=ху2+3х2 у-2ух от матриц Х, У, если
4.1. 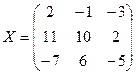 ,
, 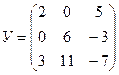 ;
;
4.2. 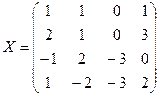 ,
, 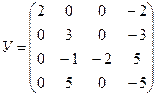 .
.
5. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей (вектором) X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица (вектор) С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица (вектор) P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
5.1. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
5.2. Определить стоимость всей ткани, необходимой для выполнения плана.
5.3. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Дата: 2019-02-02, просмотров: 339.