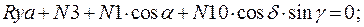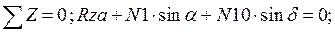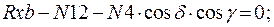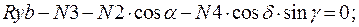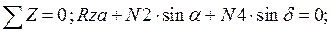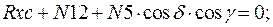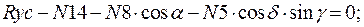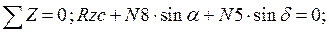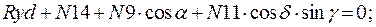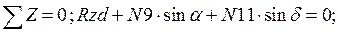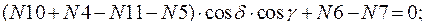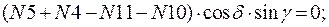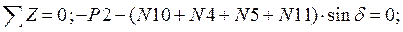Цель работы: изучить применение метода конечных разностей для расчета балочных систем.
Порядок выполнения работы:
1) разбить пролет балки на заданное число частей, приняв граничные точки участков в качестве расчетных точек метода конечных разностей;
2) используя дифференциальные уравнения равновесия изгибаемых стержневых систем и метод конечных разностей, определить прогибы расчетных точек и изгибающие моменты в соответствующих (этим точкам) сечениях балки;
3) построить эпюру изгибающих моментов и график прогибов балки.
Примечание: все необходимые расчеты выполнить в системе компьютерной алгебры MathCAD.
Методика расчета.
Для расчета стержневых изгибаемых систем могут использоваться три
варианта дифференциальных уравнений равновесия:
1) 
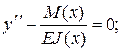(10.1)
2) 
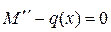, (10.2)
3) 
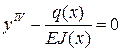, (10.3)
которые в конечных разностях для i-ой точки (рис. 10.1) имеют вид [2]:
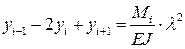; (10.4)
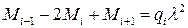; (10.5)
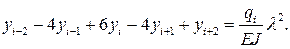(10.6)
Переходя от дифференцирования к конечным разностям мы должны
разбить систему (балку) на заданное число конечных участков, граничные
точки между которыми принимаются за расчетные точки (сечения). Для расчетных точек, в которых определяемые величины (перемещения, усилия) неизвестны, и необходимо записывать уравнения (10.4)– (10.6). При этом, как несложно увидеть, в уравнениях будут появляться перемещения (усилия) в так называемых законтурных точках (например, в точках -1 и 7 на рис. 10.1). Для определения этих величин могут использоваться граничные условия сооружений, то есть известные значения перемещений и усилий на границах сооружения, связанные с условиями закрепления крайних точек системы:
1) шарнирное опирание (рисунок 10.2):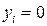 
и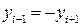 
;
2) защемление (рисунок 10.3):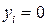 
и 
.
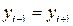Рисунок 10.2 Рисунок 10.3
Пример расчета. Рассмотрим применение метода конечных разностей
к решению задачи изгиба двухопорной балки, нагруженной распределенной (по треугольному закону) нагрузкой (рисунок 10.4).
Определим вначале изгибающие моменты в системе, для чего воспользуемся вначале уравнением (10.2) –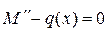 
, которое в конечных разностях представлено в (10.5).
Разобьем балку на четыре части (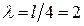 
м) и составим уравнения (9.5) для точек 1, 2 и 3 (последовательно принимая i равным номерам
Рисунок 10.4 этих точек):
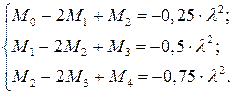(10.7)
Согласно граничным условиям при этом будем иметь: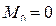 
и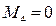 
.
Учитываем граничные условия и решаем систему уравнений (10.7). Находим:
; 
; 
.
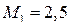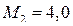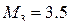Для определения прогибов системы воспользуемся теперь уравнением (10.1), которое в конечных разностях для произвольного i-го узла имеет вид (10.4).
Записав уравнение (10.4) для точек 1, 2 и 3, получим систему уравнений:
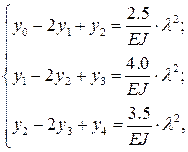
решая которую, с учетом граничных услови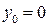й ( 
и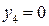 
), найдем:
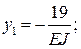
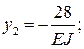
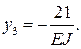
Процедура расчета рассматриваемой задачи в системе компьютерной алгебры MathCAD (см. с. 47).
По полученным результатам строим эпюру изгибающих моментов и график прогибов балки (см. рис. 10.5).
Выполнив анализ результатов расчета, можно сделать следующие выводы:
– в методе конечных разностей густота разбивки системы определяет точность решения;
– наибольший изгибающий момент в рассматриваемой балке возникает между сечениями 2 и 3;
– наибольший прогиб при рассматриваемом нагружении балки возникает между точками 2 и 3.
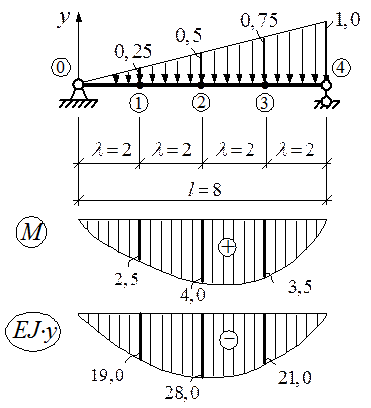
Рисунок 10.5
Лабораторная работа № 11
Применение общей системы равновесия строительной механики
к расчету пространственной ферменной структуры
Цель работы: изучить применение общей системы равновесия строительной механики к расчету пространственной ферменной структуры.
Порядок выполнения работы:
1) обозначить приложенную к ферменной структуре нагрузку и реакции в опорах;
2) пронумеровать стержни ферменной структуры;
3) вырезая каждый узел ферменной структуры, составить общую систему равновесия;
4) решить систему уравнений в системе компьютерной алгебры MathCAD;
5) сделать проверку, используя три уравнения равновесия ферменной структуры в целом.
Пример расчета. Рассмотрим расчет ферменной структуры, представленной на рис. 11.1.
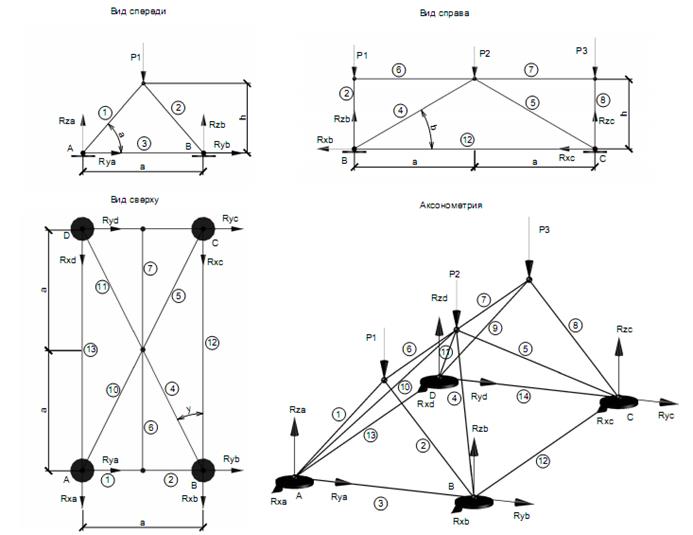
Рисунок 11.1
Будем считать, что нагрузка может быть приложена только в узлы верхних элементов ферменной структуры, поэтому обозначим внешнюю нагрузку в виде сосредоточенных сил (P1, P2, P3). Для удобства пронумеруем стержни фермы (1–14). Обозначим реакции в опорах (RXA, RYA, RZA, RXB, RYB, RZB, RXC, RYC, RZC, RXD, RYD, RZD,).
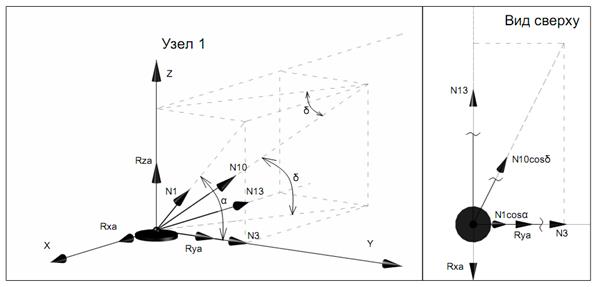
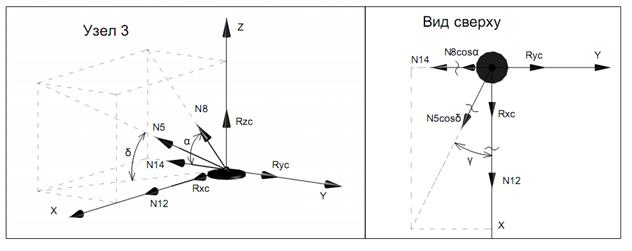
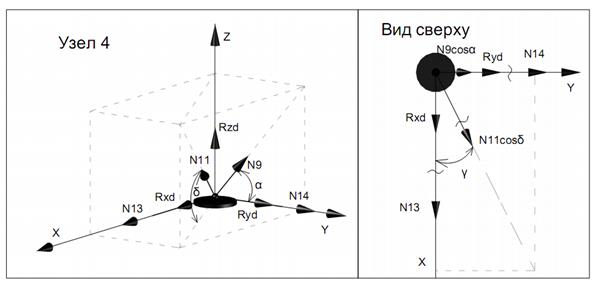
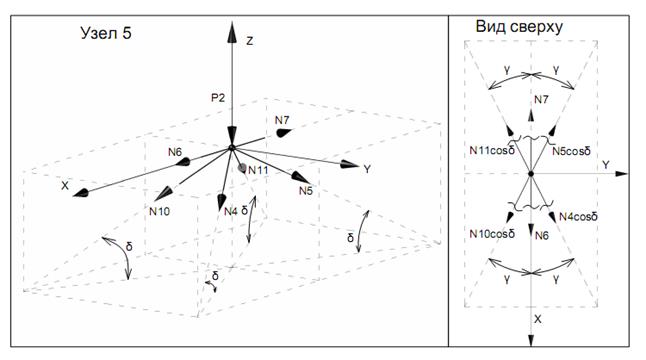
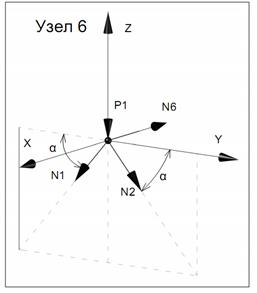
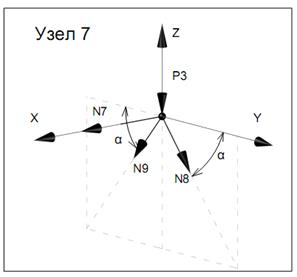
Вырезая каждый узел фермы, обозначим неизвестные продольные усилия стержней фермы (N1, N2, N3, … и т.д., рис. 11.2).
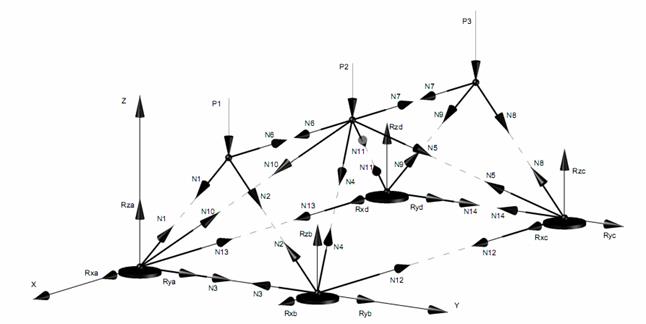
Рисунок 11.2
Составим уравнение равновесия для каждого узла ферменной структуры проецируя усилия и нагрузки на соответствующие оси.( 
)
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| 
|
 
 
| 
|
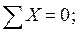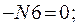
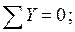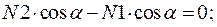
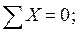
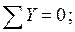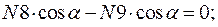
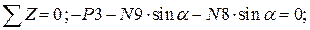
Для определения неизвестных усилий и реакций, решим систему уравнений, составленную из полученных ранее уравнений равновесия узлов фермы.
Проверка: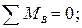 
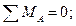
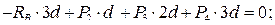
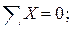
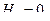
Расчеты произведем в системе компьютерной алгебры MathCAD.
ЛИТЕРАТУРА,
рекомендуемая для расширенного изучения материала
1. Ильин, В.П. Численные методы решения задач строительной механики / В.П. Ильин, В.В. Карпов, А.М. Масленников. – Мн. : Выш. школа, 1990.– 349 с.
2. Масленников, А.М. Расчет строительных конструкций численными методами: учебное пособие. – Л. : Изд-во Ленингр. ун-та, 1987. - 224 с.
3. Турчак, Л.И. Основы численных методов : учебное пособие. – М. : Наука, 1987. - 320 с.
4. Борисевич, А.А. Строительная механика : учебное пособие / А.А. Борисевич, Е.М. Сидорович, В.И. Игнатюк. – Минск: БНТУ, 2007. – 821 с.
5. Зенкевич, О. Метод конечных элементов в технике. - М.: Мир, 1975.-554с.
6. Игнатюк, В.И., Бочарова, Н.В. Численные методы решения задач строительной механики : учебное пособие. – Брест: БрГТУ, 2015. – 100 с.
7. Караманский, Т.Д. Численные методы строительной механики / Пер с болг. ; под ред. Г.К. Клейна. – М. : Стройиздат, 1981. - 436 с.
8. Матричные алгоритмы в строительной механике стержневых систем : учебное пособие / Д.К. Бендюг и др. – М. : Высшая школа, 1980. – 124 c.
9. Самарский, А.А. Введение в численные методы : учебное пособие. –
М. : Наука, 1987. - 288 с.
Содержание
| Введение…………………………………………………………………………. | 3 |
| Лабораторная работа № 1. Применение общей системы равновесия строительной механики к расчету статически определимых ферм…………... | 4 |
| Лабораторная работа № 2. Использование матриц влияния в расчетах ферм | 7 |
| Лабораторная работа № 3. Применение общей системы равновесия строительной механики к расчету статически определимых многопролетных балок………………………………………………………………………. | 12 |
| Лабораторная работа № 4. Применение общей системы равновесия строительной механики к расчету статически определимых рам…………….. | 17 |
| Лабораторная работа № 5. Расчет усилий в трехшарнирных арках…………. | 21 |
| Лабораторная работа № 6. Определение перемещений в трехшарнирных арках………………………………………………………………………… | 26 |
| Лабораторная работа № 7. Деформированный вид арки……………………... | 31 |
| Лабораторная работа № 8. Расчет двухшарнирной арки с использование численного интегрирования………………………………………………. | 34 |
| Лабораторная работа № 9. Матричная форма определения перемещений в рамах………………………………………………………………………... | 39 |
| Лабораторная работа № 10. Расчет балок методом конечных разностей….. | 43 |
| Литература, рекомендуемая для расширенного изучения материала……….. | 47 |
Учебное издание
Игнатюк Валерий Иванович
Бочарова Наталья Владимировна
Лабораторные работы
по дисциплине «Численные методы решения задач»
Методические указания для студентов специальности
1-70 02 01 «Промышленное и гражданское строительство»
1-74 04 01 «Сельское строительство и обустройство территорий»
дневной и заочной форм обучения
Ответственный за выпуск Игнатюк В.И.
Редактор Боровикова Е.А.
Компьютерный набор и верстка Игнатюк В.И.
Корректор Никитчик Е.В.
Издательство БрГТУ. Лицензия № от 18.03.2016. Подписано к печати 25.03.2016. Формат 60 
84/16. Бумага Снегурочка. Гарнитура Times New Roman. Усл. печ. л. 8,8. Уч.-изд. л. 9,5. Тираж 200 зкз. Заказ № . Отпечатано на ризографе Учреждения образования «Брестский государственный технический университет». 224017, Брест, ул. Московская, 267.
Игнатюк В. И., Бочарова Н. В.
Лабораторные работы
по дисциплине
«Численные методы
решения задач»
Б р е с т 2 0 1 7
Дата: 2019-02-02, просмотров: 691.
