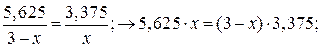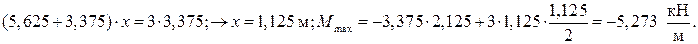Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Цель работы: изучить использование матриц влияния на примере расчета статически определимых ферм.

Порядок выполнения работы:

1) составить матрицу влияния для заданной фермы;

2) рассчитать усилия фермы с единичной нагрузкой во всех узлах фермы, а также рассчитать 2–4 примера с различной заданной нагрузкой (симметричной и несимметричной);

3) для всех примеров сделать рисунки с изображением полученных внутренних усилий в ферме;

4) сравнить полученные результаты расчета с результатами, полученными с помощью методики расчета фермы лабораторной работы № 1;

5) сделать выводы (проанализировать в каких стержнях возникает наибольшее усилие).

Методика расчета. При проведении расчетов, ориентированных на компьютерные технологии, в строительной механике применяют дискретные расчетные схемы и методы матричного исчисления. Для примера такого подхода рассмотрим расчет фермы с помощью матрицы влияния продольных усилий.

Действующие на ферму нагрузки представим в виде вектора нагрузок (2.1), компонентами которого являются значения заданных нагрузок (P ₁ .. P_t), пронумерованных в определенном порядке. Результатом расчета будет служить вектор усилий, в котором в заданном порядке будут перечислены значения продольных усилий в конкретных стержнях фермы (N₁.. N_s).

     

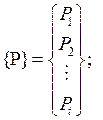
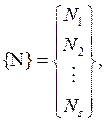
где t – количество действующих нагрузок; s – количество стержней фермы.

Матрица влияния продольных усилий фермы записывается в виде:

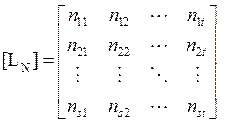
Каждый элемент n_ik  матрицы влияния представляет собой величину продольного усилия в i-ом стержне фермы при действии на ферму только одной единичной нагрузки P_k = 1.

Вектор продольных усилий в стержнях фермы {N} будет определяться произведением матрицы влияния фермы [L_N] на вектор нагрузок {P}.

{N} = [L_N] ∙ {P}.                                                (2.1)

Пример расчета. Для примера рассмотрим расчет фермы, рассмотренной ранее в лабораторной работе № 1 (рис. 2.1).

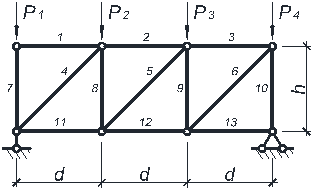
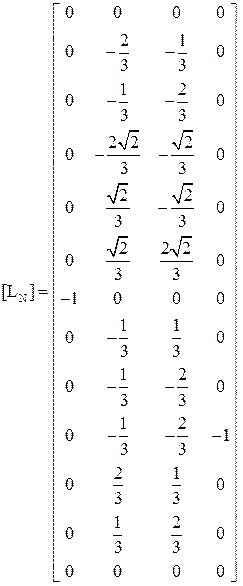Рисунок 2.1

Составим матрицу влияния фермы. Так как в данной ферме 13 стержней и к ней приложено 4 внешних силы, то матрица влияния будет иметь размеры 4 x 13.

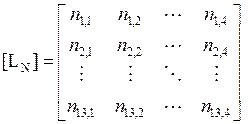
Для определения элементов n_{i , k} матрицы влияния данной фермы необходимо поочередно просчитать значения внутренних усилий в каждом i-ом стержне фермы при поочередном действии на ферму единичных нагрузок P_k=1, параллельно заполняя соответствующие столбцы матрицы влияния:

при P₁=1; P₂=0; P₃=0; P₄=0 (1 столбец);

при P₁=0; P₂=1; P₃=0; P₄=0 (2 столбец);

при P₁=0; P₂=0; P₃=1; P₄=0 (3 столбец);

при P₁=0; P₂=0; P₃=0; P₄=1 (4 столбец).

Матрица влияния принимает вид:

 

 

Используя полученную матрицу влияния, выполним примеры расчета фермы на различную нагрузку в системе компьютерной алгебры MathCAD:

а) при P₁=1; P₂=1; P₃=1; P₄=1;

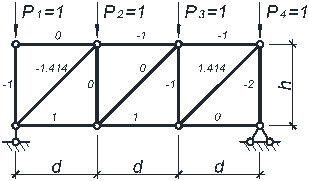
б) при P₁=10; P₂=20; P₃=30; P₄=40 (несимметричное нагружение);

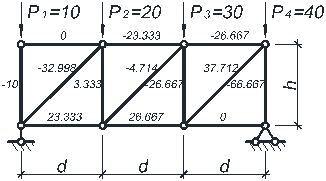
в) при P₁=30; P₂=20; P₃=20; P₄=30 (симметричное нагружение);

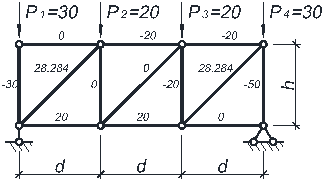
Проанализировав результаты расчетов, можно сделать следующие выводы:

- наиболее растянутые стержни: № 6 (N₆ = 37.712) – при несимметричном нагружении, № 6 (N₆ = 28.284) – при симметричном нагружении;

- наиболее сжатые стержни – № 10 (N₁₀ = -66.667) – при несимметричном нагружении, № 10 (N₁₀ = -50) – при симметричном нагружении;

- сравнивая полученные результаты расчета с результатами, полученными с помощью методики расчета фермы лабораторной работы № 1, видим, что они совпадают.

Расчеты произведем в системе компьютерной алгебры MathCAD .

 

 

 

Лабораторная работа № 3

Применение общей системы равновесия строительной механики
к расчету статически определимых многопролетных балок

Цель работы: изучить применение общей системы равновесия строительной механики к расчету статически определимых многопролетных балок и решение систем линейных алгебраических уравнений.

Порядок выполнения работы:

1) разделить балку по шарнирам на простые балки (получим в качестве неизвестных в шарнирах внутренние силы и опорные реакции), показав усилия взаимодействия между ними;

2) получить общую систему уравнений равновесия рамы, составив уравнения равновесия для каждой простой балки;

3) определить усилия в простых балках и опорные реакции, решив полученную систему линейных алгебраических уравнений в системе компьютерной алгебры MathCAD;

4) построить эпюры усилий M, Q, N  для каждой балки в отдельности и для всей многопролетной балки;

5) выполнить проверку выполнения общих закономерностей изменения эпюр усилий и статическую проверку.

Пример расчета.

Рассмотрим расчет многопролетной балки, показанной на рисунке 3.1

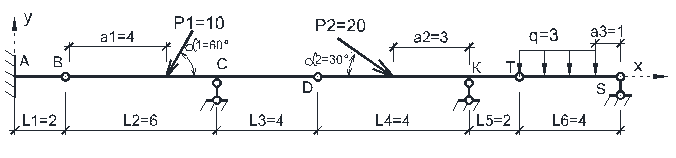Рисунок 3.1

Каждая из простых балок – это диск, который имеет три степени свободы, равновесие которого описывается тремя уравнениями равновесия. Каждый шарнир, соединяющий балки, имеет две связи и при его разрезании в нем возникает соответственно две внутренние реактивные силы. Рассматриваемая многопролетная балка состоит из четырех простых балок, и для них соответственно можно составить двенадцать уравнений равновесия. Разделив многопролетную балку по трем шарнирам B, D, T на простые балки, получим в качестве неизвестных шесть внутренних реактивных сил и шесть опорных реакций в опорах.

Разобьём балку на простые балки. Обозначим реакции опор R _А, H_A, M_RA, R_С, R_К ,R_S и неизвестные в шарнирах  X_B, Y_B , X_D, Y_D , X_T, Y_T . (рис. 3.2).

Используя общий подход, следует составить уравнения равновесия для каждой из простых балок:

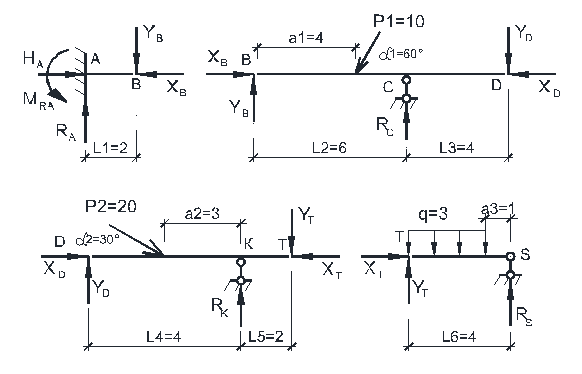
Рисунок 3.2

Для определения неизвестных усилий и реакций, решим систему уравнений, составленную уравнений равновесия для простых балок:

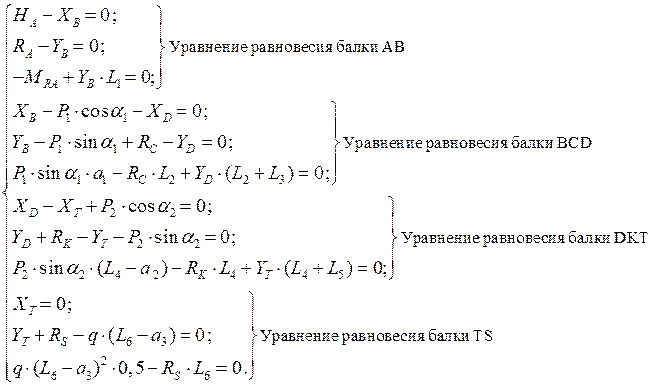
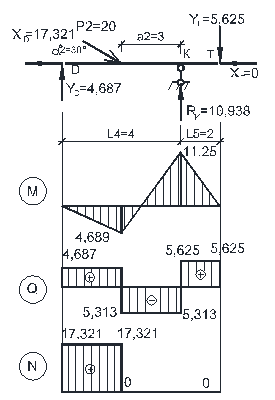
После определения значений усилий, строим эпюры M, Q, N (рис. 3.4). При этом необходимо выполнить проверку выполнения общих закономерностей изменения эпюр.

Для статической проверки составим три уравнения равновесия балки в целом, подставив полученные значения опорных реакций:

      

      

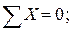
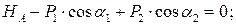
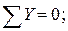
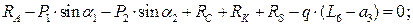
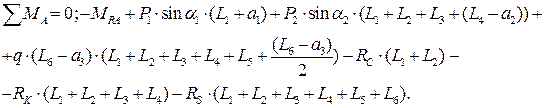
Расчеты произведем в системе компьютерной алгебры MathCAD.

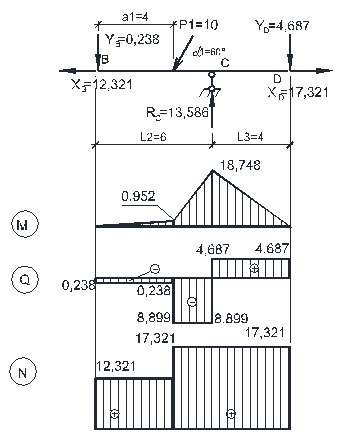
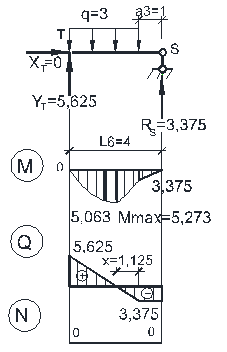
Теперь можно рассмотреть каждую балку отдельно с приложенными внешними нагрузками, опорными реакциями и усилиями между соседними балками (в шарнирах) и построить для каждой из них эпюры внутренних сил М, Q, N. Совместив эпюры усилий во всех простых балках на одной схеме, получим эпюры внутренних сил М, Q, N для многопролетной балки (рис.3.3).

Определим экстремум в балке TS:

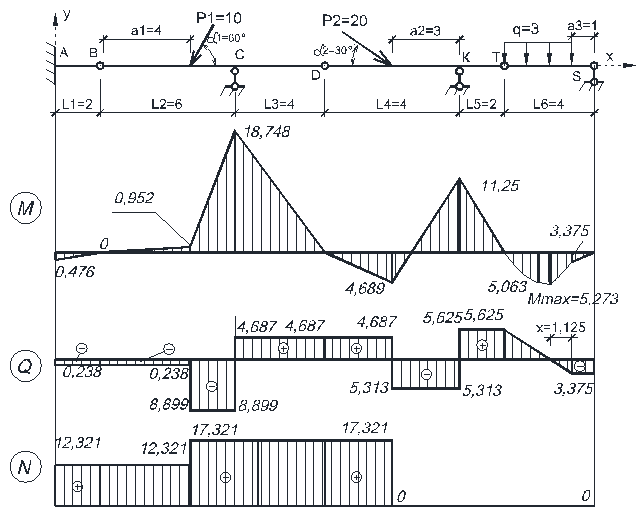
Рисунок 3.3

 

Лабораторная работа № 4

Применение общей системы равновесия строительной механики
к расчету статически определимых рам

Цель работы: изучить применение общей системы равновесия строительной механики к расчету статически определимых рам и решение систем линейных алгебраических уравнений.

Порядок выполнения работы:

1) разбить раму на простые стержни (прямолинейные элементы, в пределах которых нет изменения нагрузок), показав усилия взаимодействия между ними;

2) получить общую систему уравнений равновесия рамы, составив уравнения равновесия для каждого из стержней;

3) определить усилия в стержнях рамы, решив полученную систему линейных алгебраических уравнений в системе компьютерной алгебры MathCAD;

4) построить эпюры усилий M, Q, N рамы;

5) выполнить проверку выполнения общих закономерностей изменения эпюр усилий и статическую проверку.

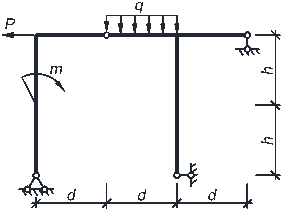
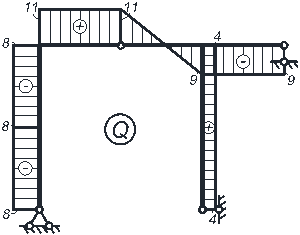
Пример расчета. Рассмотрим расчет рамы, представленной на рис. 4.1
(при d = 2м; h = 2м; P = 4кН;
m = 10кНм; q = 10кН/м).

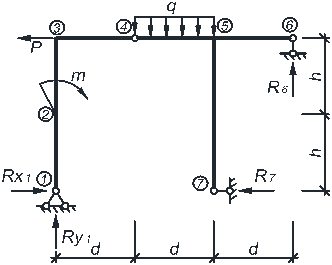Разобьём раму на простые стержни, нумеруя узлы их соединения (1–7). Обозначим реакции опор Rx₁, Ry₁, R₆, R₇ (рис. 4.2).

Рисунок 4.1

Рисунок 4.2

Вырезая каждый стержень, обозначим неизвестные внутренние усилия стержней рамы в характерных сечениях через x_i, y_i (продольные и
поперечные усилия) и z_i (моменты),
где i – номер характерного сечения.
(рис. 3.3). В случае соединения трех стержней в одном узле, вторую пару внутренних усилий будем обозначать через 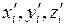(см. узел 5).

В шарнирных соединениях отсутствуют моменты, поэтому там обозначаем только продольные и поперечные усилия (в узле 4 – x₄, y₄).

 

При наличии сосредоточенной нагрузки или момента в узле, относим их к тому стержню, конечная точка которого примыкает к данному сечению (в нашем примере: внешний момент m относим к стержню 1-2; сосредоточенную нагрузку P – к стержню 2-3).

Рисунок 4.3

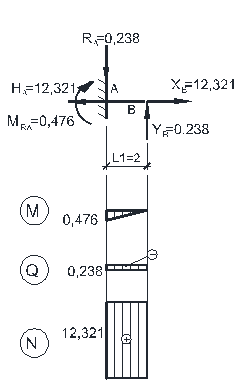
Составим уравнения равновесия для каждого стержня рамы, проецируя усилия и нагрузки на соответствующие оси. Суммы моментов берем относительно начальных сечений стержней.

Стержень 1-2: 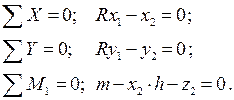Стержень 2-3: 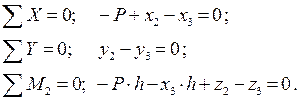Стержень 3-4:

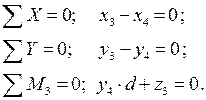
Стержень 4-5: 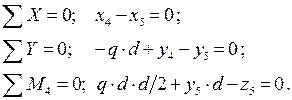Стержень 5-6: 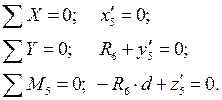Стержень 5-7:

 

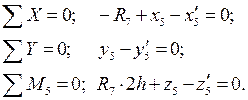
Для определения неизвестных усилий и реакций, решим систему уравнений, составленную из полученных ранее уравнений равновесия стержней рамы:

Рисунок 4.4

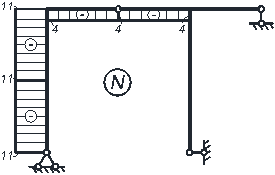
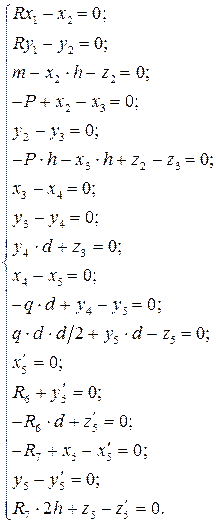
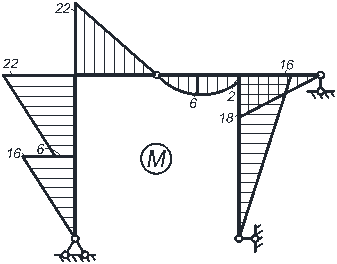
После определения значений усилий, строим эпюры M, Q, N (рис. 4.4). При этом необходимо выполнить проверку выполнения общих закономерностей изменения эпюр.

Для статической проверки составим три уравнения равновесия рамы, подставив полученные значения опорных реакций:

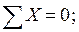
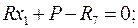
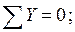
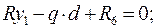
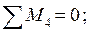
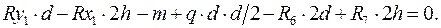
Расчеты произведем в системе компьютерной алгебры MathCAD.

 

 

Лабораторная работа № 5