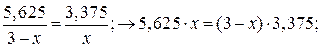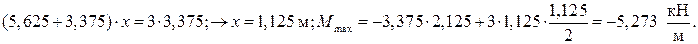Лабораторная работа № 3
Применение общей системы равновесия строительной механики
к расчету статически определимых многопролетных балок
Цель работы: изучить применение общей системы равновесия строительной механики к расчету статически определимых многопролетных балок и решение систем линейных алгебраических уравнений.
Порядок выполнения работы:
1) разделить балку по шарнирам на простые балки (получим в качестве неизвестных в шарнирах внутренние силы и опорные реакции), показав усилия взаимодействия между ними;
2) получить общую систему уравнений равновесия рамы, составив уравнения равновесия для каждой простой балки;
3) определить усилия в простых балках и опорные реакции, решив полученную систему линейных алгебраических уравнений в системе компьютерной алгебры MathCAD;
4) построить эпюры усилий M, Q, N для каждой балки в отдельности и для всей многопролетной балки;
5) выполнить проверку выполнения общих закономерностей изменения эпюр усилий и статическую проверку.
Пример расчета.
Рассмотрим расчет многопролетной балки, показанной на рисунке 3.1
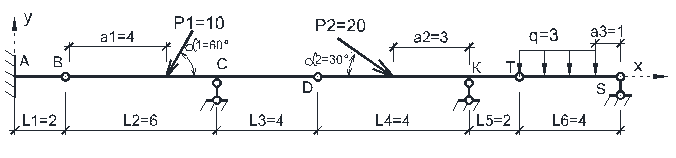 Рисунок 3.1
Рисунок 3.1
Каждая из простых балок – это диск, который имеет три степени свободы, равновесие которого описывается тремя уравнениями равновесия. Каждый шарнир, соединяющий балки, имеет две связи и при его разрезании в нем возникает соответственно две внутренние реактивные силы. Рассматриваемая многопролетная балка состоит из четырех простых балок, и для них соответственно можно составить двенадцать уравнений равновесия. Разделив многопролетную балку по трем шарнирам B, D, T на простые балки, получим в качестве неизвестных шесть внутренних реактивных сил и шесть опорных реакций в опорах.
Разобьём балку на простые балки. Обозначим реакции опор R А, HA, MRA, RС, RК ,RS и неизвестные в шарнирах XB, YB , XD, YD , XT, YT . (рис. 3.2).
Используя общий подход, следует составить уравнения равновесия для каждой из простых балок:
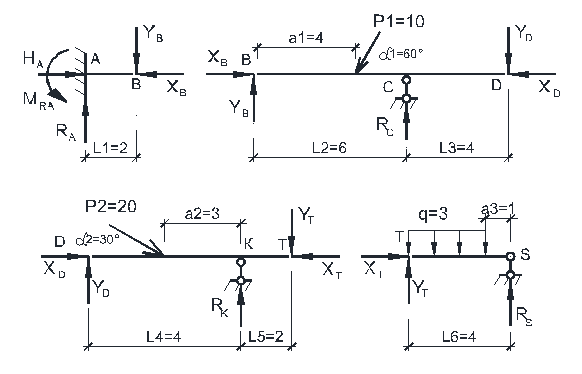
Рисунок 3.2
Для определения неизвестных усилий и реакций, решим систему уравнений, составленную уравнений равновесия для простых балок:
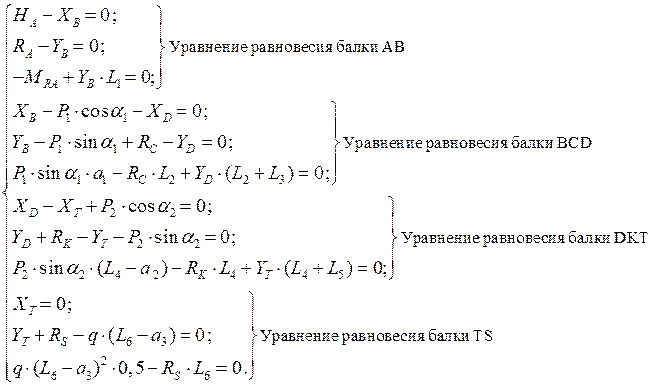
После определения значений усилий, строим эпюры M, Q, N (рис. 3.4). При этом необходимо выполнить проверку выполнения общих закономерностей изменения эпюр.
Для статической проверки составим три уравнения равновесия балки в целом, подставив полученные значения опорных реакций:
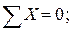
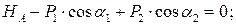
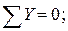
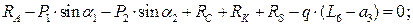

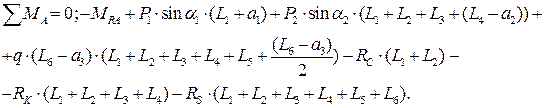
Расчеты произведем в системе компьютерной алгебры MathCAD.
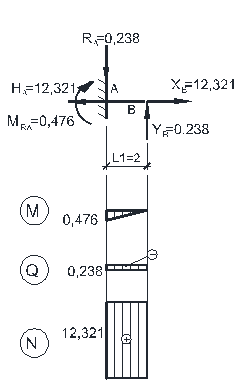
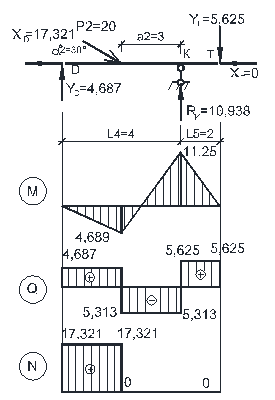
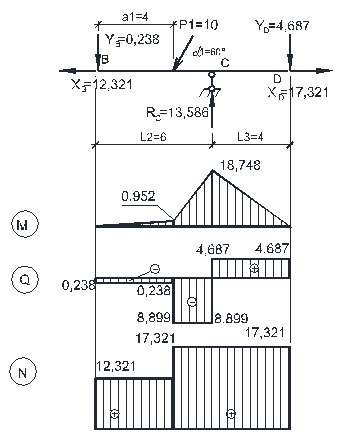
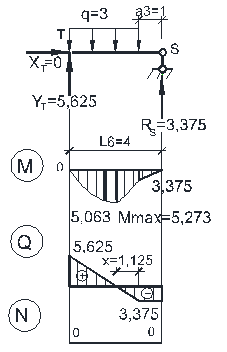
Теперь можно рассмотреть каждую балку отдельно с приложенными внешними нагрузками, опорными реакциями и усилиями между соседними балками (в шарнирах) и построить для каждой из них эпюры внутренних сил М, Q, N. Совместив эпюры усилий во всех простых балках на одной схеме, получим эпюры внутренних сил М, Q, N для многопролетной балки (рис.3.3).
| Определим экстремум в балке TS:
| |
|
| 
|
| |
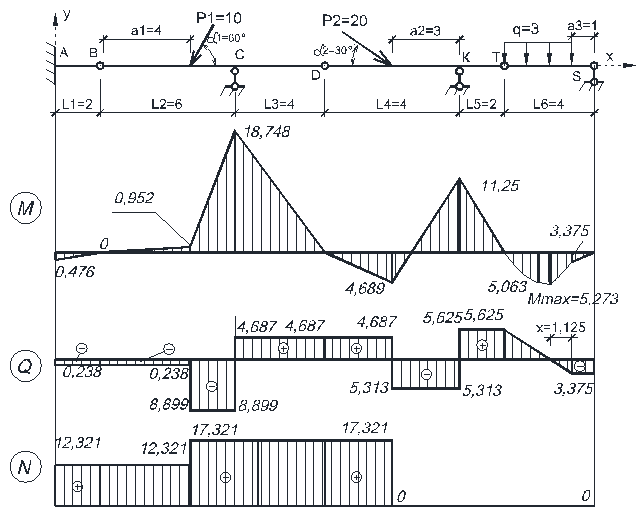
Рисунок 3.3
Лабораторная работа № 4
Применение общей системы равновесия строительной механики
к расчету статически определимых рам
Цель работы: изучить применение общей системы равновесия строительной механики к расчету статически определимых рам и решение систем линейных алгебраических уравнений.
Порядок выполнения работы:
1) разбить раму на простые стержни (прямолинейные элементы, в пределах которых нет изменения нагрузок), показав усилия взаимодействия между ними;
2) получить общую систему уравнений равновесия рамы, составив уравнения равновесия для каждого из стержней;
3) определить усилия в стержнях рамы, решив полученную систему линейных алгебраических уравнений в системе компьютерной алгебры MathCAD;
4) построить эпюры усилий M, Q, N рамы;
 5) выполнить проверку выполнения общих закономерностей изменения эпюр усилий и статическую проверку.
5) выполнить проверку выполнения общих закономерностей изменения эпюр усилий и статическую проверку.
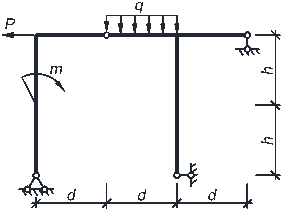
Пример расчета. Рассмотрим расчет рамы, представленной на рис. 4.1
(при d = 2м; h = 2м; P = 4кН;
m = 10кНм; q = 10кН/м).
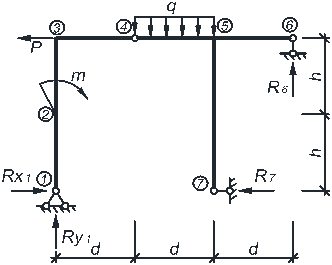 Разобьём раму на простые стержни, нумеруя узлы их соединения (1–7). Обозначим реакции опор Rx1, Ry1, R6, R7 (рис. 4.2).
Разобьём раму на простые стержни, нумеруя узлы их соединения (1–7). Обозначим реакции опор Rx1, Ry1, R6, R7 (рис. 4.2).
|
|
поперечные усилия) и zi (моменты),
где i – номер характерного сечения.
(рис. 3.3). В случае соединения трех стержней в одном узле, вторую пару внутренних усилий будем обозначать через
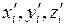 (см. узел 5).
(см. узел 5).
В шарнирных соединениях отсутствуют моменты, поэтому там обозначаем только продольные и поперечные усилия (в узле 4 – x4, y4).
При наличии сосредоточенной нагрузки или момента в узле, относим их к тому стержню, конечная точка которого примыкает к данному сечению (в нашем примере: внешний момент m относим к стержню 1-2; сосредоточенную нагрузку P – к стержню 2-3).
|
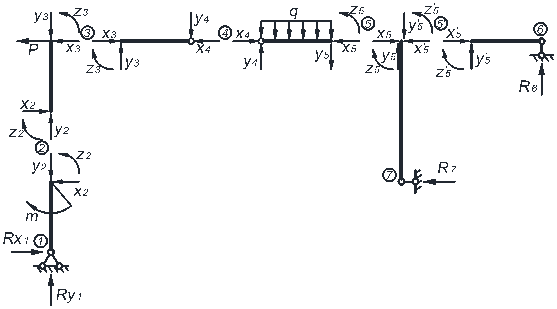
Составим уравнения равновесия для каждого стержня рамы, проецируя усилия и нагрузки на соответствующие оси. Суммы моментов берем относительно начальных сечений стержней.
Стержень 1-2:
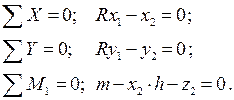 Стержень 2-3:
Стержень 2-3:
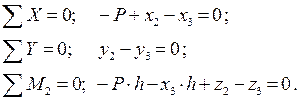 Стержень 3-4:
Стержень 3-4:
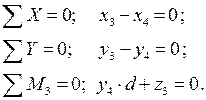
| Стержень 4-5:
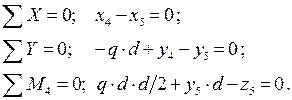 Стержень 5-6:
Стержень 5-6:
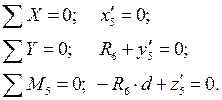 Стержень 5-7:
Стержень 5-7:
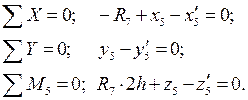
|
Для определения неизвестных усилий и реакций, решим систему уравнений, составленную из полученных ранее уравнений равновесия стержней рамы:
|
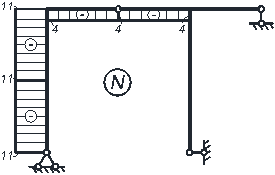
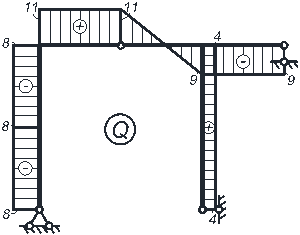
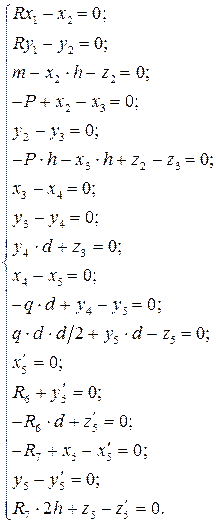
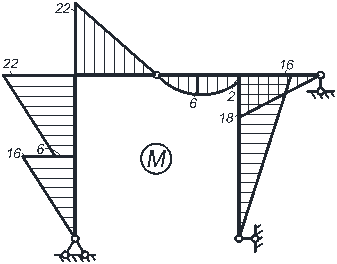
После определения значений усилий, строим эпюры M, Q, N (рис. 4.4). При этом необходимо выполнить проверку выполнения общих закономерностей изменения эпюр.
Для статической проверки составим три уравнения равновесия рамы, подставив полученные значения опорных реакций:
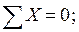
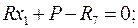
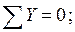
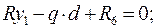
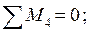
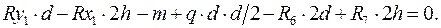
Расчеты произведем в системе компьютерной алгебры MathCAD.
Лабораторная работа № 5
Деформированный вид арки
Цель работы: определить перемещения точек трехшарнирной арки с использованием численного способа вычисления интегралов и получение ее деформированного вида.
Порядок выполнения работы:
1) разбить пролет арки на заданное число частей, определить расчетные сечения;
2) определить перемещения расчетных сечений арки, выполнив расчет по формуле Мора с учетом только изгибающих моментов и используя для численного суммирования формулу трапеций;
3) представить деформированный вид арки;
4) для трех наиболее нагруженных сечений определить перемещения, используя способ левых прямоугольников; сравнить полученные перемещения с результатами, полученными с помощью формулы трапеций.
Все расчеты и построения выполнить в системе компьютерной алгебры MathCAD.
Пример расчета. Для примера рассмотрим расчет арки, рассмотренной ранее в лабораторных работах № 5 и № 6.
Для получения наглядного представления деформированного вида арки, находящейся под действием внешней нагрузки, необходимо знать значения перемещений в каждом сечении арки.
Перемещение k-го сечения арки без учета поперечных и продольных сил определяется по формуле Мора вида:
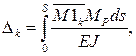
где: S – длина оси арки; 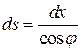 – элементарная длина дуги арки;
– элементарная длина дуги арки;
EJ – жесткость арки при изгибе; 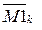 – зависимость изменения единичной эпюры изгибающих моментов от действия единичной сосредоточенной нагрузки, приложенной в k-ом сечении; МР – зависимость изменения эпюры М в арке от действия внешних нагрузок (получена ранее в лабораторной работе № 5).
– зависимость изменения единичной эпюры изгибающих моментов от действия единичной сосредоточенной нагрузки, приложенной в k-ом сечении; МР – зависимость изменения эпюры М в арке от действия внешних нагрузок (получена ранее в лабораторной работе № 5).
Вычисление интегралов мора выполним с использованием численного суммирования по формуле трапеций:
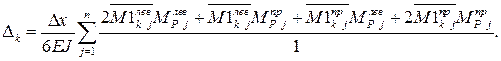
где n – число частей, на которые разбивается пролет арки (в данном случае
n = 16).
Для построения единичных эпюр, рассмотрим арку с приложенной вертикальной единичной сосредоточенной силой F = 1 в k-ом сечении (рис. 6.1).
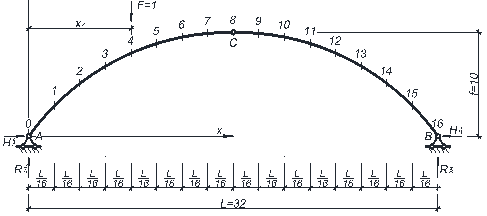
Рисунок 7.1
Опорные реакции в рассматриваемой арке от действия единичной силы:
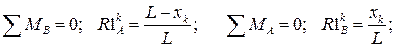
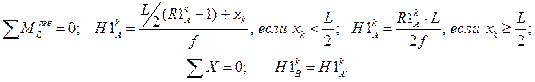
Значения балочных усилий M1o определяются:
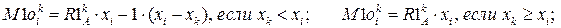
Значения значений единичных эпюр M 1 в сечениях арки определяются:
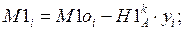
Расчеты выполняем в системе компьютерной алгебры MathCAD. Для построения деформированного вида будем использовать график, наложенный поверх графика очертания арки, подобрав необходимый масштабный коэффициент для отображения перемещений (из-за их малой величины).
Помимо формулы трапеций производить «перемножение» эпюр для определения перемещений можно несколькими другими способами: как более простыми (способом левых прямоугольников, способом правых прямоугольников), так и более точными (по формуле Симпсона).
Например, выберем три сечения, в которых получились наибольшие перемещения (в данном случае – 4, 8, 9), найдем в них перемещения способом левых прямоугольников и убедимся, что этот способ менее точен в сравнении с с формулой трапеций.
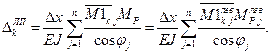
Расхождение результатов, полученных двумя способами: 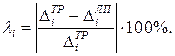
Расчеты произведем в системе компьютерной алгебры MathCAD.
Лабораторная работа № 8
В.И. И гнатюк , Н.В. Бочарова
И 26 Лабораторные работы по дисциплине «Численные методы решения
задач» : методические указания для студентов специальностей 1-70 02 01 «Промышленное и гражданское строительство» и 1-74 04 01 «Сельское строительство и обустройство территорий» дневной и заочной форм обучения. – Брест : Изд-во БрГТУ, 2017. – 47 с.
В методических указаниях представлены лабораторные работы, в которых рассматриваются основы решения численными методами задач расчета строительных конструкций и сооружений с использованием системы компьютерной алгебры MathCAD, включая расчеты с использованием общей системы уравнений равновесия и матриц влияния, использование в расчетах аппроксимаций функций, численного интегрирования, матричной формы определения перемещений, численного дифференцирования, метода конечных разностей, методы решения нелинейных уравнений.
Методические указания предназначены для студентов специальности
1-70 02 01 «Промышленное и гражданское строительство» дневной и заочной форм обучения.
УДК 518:624.04(075)
ББК 38.112
© В.И. Игнатюк, 2017
© Н.В. Бочарова, 2017
© Издательство БрГТУ, 2017
Введение
Численные методы – это методы приближенного решения математических
задач, позволяющие свести решение задачи к выполнению конечного числа
более простых алгебраических и арифметических действий, выполняемых как вручную, так и с помощью компьютерной техники.
В методических указаниях рассматривается применение численных методов к задачам расчета сооружений с использованием методов расчета, которые изучаются в строительной механике.
Для реализации процедур численных методов при решения задач строительства предлагается применять широко распространенный и современный компьютерный пакет прикладной математики MathCAD.
Решение любой практической задачи начинается с математической постановки задачи, включая описание исходных данных, условий и целей на языке математических понятий. Соответственно строится математическая модель.
Математическая модель может иметь вид уравнения, системы уравнений либо быть выраженной в форме математических структур или соотношений. Математические модели могут быть непрерывными или дискретными. После моделирования производится решение математической задачи и исследование математической модели. Процесс исследования свойств объекта по его модели называется моделированием.
В методических указаниях представлены лабораторные работы, в которых рассматриваются расчеты с использованием общей системы уравнений равновесия и матриц влияния, использование в расчетах аппроксимаций функций, численного интегрирования, матричной формы определения перемещений, численного дифференцирования, метода конечных разностей, методы решения нелинейных уравнений. После решения задач численными методами, которые являются приближенными методами, производится при возможности сравнение результатов с точными решениями для оценки полученных результатов и применяемых численных методов расчета.
Основное назначение лабораторных работ – научить студентов применять численные методы в расчетах сооружений, понимать их идеи и суть.
После выполнения лабораторных работ студент по каждой работе оформляет и защищает индивидуальный отчет.
Лабораторные работы соответствуют учебной программой дисциплины «Численные методы решения задач» для студентов специальностей 1-70 02 01 «Промышленное и гражданское строительство» и 1-74 04 01 «Сельское строительство и обустройство территорий», утвержденной 07.07.2015, регистрационный № УД-1-042/уч.
Лабораторная работа № 1
Применение общей системы равновесия строительной механики
к расчету статически определимых ферм
Цель работы: изучить применение общей системы равновесия строительной механики к расчету статически определимых ферм.
Порядок выполнения работы:
1) обозначить приложенную к ферме нагрузку и реакции в опорах;
2) пронумеровать стержни фермы;
3) вырезая каждый узел фермы, составить общую систему равновесия;
4) решить систему уравнений в системе компьютерной алгебры MathCAD;
5) сделать проверку, используя три уравнения равновесия фермы в целом.
Пример расчета. Рассмотрим расчет фермы, представленной на рис. 1.1.
Будем считать, что нагрузка может быть приложена только в узлы верхнего пояса фермы, поэтому обозначим внешнюю нагрузку в виде сосредоточенных сил (P1, P2, P3, P4). Для удобства пронумеруем стержни фермы (1–13).
Обозначим реакции в опорах (RA, RB, HB).
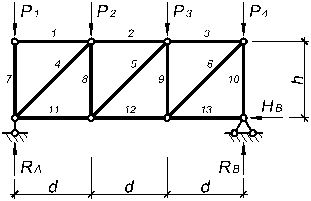
Рисунок 1.1
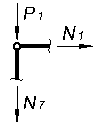
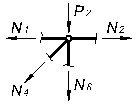
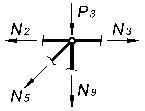
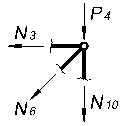
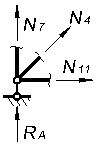
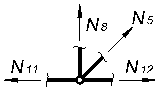
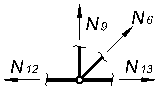
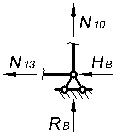
Вырезая каждый узел фермы, обозначим неизвестные продольные усилия стержней фермы (N1, N2, N3, … и т.д., рис. 1.2).
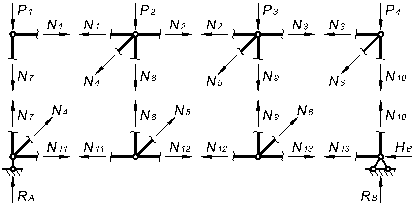
Рисунок 1.2
Составим уравнения равновесия для каждого узла фермы ( 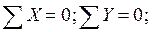 ) проецируя усилия и нагрузки на соответствующие оси.
) проецируя усилия и нагрузки на соответствующие оси.
| 
|
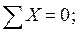 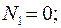
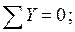 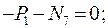
| 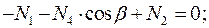
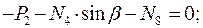
|
| 
|
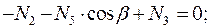
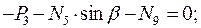
| 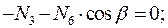
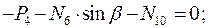
|
| 
|
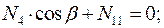
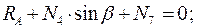
| 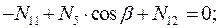
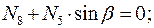
|
| 
|
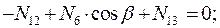
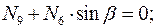
| 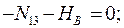
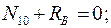
|
Для определения неизвестных усилий и реакций, решим систему уравнений, составленную из полученных ранее уравнений равновесия узлов фермы.
Проверка: 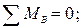
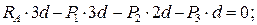
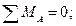
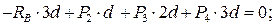
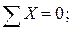
Расчеты произведем в системе компьютерной алгебры MathCAD.
Лабораторная работа № 2
Дата: 2019-02-02, просмотров: 473.