Цель работы: изучить расчет усилий и построение эпюр усилий в двухшарнирный арках с использованием численного подхода.

Порядок выполнения работы:

1) определить опорные реакции и выполнить расчет усилий M, Q, N
в сечениях арки с заданным шагом, обеспечивающим достаточно точное представление нелинейных по длине арки зависимостей усилий;

2) построить для рассматриваемой арки эпюры усилий M, Q, N;

3) выполнить проверку выполнения общих закономерностей изменения эпюр внутренних сил M, Q и N.

Примечание: все необходимые расчеты выполнить в системе компьютерной алгебры MathCAD.

Пример расчета. Выполним расчет двухшарнирной арки с затяжкой представленной на рисунке 8.1.

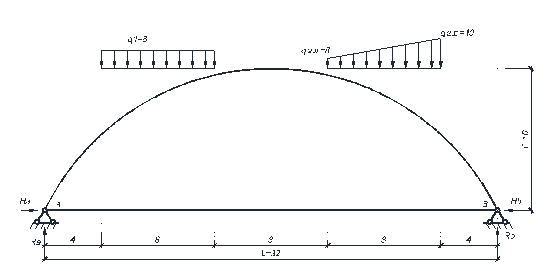
Рисунок 7.1

Жесткость арки принята постоянной по длине стержня  (EJ = Const), жесткость затяжки принята равной EA _зат = 5EJ (k _зат = 5). Ось стержня арки определяется круговой зависимостью, как и в лабораторной работе №4. Основную систему метода сил получим, разрезав затяжку.

Усилия в арке определяем методом сечений. Разбиваем пролет арки на n одинаковых частей ( 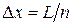), обеспечивающих достаточное число сечений для представления нелинейных по длине арки зависимостей. Отметим, что, чем на большее число частей разобьем пролет, тем меньше будет шаг разбиения Δ х и тем больше будем иметь расчетных сечений для вычисления ординат усилий, и тем более точно можно будет отобразить эпюры усилий.

В данном примере разобьем пролет арки на 16 частей ( 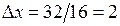 м) и получим 17 расчетных сечений (0, 1, 2, …, 16).

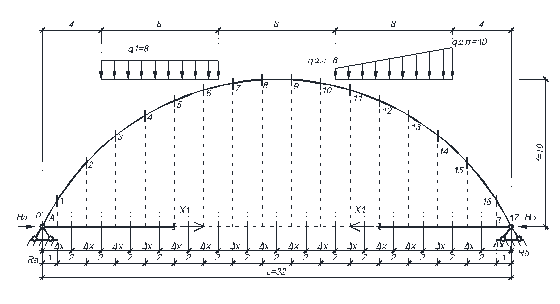
Рисунок 8.2

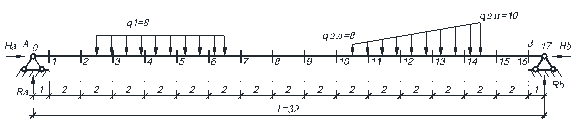
Рисунок 8.3

Расчетные величины (y, sin φ, cos φ, M_P и т.д.) необходимо вычислять в средних точках участков ∆ x, координаты которых можно определить по выражению: x_i = 0,5∆ x + ∆ x (i – 1).

Для арок постоянного сечения жесткости их будут константами и их можно вынести за суммы. Если ввести при этом обозначения:

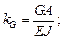
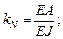
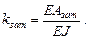
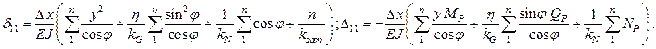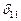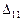 Вычислив перемещения  и , решаем уравнение и находим неизвестное метода сил X₁ = – ∆₁₁ / d₁₁.

После этого можно построить окончательные эпюры изгибающих моментов, поперечных и продольных сил в заданной статически неопределимой арке по формулам:

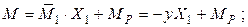
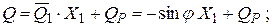
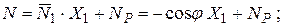
Расчеты произведем в системе компьютерной алгебры MathCAD.

Лабораторная работа № 9

Матричная форма определения перемещений в рамах

Цель работы: изучить применение матричной формы определения перемещений на примере расчета перемещений в раме.

Для выполнения лабораторной работы необходимо:

1) построить грузовую эпюру усилий M_P;

2) в узле, в котором предполагается определить линейное перемещение и угол поворота, приложить единичные усилия в соответствующих направлениях; построить единичные эпюры M ₁ и M ₂;

3) найти искомые перемещения, используя матричную форму; расчеты необходимо произвести в системе компьютерной алгебры MathCAD;

Для примера рассмотрим расчет рамы, рассмотренной в лабораторной работе № 4. Определим горизонтальное перемещение и угол поворота узла 5.

d = 2м;

h = 2м;

P = 4кН;

m = 10кНм;

q = 10кН/м.

Пусть изгибная жесткость

вертикальных стержней равна 4 EJ;

горизонтальных стержней – 2 EJ;

(наклонных стержней – 3 EJ).

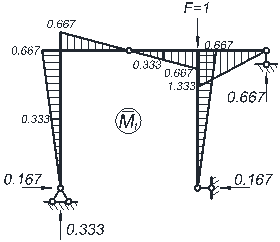
Грузовая эпюра моментов M_P рамы от действия внешней нагрузки была получена ранее.

Составим матрицу-столбец (вектор)
ординат грузовой эпюры M_P:

Примем правило знаков: положительными будем считать значения ординат, находящихся выше или правее стержня.

Для определения вертикального перемещения узла 5 приложим в него единичную сосредоточенную силу F ₁ = 1 вертикально; построим единичную эпюру M ₁ рамы. Соответственно, для определения угла поворота узла 5 приложим в него единичный момент m = 1; построим единичную эпюру M ₂ рамы.

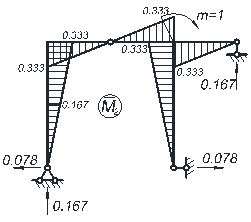
Составим матрицу 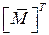, состоящую из двух строк ординат по участкам из единичных эпюр  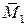и :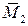

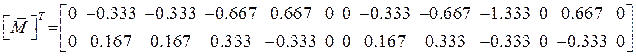
Составим квазидиагональную матрицу упругой податливости системы 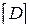, которая состоит из матриц упругой податливости участков  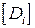и нулевых матриц :

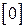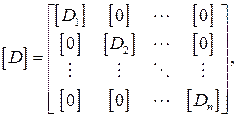
где n – количество участков в системе (в данном примере n = 6).

Составим матрицы упругой податливости участков 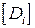 с учетом их длин и изгибных жесткостей, приводя к общему множителю:

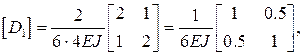
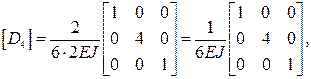
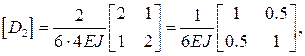
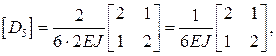
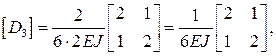
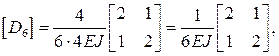
Определим искомые перемещения, используя матричную форму определения перемещений:

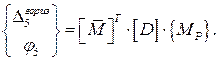
Определим искомые перемещения, произведя расчеты в системе компьютерной алгебры MathCAD:

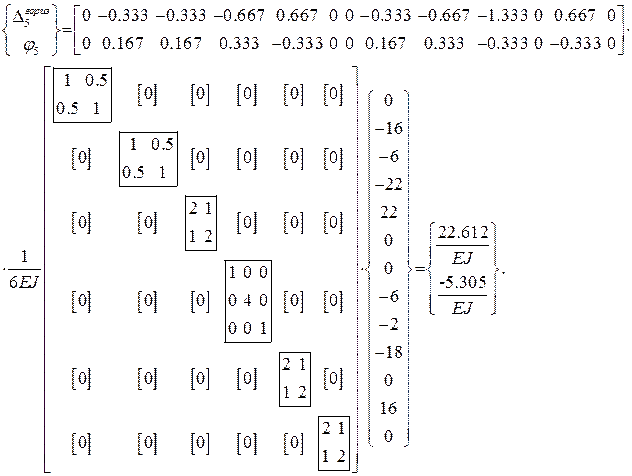
Как видно, в результате нагружения рамы сечение 5 сместилось вниз на 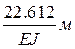, угол поворота этого сечения составил  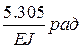против часовой стрелки.

Расчеты произведем в системе компьютерной алгебры MathCAD .

Лабораторная работа № 10