Цель работы: изучить расчет усилий и построение эпюр усилий в трехшарнирных арках с использованием численного подхода.

Порядок выполнения работы:

1) определить опорные реакции и выполнить расчет усилий M, Q, N
в сечениях арки с заданным шагом, обеспечивающим достаточно точное представление нелинейных по длине арки зависимостей усилий;

2) построить для рассматриваемой арки эпюры усилий M, Q, N;

3) выполнить проверку выполнения общих закономерностей изменения эпюр внутренних сил M, Q и N.

Примечание: все необходимые расчеты выполнить в системе компьютерной алгебры MathCAD.

Пример расчета . Рассмотрим расчет арки пролетом L = 32 м со стрелой подъема f = 10 м, ось которой изменяется по круговому закону (рисунок 5.1).

Рисунок 5.1

Определим опорные реакции арки, используя уравнения равновесия:

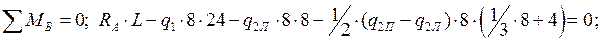
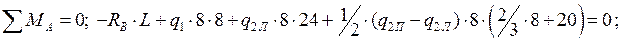
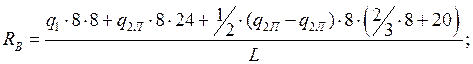
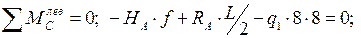
Так как арка нагружена только вертикальными нагрузками, горизонтальные реакции опор будут одинаковы: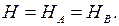

Проверка нахождения реакций опор:

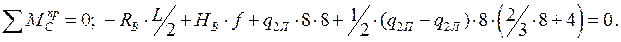
Усилия в арке определяем методом сечений. Разбиваем пролет арки на n одинаковых частей ( 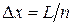), обеспечивающих достаточное число сечений для представления нелинейных по длине арки зависимостей. Отметим, что, чем на большее число частей разобьем пролет, тем меньше будет шаг разбиения Δ х и тем больше будем иметь расчетных сечений для вычисления ординат усилий, и тем более точно можно будет отобразить эпюры усилий.

В данном примере разобьем пролет арки на 16 частей ( 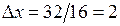 м) и получим 17 расчетных сечений (0, 1, 2, …, 16).

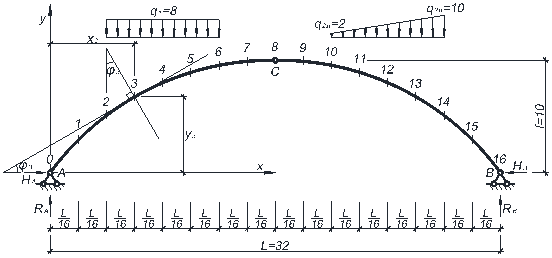
Рисунок 5.2

Рисунок 5.3

Величины усилий M, Q, N в сечениях арки определяются по формулам: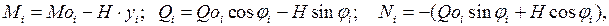

где: Mo_i, Qo_i – изгибающий момент и поперечная сила в i -ом сечении простой двухопорной балки, имеющей такой же пролет, как арка, и нагруженной такой же нагрузкой, как арка (рисунок 5.3); Н – распор арки; y_i, sinφ_i, cosφ_i – ордината, синус и косинус угла наклона касательной к оси арки по отношению к горизонтальной оси (либо угол между нормалью к оси арки и вертикальной осью) для i -го сечения арки (рисунок 5.1).

Абсцисса x_i для каждого (i -го) сечения определяется выражением:

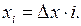
Ординаты y_i, синусы и косинусы углов наклона касательных (sinφ_i, cosφ_i) для сечений найдем, используя геометрические зависимости, представленные для различных очертаний осей арок в приложении к данному разделу.

Все расчеты для сечений и построения эпюр усилий выполняем в системе компьютерной алгебрыMathCAD.

Геометрические характеристики трехшарнирных арок:

а) для круговых арок:

;                   ;

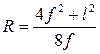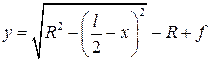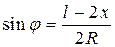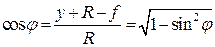;       ;       (5.1)

б) для параболических арок:

;     ;

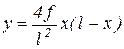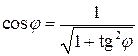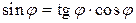; ;                     (5.2)

в) для синусоидальных арок:

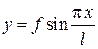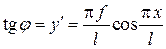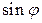; ;  и 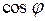 ® см. (4.2);   (5.3)

г) для эллиптических арок:

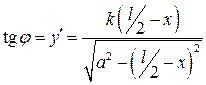;    ;      (5.4)

где: 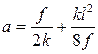   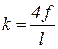 ;  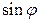 ;        и 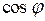  ® см. (5.2);

д) для гиперболических арок:

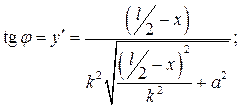              (5.5)

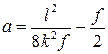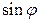где: ;   ;   и 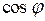  ® см. (5.2).

Лабораторная работа № 6