Цель работы: изучить процедуру определения перемещений в трехшарнирных арках с использованием численного интегрирования.

Порядок выполнения работы:

1) определить перемещение одного из сечений арки, используя формулу Мора и один из численных способов вычисления интегралов, для чего:

1.1) построить эпюры изгибающих моментов, поперечных и продольных сил от действия внешней нагрузки, от которой определяется перемещение;

1.2) в точке (в сечении), перемещение которой определяется, в направлении искомого перемещения приложить единичную «силу» и от ее действия построить единичные эпюры изгибающих моментов, поперечных и продольных сил;

1.3) вычислить перемещение по формуле Мора, используя для вычисления интегралов один из численных способов (например, формулу трапеций).

2) исследовать влияние изгибающих моментов, поперечных и продольных сил на величину перемещения сечения арки, определив вклад в перемещение учета каждой из внутренних сил.

Примечание: все необходимые расчеты выполнить в системе компьютерной алгебры MathCAD.

Пример расчета. Выполним расчет трехшарнирной арки, рассмотренной ранее в лабораторной работе № 4, что позволяет воспользоваться ее результатами, то есть эпюрами М_Р, Q_P, N_P. Определим вертикальное перемещение, например, 4-го сечения (рис 6.1), в котором изгибающий момент от действия внешней нагрузки достигает наибольшей величины.

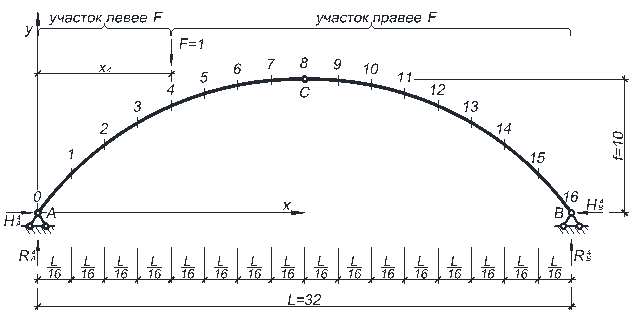
Рисунок 6.1

Перемещение некоторого (i-го) сечения арки в общем случае (с учетом поперечных и продольных сил) определяется по формуле Мора вида

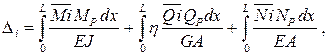
где: EJ, GA, EA – жесткости арки соответственно при изгибе, сдвиге и растяжении-сжатии;

h – коэффициент, учитывающий неравномерность распределения касательных напряжений по высоте сечения при изгибе (для прямоугольного сечения равен 1,2);

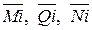 – законы изменения единичных эпюр изгибающих моментов, поперечных и продольных сил в арке от действия единичной сосредоточенной нагрузки, приложенной в i-ом сечении, в котором определяется перемещение;

М_Р, Q_P, N_P – законы изменения эпюр М, Q и N в арке от действия внешних нагрузок (были получены ранее в лабораторной работе № 5).

При замене для вычисления интегралов Мора интегрирования численным суммированием, получим:

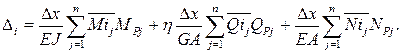
Разбили арку на 16 частей и хотим определить в 4-ом сечении, то выражение примет вид:

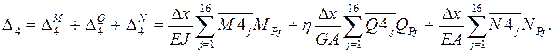
Численное вычисление будем производить по формуле трапеций.

Для построения единичных эпюр рассмотрим арку с приложенной единичной сосредоточенной силой F = 1 в 4-ом сечении (рис. 5.1).

Определим опорные реакции в такой арке:

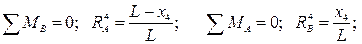
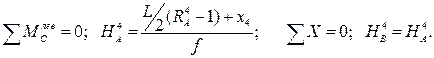
Так как эпюра изгибающих моментов в точке приложения силы F=1 будет иметь излом, а эпюры поперечных и продольных сил будут иметь скачок, то зависимости изменения эпюр этих усилий слева и справа от силы будут различными, и далее в расчете необходимо рассматривать два участка арки (левее и правее единичной силы F). Соответственно будем рассматривать два массива сечений: iL (с 0-го сечения по 4-ое включительно) и iR (с 4-го сечения по 16-е включительно). Значения балочных усилий Mo и Qo определяются:

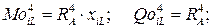(для сечений левее единичной нагрузки),

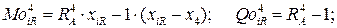(правее единичной нагрузки).

Значения усилий M, Q, N в сечениях арки определяются соответственно:

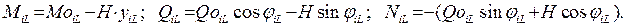
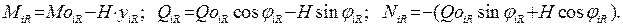
Слагаемые 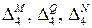 будут определяться как сумма слагаемых выражения перемещения для правого и левого участка арки:

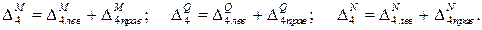
Для исследования влияния усилий M, Q, N на перемещение сечения определим вклад каждого слагаемого выражения перемещения в общую сумму:

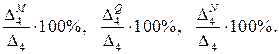
Выполнив расчеты в системе компьютерной алгебры MathCAD, и проанализировав результаты, можно сделать следующий вывод:

наибольшее влияние на величину перемещения оказывают изгибающие моменты, влияние поперечных и продольных сил составляет 3,7%, то есть
невелико, а влияние поперечных составляет 0,435%, то есть незначительно.

Расчеты произведем в системе компьютерной алгебры MathCAD .

Лабораторная работа № 7

Деформированный вид арки

Цель работы: определить перемещения точек трехшарнирной арки с использованием численного способа вычисления интегралов и получение ее деформированного вида.

Порядок выполнения работы:

1) разбить пролет арки на заданное число частей, определить расчетные сечения;

2) определить перемещения расчетных сечений арки, выполнив расчет по формуле Мора с учетом только изгибающих моментов и используя для численного суммирования формулу трапеций;

3) представить деформированный вид арки;

4) для трех наиболее нагруженных сечений определить перемещения, используя способ левых прямоугольников; сравнить полученные перемещения с результатами, полученными с помощью формулы трапеций.

Все расчеты и построения выполнить в системе компьютерной алгебры MathCAD.

Пример расчета. Для примера рассмотрим расчет арки, рассмотренной ранее в лабораторных работах № 5 и № 6.

Для получения наглядного представления деформированного вида арки, находящейся под действием внешней нагрузки, необходимо знать значения перемещений в каждом сечении арки.

Перемещение k-го сечения арки без учета поперечных и продольных сил определяется по формуле Мора вида:

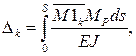
где:  S – длина оси арки; 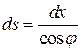 – элементарная длина дуги арки;
EJ – жесткость арки при изгибе; 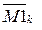 – зависимость изменения единичной эпюры изгибающих моментов от действия единичной сосредоточенной нагрузки, приложенной в k-ом сечении; М_Р  – зависимость изменения эпюры М в арке от действия внешних нагрузок (получена ранее в лабораторной работе № 5).

Вычисление интегралов мора выполним с использованием численного суммирования по формуле трапеций:

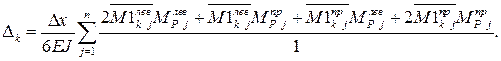
где n – число частей, на которые разбивается пролет арки (в данном случае
n = 16).

Для построения единичных эпюр, рассмотрим арку с приложенной вертикальной единичной сосредоточенной силой F = 1  в k-ом сечении (рис. 6.1).

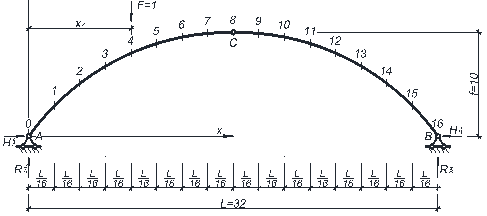
Рисунок 7.1

Опорные реакции в рассматриваемой арке от действия единичной силы:

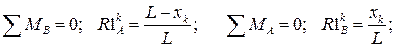
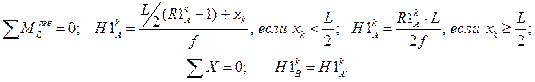
Значения балочных усилий M1o определяются:

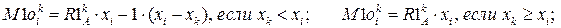
Значения значений единичных эпюр M 1 в сечениях арки определяются:

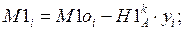
Расчеты выполняем в системе компьютерной алгебры MathCAD. Для построения деформированного вида будем использовать график, наложенный поверх графика очертания арки, подобрав необходимый масштабный коэффициент для отображения перемещений (из-за их малой величины).

Помимо формулы трапеций производить «перемножение» эпюр для определения перемещений можно несколькими другими способами: как более простыми (способом левых прямоугольников, способом правых прямоугольников), так и более точными (по формуле Симпсона).

Например, выберем три сечения, в которых получились наибольшие перемещения (в данном случае – 4, 8, 9), найдем в них перемещения способом левых прямоугольников и убедимся, что этот способ менее точен в сравнении с с формулой трапеций.

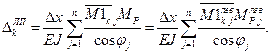
Расхождение результатов, полученных двумя способами: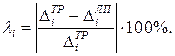

Расчеты произведем в системе компьютерной алгебры MathCAD.

Лабораторная работа № 8