1. −42.
2. { 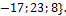
3. в).
4. б); в); г).
5. а); б).
6. а).
7. 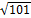 .
.
8. 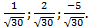
9. 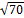 .
.
10. 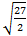 .
.
11. 4.
12. в).
13. в).
14. в).
15. с = − 6а + 4b.
16. а).
II. Элементы линейной алгебры
1. в).
2. б).
3. а), б), в), г).
4. б).
5. г).
6. 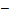 12.
12.
7. а5; б3; в2; г4; д7; е1; ж6.
8. а3; б2; в1.
9. Cистема совместна.
10. АС; ВС; СД; ДВ; СВ.
11.  .
.
12. 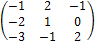 .
.
13. 2.
14.  .
.
15. 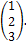
16. г).
III. Аналитическая геометрия
1. а3; б4; в2; г1.
2. а) перпендикулярны; б) пересекаются; в) пересекаются; г) перпендикулярны; д) параллельны.
3. {− 4; 
4. а2; б5; в4; г6; д1; е3.
5. 49.
6. {4;2;−11}.
7. 16x – 6y – z −17= 0.
8.  .
.
9.  .
.
10.  .
.
11. а) параболоид эллиптический; б) гиперболоид однополостный; в) эллипсоид; г) цилиндр эллиптический; д) параболоид гиперболический; е) цилиндр параболический; ж) гиперболоид двуполостный.
12. а) правая ветвь параболы; б) нижняя ветвь гиперболы;
в) нижняя ветвь параболы; г) левая половина эллипса.
13. y2 = 4x.
14. а) 3; 4; F1(0;− 5); F2(0;5); ε =  ; б) 5; 3; F1(− 4; 0); F2(4; 0); ε =
; б) 5; 3; F1(− 4; 0); F2(4; 0); ε =  .
.
15. а) эллипс; б) парабола; в) гипербола; г) прямая.
IV. Введение в анализ
1. а); в).
2. а) [ 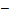 2;2]; б) [0;4]; в) (−∞;0)
2;2]; б) [0;4]; в) (−∞;0) 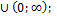 г) (
г) (  ;
; 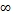 ).
).
3. а) 2; б) 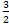 ; г)
; г)  ; в) 0; д)
; в) 0; д)  ; е) 8; ж) 2; з) e8.
; е) 8; ж) 2; з) e8.
4. а); в).
5. а) функция непрерывна; б) х = –2; х = –3 - точки разрыва II рода;
в) x = 4 – точка разрыва II рода.
6. а); г).
7. а1; б1; в1; г4; д2; е1; ж5; з1; и6; к1; л3.
8. а)  ; б) 3; в)
; б) 3; в)  ; г)
; г) 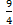 .
.
V. Дифференциальное исчисление функций одной переменной
1. а) 24x 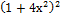 ; б) sin 2x; в) arcsin (ln x) +
; б) sin 2x; в) arcsin (ln x) + 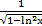 ;
;
г) 2x e−2x(1 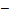 x); д)
x); д) 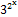 ln3 2x ln2 ;
ln3 2x ln2 ;
е) 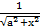 ; ж) xsin x(cos x ln x +
; ж) xsin x(cos x ln x + 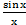 ); з) 2xlnx−1lnx;
); з) 2xlnx−1lnx;
и) 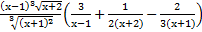 ; к)
; к) 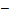 1,5 ctg t; л)
1,5 ctg t; л) 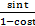 ;
;
м) 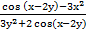 ; н)
; н) 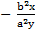 ;
;
2. а7; б5; в9; г8; д10; е1; ж3; з6; и2; к4.
3. б).
4. а).
5. а) 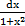 ; б)
; б) 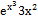 dx.
dx.
6. а) 4,9; б) 0,02, в) 1,035.
7. а) 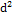 y = 4e2x dx2; б ) dy2 = −
y = 4e2x dx2; б ) dy2 = − 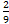
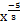 dx2.
dx2.
8. (–2; –  ); (2;
); (2;  ).
).
9. а) 1; б) 9; в)  ; г) 2.
; г) 2.
10. а) sin (x + 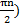 ; б)
; б) 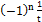 .
.
VI. Исследование функций и построение графиков
1. а4; б1; в3; г2.
2. y = 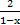 .
.
3. а); б); д).
4. а).
5. г).
6. а); в).
7. (0; 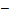 2).
2).
8. в точке х = 4, ymin = − e4.
9. Наименьшее y = −10, наибольшее y = 2,25.
10. 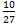 .
.
VII. Комплексные числа
1. а2; б3; в1ю.
2. б) ю.
3. а) 3+ i; б) 4 + 3i; в) i.
4. 215.
VIII. Интегральное исчисление функций одной переменной
1. а6; б5; в9; г7; д3; е1; ж10; з2; и12; к8; л4; м11; н13.
2.
а)  arctg arctg  + C; + C;
| и) 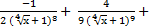 C; C;
|
б) 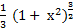 + C; + C;
| к) 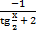 + C; + C;
|
в) 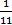 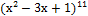 + C; + C;
| л) 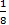 x - x - 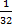 sin 4x + C; sin 4x + C;
|
г) −  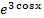 + C; + C;
| м) 2 ln 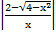 + + 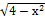 + C; + C;
|
д) – 3cos 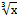 + C; + C;
| н)  ; ;
|
| е) – x cos x +sin x + C; | о)  ; ;
|
ж) 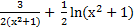 + C; + C;
| п) 0; |
з) − 3 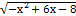 + 13 arcsin (x + 13 arcsin (x  3) + C; 3) + C;
| р)  −1. −1.
|
3. Подынтегральная функция – нечетная.
4. а); б); г); д); е).
5. 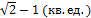 .
.
6. а) сходится , 1; б) сходится, π; в) расходится; г) сходится ,  .
.
7. 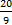 .
.
8.  (2
(2 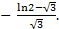
9. 0,3π (куб.ед.)
10. 0 ≤ 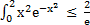 .
.
IX. Дифференциальное исчисление функций нескольких переменных
1. а) x2 + y2 ≥ 1 – часть плоскости вне единичного круга:
б) полоса между параллельными прямыми x + y ≤ 1 и x + y≥ − 1;
в) полуплоскость x ≥ 0.
2. а) 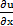 = 2x – 3y − 4;
= 2x – 3y − 4; 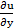 = 4y − 3x + 2.
= 4y − 3x + 2.
б) 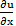 =
= 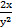 −
− 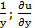 =
= 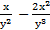 .
.
в) 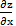 =
= 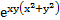 3x2y + y3;
3x2y + y3; 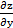 =
= 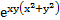 (x3+ 3xy2).
(x3+ 3xy2).
г)  =
= 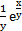 ;
; 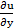 = −
= − 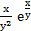 +
+ 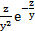 ;
; 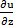 = −
= − 
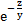 .
.
д) 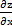 =
= 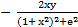 ;
; 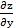 =
= 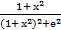 .
.
3. dz =  .
.
4. 0.
5. Касательная плоскость x − 2y + z = 0; нормаль 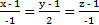 .
.
6. 3,02.
7. в).
8. zmin = − 9.
9. zнаим = 5; zнаиб = 11.
X. Кратные интегралы
1. а) 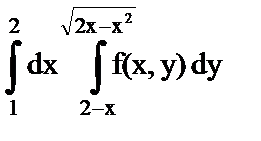 ;
;
б) 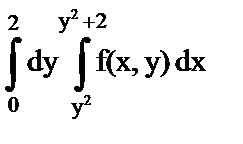

2. а) 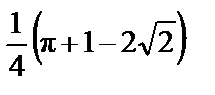 ; б) 26.
; б) 26.
3. б).
4. а) 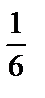 (кв.ед.); б)
(кв.ед.); б) 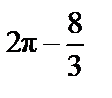 (кв.ед.); в)
(кв.ед.); в) 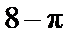 (кв.ед.)
(кв.ед.)
5. а) 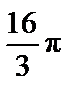 (кв.ед.); б)
(кв.ед.); б) 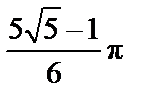 (кв.ед.).
(кв.ед.).
6. а) 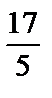 (куб.ед.); б) 90 (куб.ед.).
(куб.ед.); б) 90 (куб.ед.).
7. а4; б3; в1; г6; д2; е5.
8. б).
9. а) 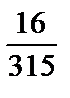 ; б)
; б) 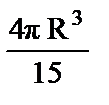 .
.
10. а5; б2; в6; г1; д7; е3; ж4; з8.
11. 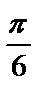 (куб.ед).
(куб.ед).
12. 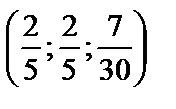 .
.
13. 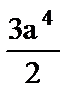 .
.
XI. Дифференциальные уравнения
1. б).
2. б).
3. а).
4. а4, б9, в11, г1, д8, е2, ж10, з3, и5, к7, л6.
5. а)  ;
;
б) 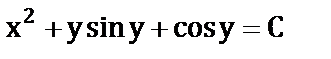 ;
;
в) 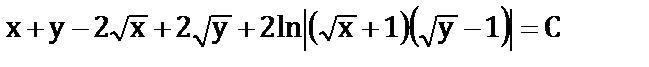 ;
;
г) arctg 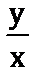
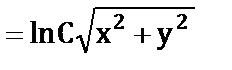 ;
;
д) 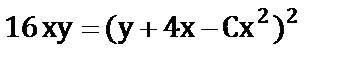 ;
;
е) 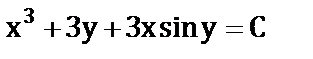 ;
;
ж)  ;
;
з) 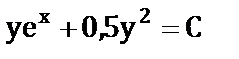 ;
;
и) 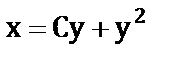 ;
;
к) 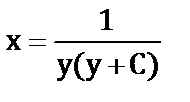 .
.
6. а) 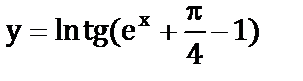 ;
;
б) 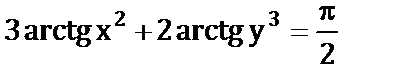 ;
;
в) 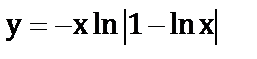 ;
;
г) 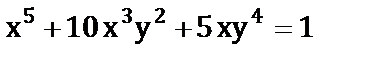 ;
;
д) 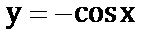 ;
;
е) 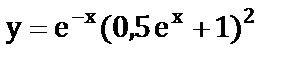 ;
;
ж) 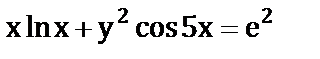 ;
;
з) 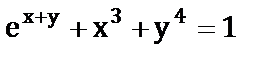 .
.
7. а)  ;
;
б) 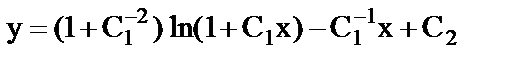 ;
;
в)  .
.
8. а) 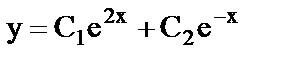 ;
;
б) 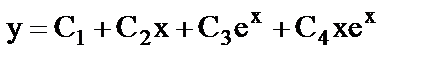 ;
;
в) 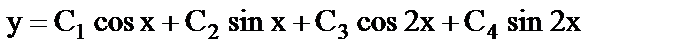 .
.
9. а) 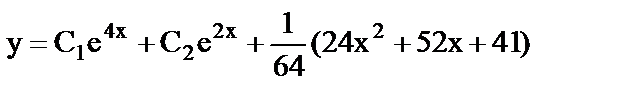 ;
;
б)  ;
;
в) 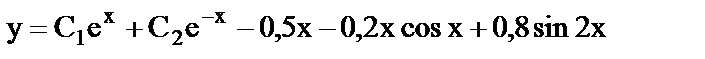 ;
;
г)  .
.
10. б), в).
11. а) 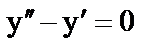 ; б)
; б) 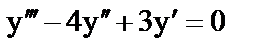 .
.
12. а) нет; б) да.
13. а) 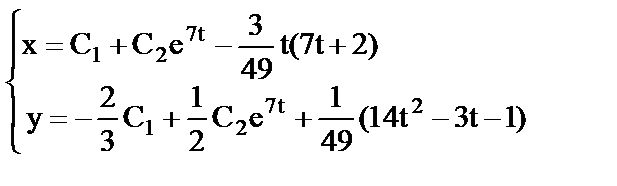 ;
;
б) 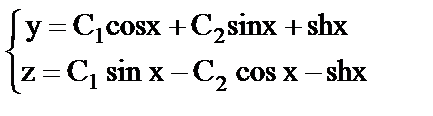 .
.
XII. Ряды
1. а) 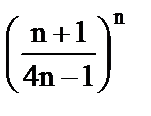 ; б)
; б) 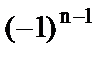 .
.
2. а) 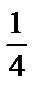 ; б)
; б) 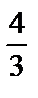 .
.
3. а1; б1; в3; г1, д1;е2.
4. а) расходится; 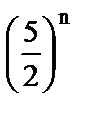 ; б) сходится;
; б) сходится; 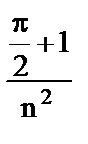 .
.
5. а) расходится; 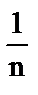 ; б) расходится;
; б) расходится; 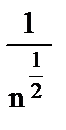 ; в) расходится;
; в) расходится; 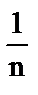 .
.
6. а) расходится, (первый признак сравнения);
б) сходится, (второй признак сравнения);
в) расходится, ( признак Даламбера);
г) сходится, (признак Коши);
д) сходится, (интегральный признак).
7. а) сходится условно;
б) сходится абсолютно;
в) расходится.
8. а5; б4; в2; г1; д3.
9. б).
10. а) 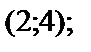 б)
б) 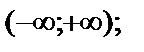 в)
в) 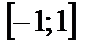 .
.
11. а) нет; б) нет; в) нет; г) да; д) да.
12. 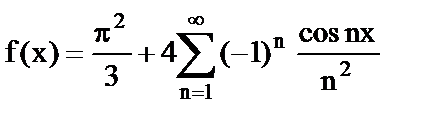 .
.
13. 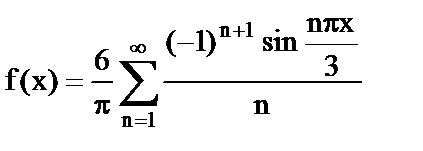 .
.
Список литературы
1. Берман Г. Н. Сборник задач по курсу математического анализа. – CПб.: Профессия, 2006.
2. Выгодский М. Я. Справочник по высшей математике. – М.: Наука, 1977.
3. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч 1: Учеб. пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Мир и образование, 2007.
4. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч 2: Учеб. пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Мир и образование, 2007.
5. Клетеник Д. В. Сборник задач по аналитической геометрии: Уч.пособие для втузов. – 17 изд. –СПб.: Профессия, 2005.
6. Лунгу К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 3-е изд. – М.: Айрис-пресс, 2003.
7. Лунгу К. Н. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу, В. П. Норин, Д. Т. Письменный, Ю. А. Шевченко, Е. Д. Кулагин. – 4-е изд. – М.: Айрис-пресс, 2006.
8. Письменный Д. Т. Конспект лекций по высшей математике: Полный курс. – 2-е изд. – М.: Айрис-пресс, 2004.
9. Сборник задач по математике для втузов. Ч. 1/ под ред. А. В. Ефимова, Б. П. Демидовича. – М.: Наука, 1986.
Составитель Н.А. Смирнова
Задания по математике
в тестовой форме
для организации самостоятельной работы
Учебно-методическое пособие
для студентов
Дата: 2019-02-02, просмотров: 328.