1. Выбрать правильный ответ.
Дифференциальное уравнение ‒ это
а) уравнение, связывающее функцию, дифференциал функции и дифференциал независимой переменной;
б) уравнение, связывающее независимую переменную,функцию и производные этой функции;
в) уравнение, связывающее независимые переменные, их функцию и первообразные функции;
г) уравнение, связывающее независимые переменные, их функцию, производные и первообразные этой функции.
2. Выбрать правильный ответ.
Всякое решение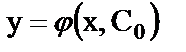 
, получившееся из общего решения, называется:
а) решением дифференциального уравнения;
б) частным решением дифференциального уравнения;
в) особым решением дифференциального уравнения.
3. Выбрать правильный ответ.
Дифференцируемая функция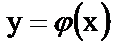 
, которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество
называется:
а) решением дифференциального уравнения;
б) общим решением дифференциального уравнения;
в) частным решением дифференциального уравнения;
г) особым решением дифференциального уравнения.
4. Установить правильное соответствие.
а)  ;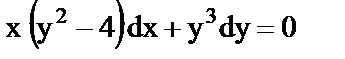
| 1) линейное относительно y и y' дифференциальное урав- нение; |
б)  ;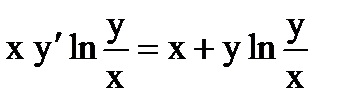
| 2) линейное однородное дифференциальное уравнение с постоянными коэффициен- тами; |
в)  ;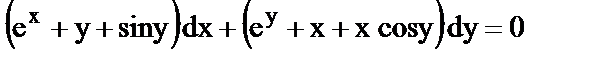
| 3) линейное однородное дифференциальное уравнение второго порядка; |
г)  ;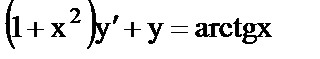
| 4) дифференциальное уравнение с разделяющимися переменными; |
д)  ;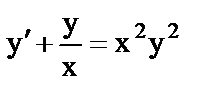
| 5) дифференциальное уравнение третьего порядка; |
е)  ;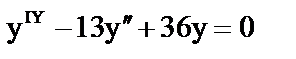
| 6) линейное относительно x и x' дифференциальное уравнение; |
ж)  ;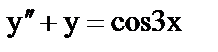
| 7) дифференциальное уравнение, приводящееся к однородному; |
з)  ;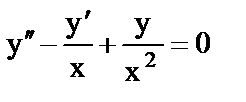
| 8) уравнение Бернулли; |
и)  ;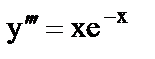
| 9) однородное дифференциальное уравнение первого порядка; |
к)  ;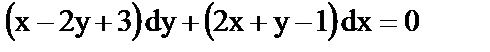
| 10) линейное неоднородное дифференциальное уравнение с постоянными коэффициентами; |
л)  .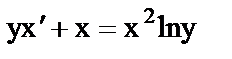
| 11) Дифференциальное уравнение в полных дифференциалах. |
5. Решить уравнения:
а)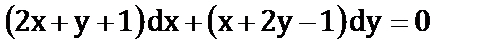 
;
б)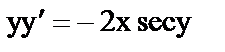 
;
в)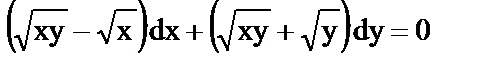 
;
г)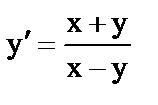 
;
д)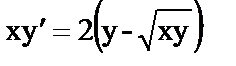 
;
е)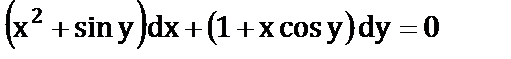 
;
ж)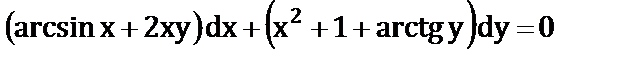 
;
з)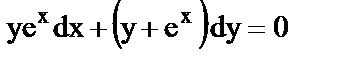 
;
и)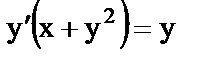 
;
к)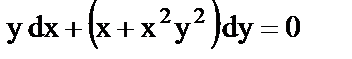 
.
6. Решить задачу Коши:
а)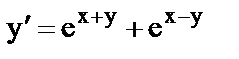 
; 
;
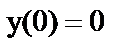б)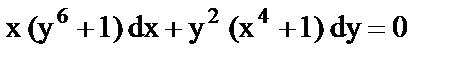 
; 
;
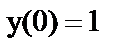в)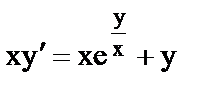 
; 
;
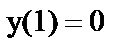г)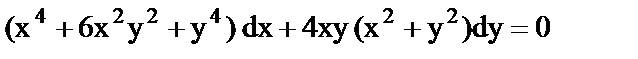 
; 
;
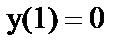д)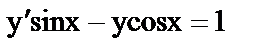 
; 
;
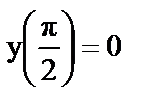е)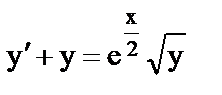 
; 
;
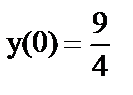ж)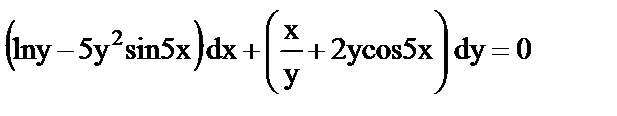 
; 
;
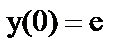з)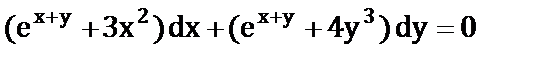 
; 
.
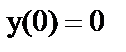7. Решить уравнения
а)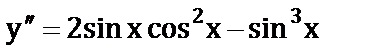 
;
б)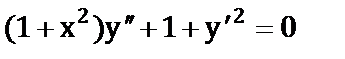 
;
в)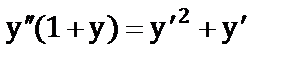 
.
8. Найти общие решения уравнений
а)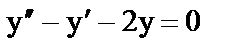 
;
б)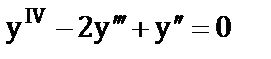 
;
в)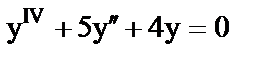 
.
9. Решить уравнения
а)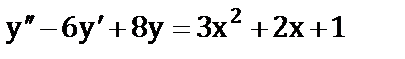 
;
б)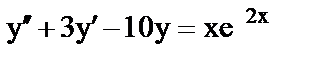 
;
в)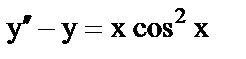 
;
г)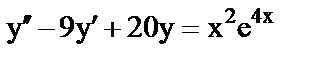 
.
10. Выбрать все правильные ответы.
Для решения линейных неоднородных уравнений n-го порядка со специальной правой частью применяется
а) метод Бернулли;
б) метод вариации произвольных постоянных;
в) метод Лагранжа;
11. Составить линейное однородное дифференциальное уравнение с постоянными коэффициентами, фундаментальная система решений которого имеет вид
а) 1, ex;
б) 1, ex, e3x.
12. Дано дифференциальное уравнение и его частные решения. Составляют ли они фундаментальную систему?
а)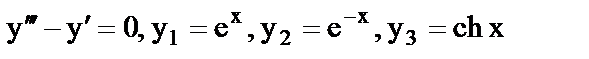 
;
б)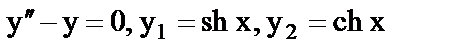 
.
13. Найти решение системы дифференциальных уравнений
а)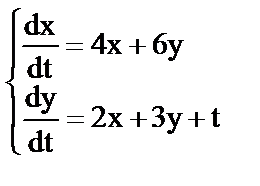 
;
б)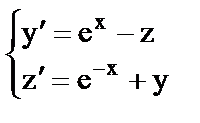 
.
XII. Ряды
1. Найти общий член ряда
а)  ;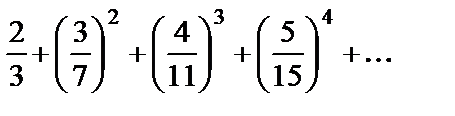
| |
б)  .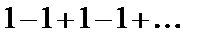
| |
2. Найти сумму ряда
а)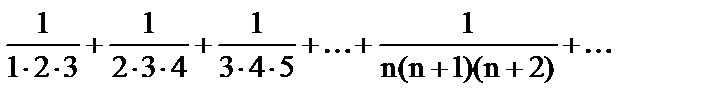 
;
б)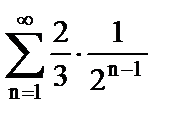 
.
3. Установить правильное соответствие.
| а) признак Даламбера; | 1) достаточный признак сходимости знакоположительного ряда; |
| б) признак сравнения; | |
| в) признак Вейерштрасса; | 2) необходимый признак сходимости знакочередующегося ряда; |
| г) интегральный признак; | |
| д) признак Коши; | 3) достаточный признак равномерной сходимости функционального ряда. |
| е) признак Лейбница. |
4. Исследовать ряд на сходимость. Указать общий член ряда, с которым сравнивается данный ряд
а)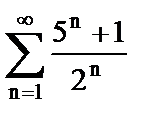 
;
б)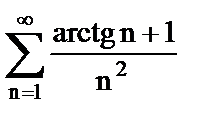 
.
5. Исследовать ряд на сходимость, применяя предельный признак сравнения. Указать общий член ряда, с которым сравнивается данный ряд
а)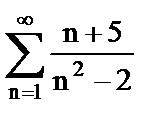 
;
б)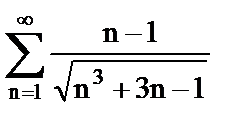 
;
в)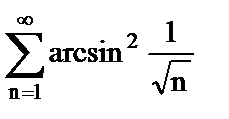 
.
6. Исследовать сходимость рядов
а)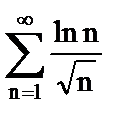 
;
б)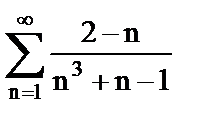 
;
в)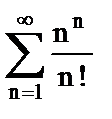 
;
г)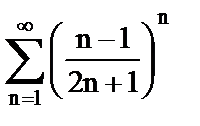 
;
д)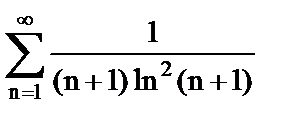 
.
7. Исследовать ряды на сходимость
а)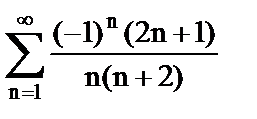 
;
б)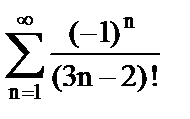 
;
в)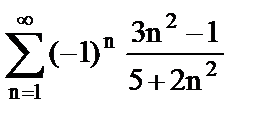 
.
8. Установить правильное соответствие.
| а) |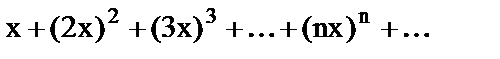 
| 1) | Знакоположительный ряд; |
| б) |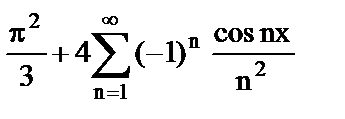 
| 2) | Знакочередующийся ряд; |
| в) |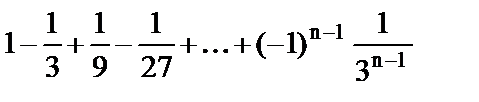 
| 3) | Степенной ряд; |
| г) |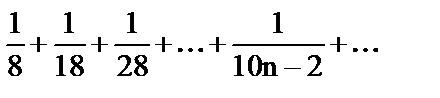 
| 4) | Ряд Фурье; |
| д) |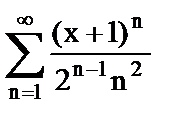 
| 5) | Функциональный ряд. |
9. Выбрать правильный ответ.
Ряд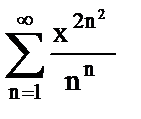 
сходится в точке x0,
а) x0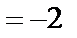 
;
б) x0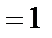 
;
в) x0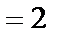 
.
10. Найти область сходимости ряда
а)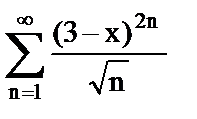 
;
б)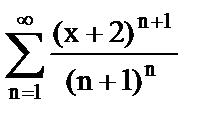 
;
в)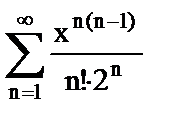 
.
11. Может ли интервал сходимости ряда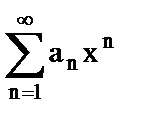 
быть таким
а) (−2;0);
б) (0;2);
в) (−3;1);
г) (−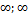 
);
д)(−3;3).
12. Разложить в ряд Фурье функцию f(x)=x2, заданную на интервале
[− 
].
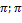13. Разложить в ряд Фурье функцию f(x)=x, заданную на интервале (−3;3).
Ответы
Дата: 2019-02-02, просмотров: 319.
