Составитель: Н. А. Смирнова, старший преподаватель
Кафедры ВМ
Рецензент: Н. В. Ракита, доцент кафедры ВМ
Рекомендовано к изданию на заседании кафедры «ВМ» 22.04.2014г.
Задания по математике в тестовой форме для организации самостоятельной работы: учебно-метод. пособие. - Ижевск: Изд-во ИжГТУ, 2014.- 42с.
Учебно-методическое пособие разработано для использования при самоподготовке студентов к экзамену по дисциплине «Математика». Приведены задания в различных формах: открытой, закрытой и на установление соответствия. В конце издания указаны ответы.
Пособие предназначено для студентов обучающихся по направлению 270800.62 «Строительство» профиль «Промышленное и гражданское строительство» при изучении дисциплин «Математика 1», «Математика 2», «Математика 3».
© Смирнова Н.А., составление, 2014
I. Элементы векторной алгебры
1. Найти скалярное произведение векторов a и b, а ={1; 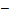 1;5}, b ={3;5;
1;5}, b ={3;5; 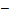 8}.
8}.
2. Найти векторное произведение векторов а и b, а ={1; 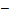 1;5}, b ={3;5;
1;5}, b ={3;5; 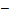 8}.
8}.
3. Выбрать пару коллинеарных векторов:
а) а ={1: 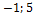 }, b ={
}, b ={ 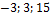 };
};
б) а ={2; 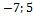 }, b ={2;
}, b ={2; 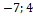 };
};
в) а ={4;6; 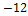 }, b ={
}, b ={ 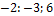 };
};
г) а ={0;1;1}, b ={1;0;0}.
4. Выбрать пару перпендикулярных векторов:
а) а = {1; 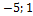 }, b = {3;5;
}, b = {3;5; 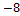 };
};
б) а = {1; 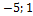 }, b ={4;9;1};
}, b ={4;9;1};
в) а ={0;1;0}, b ={1;0; 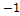 };
};
г) а ={2;7}, b ={ 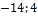 }.
}.
5. Выбрать тройки компланарных векторов:
а) а = {1; 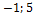 }, b = {3;5;
}, b = {3;5; 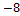 }, с = {1;
}, с = {1; 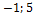 };
};
б) а ={1; 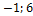 }, b ={
}, b ={  }, с ={1
}, с ={1 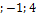 };
};
в) а ={1;2;3}, b ={4;5;6}, с ={7;8;11};
г) а ={1;0;0}, b ={0;1;0}, с ={0;0;1}.
6. Пусть m = 2а + 3b. Тогда, если а = {1; 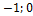 }; b = {2;
}; b = {2; 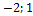 } , то
} , то
а) 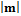 =
= 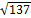 ;
;
б) 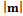 =2;
=2;
в) 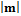 =
= 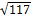 ;
;
г) 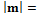 1,5.
1,5.
7. Найти модуль вектора 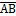 , если А(12;
, если А(12; 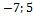 ), В(16;0;
), В(16;0; 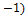 .
.
8. Найти направляющие косинусы для вектора а ={1;2 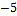 } .
} .
9. Найти площадь параллелограмма, построенного на векторах а и b:
а ={1; 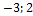 }, b ={2;0;
}, b ={2;0; 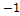 }.
}.
10. Вычислить площадь треугольника АВС, где А(1;2;0), В(3;2;1), С( 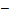 2;1;2).
2;1;2).
11.Вычислить объем пирамиды АВСД, где А(5;1; 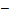 4), В(1;2;
4), В(1;2; 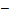 1), С(3;3;
1), С(3;3; 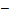 4), Д(2;2;2).
4), Д(2;2;2).
12. Указать левую тройку векторов:
а) а ={ 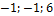 }, b ={
}, b ={  }, с ={1;
}, с ={1; 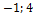 };
};
б) а ={ 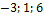 }, b ={
}, b ={ 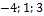 }, с ={
}, с ={ 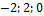 };
};
в) а ={0;3;0}, b ={4;0;0}, с ={0;0;5}.
13. Выбрать утверждение, не соответствующее определению векторного произведения:
а) векторным произведением векторов а и b является вектор с, перпендикулярный векторам а и b;
б) 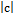 =
= 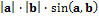 ;
;
в) векторным произведением векторов а и b является вектор с, коллинеарный векторам а и b;
г) векторы а,b,с образуют правую тройку.
14. Орт вектора по определению – это:
а) проекция вектора на ось ОХ;
б) направление вектора;
в) единичный вектор, имеющий одинаковое направление с данным;
г) любой вектор единичной длины.
15. Заданы векторы: а ={1;1;3}, b ={2;2;1}, с ={2;2; 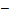 14}.
14}.
Разложить вектор с по базису а, b.
16. Выбрать правильный ответ.
Вектор а ={2;5} повернули на 90° против часовой стрелки, его новые координаты:
а) { 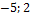 };
};
б) { 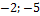 };
};
в) {5; 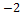 };
};
г) { 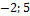 }.
}.
IV. Введение в анализ
1. Выбрать все правильные ответы.
Последовательность 1 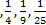
а) ограниченная;
б) неограниченная;
в) бесконечно малая;
г) бесконечно большая.
2. Найти область определения функции:
а) y = 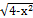 + 1;
+ 1;
б) y = arccos ( 
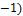 ;
;
в) y = 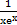 ;
;
г) y = lg (3x−1) + 2 lg (x+1).
3. Вычислить пределы:
a)
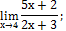
| д)
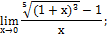
|
б)
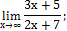
| е)
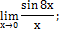
|
в)
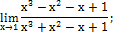
| ж)
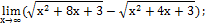
|
г)
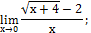
| з)
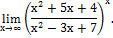
|
4. Выбрать все верные утверждения. Для функции y = arctg 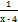 :
:
а) точка x = 4 является точкой разрыва I рода;
б) точка x = 4 является точкой разрыва II рода;
в) скачок функции в точке х = 4 равен π;
г) в точке х = 4 функция непрерывна.
5. Найти точки разрыва функций:
а) у = 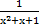 ;
;
б) y = 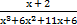 ;
;
в) y = 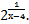
6. Выбрать правильный ответ.
Функция y = 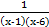 непрерывна на промежутке:
непрерывна на промежутке:
а) (2;5);
б) (4;10);
в) (0;7);
г) (− 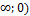 .
.
7. Установить правильное соответствие.
Бесконечно малые эквивалентны (при α→ 0, β→∞):
| а) sin α; | 1) α ; |
| б) tg α; | 2) 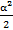 ; ;
|
в) 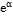 − 1; − 1;
| 3)  ; ;
|
г) 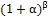 ; ;
| 4) 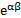 ; ;
|
| д) 1- cos α; | 5) 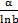 ; ;
|
е) 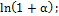
| 6) α 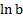 . .
|
ж) 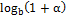 ; ;
| |
| з) arcsin α; | |
и) 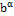 −1; −1;
| |
| к) arctg α. | |
л) 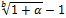 . .
|
8. Вычислить:
a)
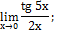
|
б)
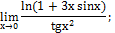
|
в)
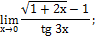
|
г)
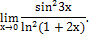
|
VII. Комплексные числа
1. Установить правильное соответствие :
| а) z = x + iy; | 1) тригонометрическая форма; |
| б) z = riφ; | 2) алгебраическая форма; |
| в) z =(cos φ+isin φ). | 3) показательная форма. |
2. На комплексной плоскости число z = −1 + i 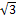 расположено:
расположено:
а) в I четверти;
б) во II четверти;
в) в III четверти;
г) в IV четверти.
3. Для чисел z1 = − 1+2i и z2 = 2− i вычислить:
а) сумму;
б) произведение;
в) частное.
4. Вычислить по формуле Муавра ( 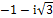 )15.
)15.
X. Кратные интегралы
1. Изменить порядок интегрирования
а) 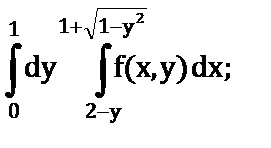
б) 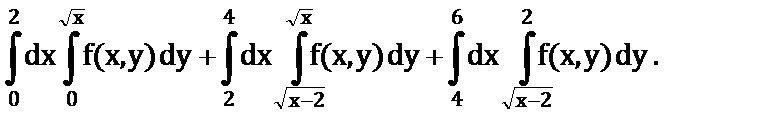
2. Вычислить:
а) 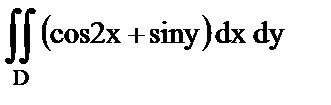 , если область D ограничена линиями
, если область D ограничена линиями 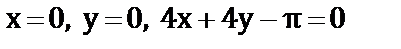 ;
;
б) 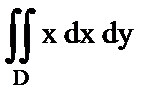 , если D – треугольник с вершинами А(2;3), В(7;2), С(4;5).
, если D – треугольник с вершинами А(2;3), В(7;2), С(4;5).
3. Выбрать правильный ответ.
Якобиан перехода к полярным координатам равен
а) 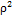 ;
;
б) 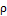 ;
;
в) 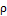 cosφ;
cosφ;
г) 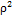 sinφ;
sinφ;
где ρ – полярный радиус, φ – полярный угол.
4. Вычислить площадь фигуры, ограниченной линиями
а) 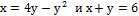 ;
;
б) 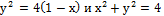 (вне параболы);
(вне параболы);
в) 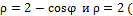 вне кардиоиды).
вне кардиоиды).
5. Вычислить площадь
а) части сферы 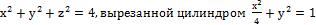 ;
;
б) части поверхности параболоида 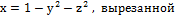
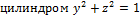 .
.
6. Вычислить объем тел, ограниченных заданными поверхностями
а) 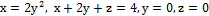 ;
;
б) 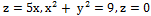 .
.
7. Установить правильное соответствие.
Если γ ‒ поверхностная плотность пластины, D – область плоскости XOY.
| а) Масса плоской пластины; | 1) 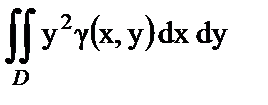 ; ;
|
| б) Статический момент пластины относительно оси OY; | 2) 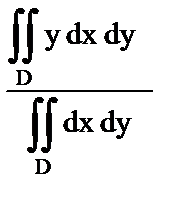 ; ;
|
| в) Момент инерции пластины относительно оси OX; | 3) 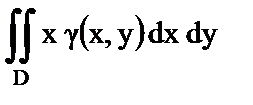  ; ;
|
| г) Момент инерции пластины относительно начала координат; |
4) 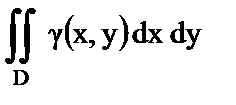 ; ;
|
| д) Ордината центра тяжести однородной пластины; |
5) 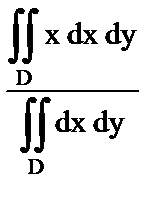 ; ;
|
| е) Абсцисса центра тяжести однородной пластины. |
6) 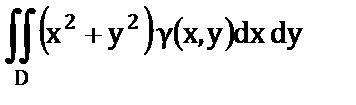 . .
|
8. Выбрать правильный ответ.
Якобиан перехода к сферическим координатам равен
а) 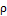 ;
;
б) 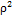 sinθ;
sinθ;
в) 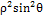 ;
;
г) 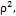
где ρ ‒ полярный радиус, θ ‒ угол между полярным радиусом и осью Оz.
9. Вычислить
а) 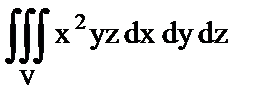 ; если область V ограничена плоскостями
; если область V ограничена плоскостями
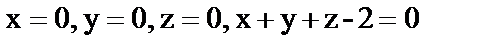 ;
;
б) 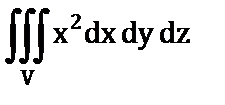 , если V – шар
, если V – шар 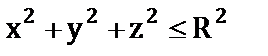 .
.
10. Установить правильное соответствие.
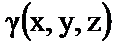 – плотность тела.
– плотность тела.
| а) Объем тела, занимающего область V; | 1) 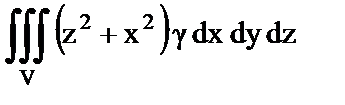 ; ;
|
| б) Масса тела, занимающего область V; | 2) 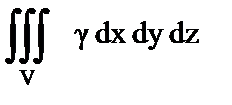 ; ;
|
| в) Апликата центра тяжести тела; | 3) 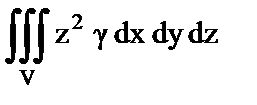 ; ;
|
| г) Момент инерции относительно оси OY; | 4) 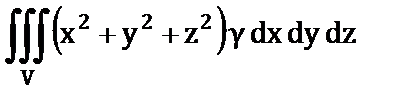 ; ;
|
| д) Абсцисса центра тяжести тела; | 5) 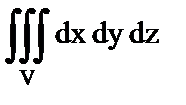 ; ;
|
| е) Момент инерции относительно плоскости XOY; | 6) 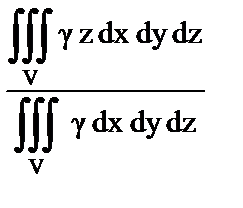 ; ;
|
| ж) Момент инерции относительно начала координат; | 7) 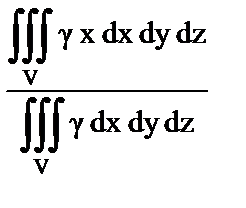 ; ;
|
| з) Статистический момент тела относительно плоскости XOZ. | 8) 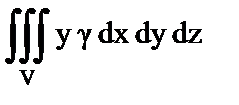 . .
|
11. Вычислить объем тела, ограниченного поверхностями 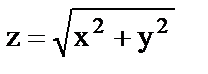 и
и
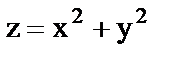 .
.
12. Найти координаты центра тяжести тела, ограниченного поверхностями 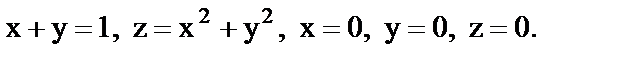
13. Найти массу куба 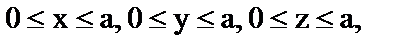 если плотность в точке
если плотность в точке
(x, y, z) есть 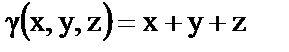 .
.
XII. Ряды
1. Найти общий член ряда
а) 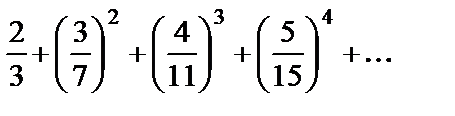 ; ;
| |
б) 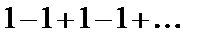 . .
| |
2. Найти сумму ряда
а) 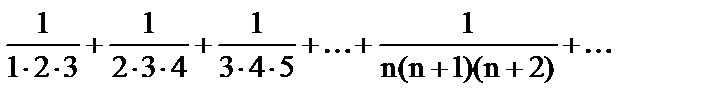 ;
;
б) 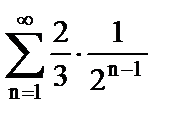 .
.
3. Установить правильное соответствие.
| а) признак Даламбера; | 1) достаточный признак сходимости знакоположительного ряда; |
| б) признак сравнения; | |
| в) признак Вейерштрасса; | 2) необходимый признак сходимости знакочередующегося ряда; |
| г) интегральный признак; | |
| д) признак Коши; | 3) достаточный признак равномерной сходимости функционального ряда. |
| е) признак Лейбница. |
4. Исследовать ряд на сходимость. Указать общий член ряда, с которым сравнивается данный ряд
а) 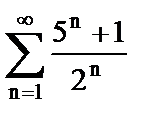 ;
;
б) 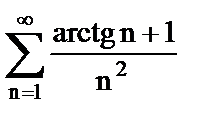 .
.
5. Исследовать ряд на сходимость, применяя предельный признак сравнения. Указать общий член ряда, с которым сравнивается данный ряд
а) 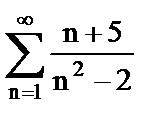 ;
;
б) 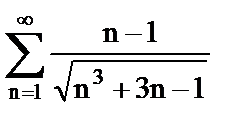 ;
;
в) 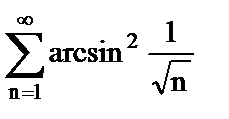 .
.
6. Исследовать сходимость рядов
а) 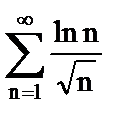 ;
;
б) 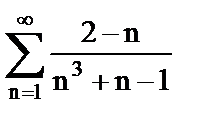 ;
;
в) 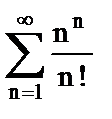 ;
;
г) 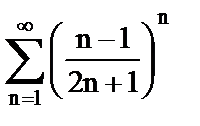 ;
;
д) 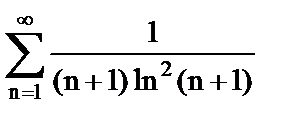 .
.
7. Исследовать ряды на сходимость
а) 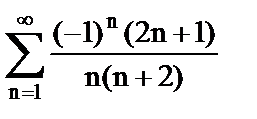 ;
;
б) 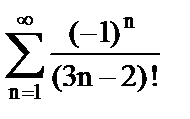 ;
;
в) 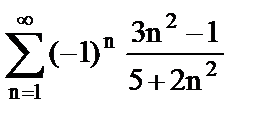 .
.
8. Установить правильное соответствие.
| а) | 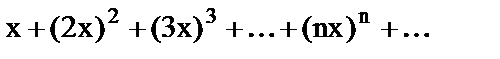
| 1) | Знакоположительный ряд; |
| б) | 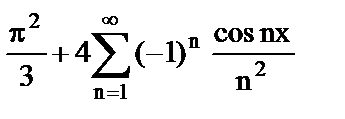
| 2) | Знакочередующийся ряд; |
| в) | 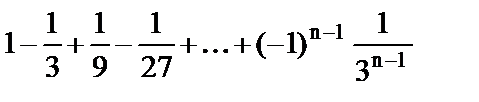
| 3) | Степенной ряд; |
| г) | 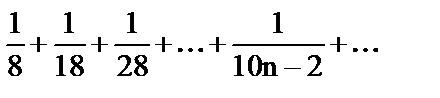
| 4) | Ряд Фурье; |
| д) | 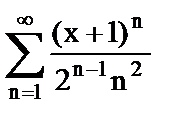
| 5) | Функциональный ряд. |
9. Выбрать правильный ответ.
Ряд 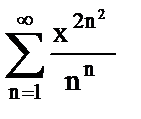 сходится в точке x0,
сходится в точке x0,
а) x0 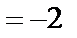 ;
;
б) x0 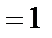 ;
;
в) x0 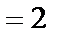 .
.
10. Найти область сходимости ряда
а) 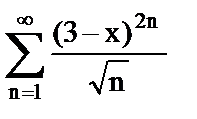 ;
;
б) 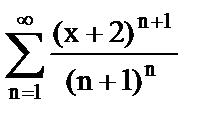 ;
;
в) 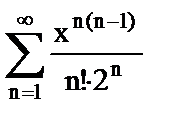 .
.
11. Может ли интервал сходимости ряда 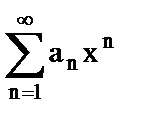 быть таким
быть таким
а) (−2;0);
б) (0;2);
в) (−3;1);
г) (− 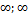 );
);
д)(−3;3).
12. Разложить в ряд Фурье функцию f(x)=x2, заданную на интервале
[− 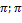 ].
].
13. Разложить в ряд Фурье функцию f(x)=x, заданную на интервале (−3;3).
Ответы
IV. Введение в анализ
1. а); в).
2. а) [ 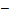 2;2]; б) [0;4]; в) (−∞;0)
2;2]; б) [0;4]; в) (−∞;0) 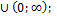 г) (
г) (  ;
; 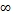 ).
).
3. а) 2; б) 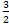 ; г)
; г)  ; в) 0; д)
; в) 0; д)  ; е) 8; ж) 2; з) e8.
; е) 8; ж) 2; з) e8.
4. а); в).
5. а) функция непрерывна; б) х = –2; х = –3 - точки разрыва II рода;
в) x = 4 – точка разрыва II рода.
6. а); г).
7. а1; б1; в1; г4; д2; е1; ж5; з1; и6; к1; л3.
8. а)  ; б) 3; в)
; б) 3; в)  ; г)
; г) 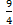 .
.
VII. Комплексные числа
1. а2; б3; в1ю.
2. б) ю.
3. а) 3+ i; б) 4 + 3i; в) i.
4. 215.
X. Кратные интегралы
1. а) 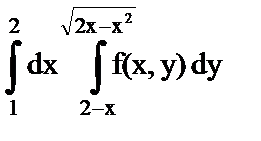 ;
;
б) 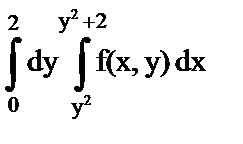

2. а) 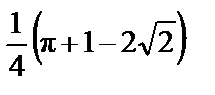 ; б) 26.
; б) 26.
3. б).
4. а) 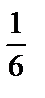 (кв.ед.); б)
(кв.ед.); б) 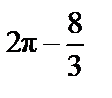 (кв.ед.); в)
(кв.ед.); в) 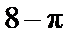 (кв.ед.)
(кв.ед.)
5. а) 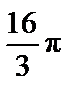 (кв.ед.); б)
(кв.ед.); б) 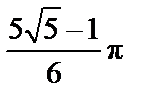 (кв.ед.).
(кв.ед.).
6. а) 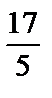 (куб.ед.); б) 90 (куб.ед.).
(куб.ед.); б) 90 (куб.ед.).
7. а4; б3; в1; г6; д2; е5.
8. б).
9. а) 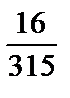 ; б)
; б) 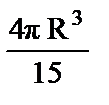 .
.
10. а5; б2; в6; г1; д7; е3; ж4; з8.
11. 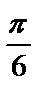 (куб.ед).
(куб.ед).
12. 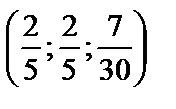 .
.
13. 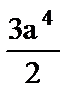 .
.
XII. Ряды
1. а) 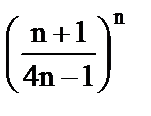 ; б)
; б) 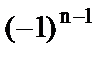 .
.
2. а) 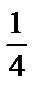 ; б)
; б) 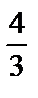 .
.
3. а1; б1; в3; г1, д1;е2.
4. а) расходится; 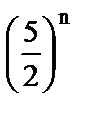 ; б) сходится;
; б) сходится; 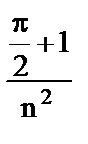 .
.
5. а) расходится; 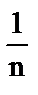 ; б) расходится;
; б) расходится; 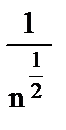 ; в) расходится;
; в) расходится; 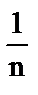 .
.
6. а) расходится, (первый признак сравнения);
б) сходится, (второй признак сравнения);
в) расходится, ( признак Даламбера);
г) сходится, (признак Коши);
д) сходится, (интегральный признак).
7. а) сходится условно;
б) сходится абсолютно;
в) расходится.
8. а5; б4; в2; г1; д3.
9. б).
10. а) 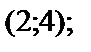 б)
б) 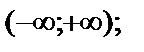 в)
в) 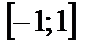 .
.
11. а) нет; б) нет; в) нет; г) да; д) да.
12. 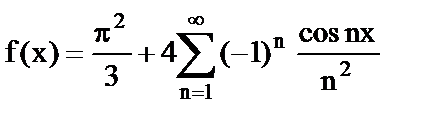 .
.
13. 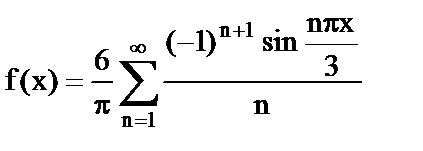 .
.
Список литературы
1. Берман Г. Н. Сборник задач по курсу математического анализа. – CПб.: Профессия, 2006.
2. Выгодский М. Я. Справочник по высшей математике. – М.: Наука, 1977.
3. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч 1: Учеб. пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Мир и образование, 2007.
4. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч 2: Учеб. пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Мир и образование, 2007.
5. Клетеник Д. В. Сборник задач по аналитической геометрии: Уч.пособие для втузов. – 17 изд. –СПб.: Профессия, 2005.
6. Лунгу К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 3-е изд. – М.: Айрис-пресс, 2003.
7. Лунгу К. Н. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу, В. П. Норин, Д. Т. Письменный, Ю. А. Шевченко, Е. Д. Кулагин. – 4-е изд. – М.: Айрис-пресс, 2006.
8. Письменный Д. Т. Конспект лекций по высшей математике: Полный курс. – 2-е изд. – М.: Айрис-пресс, 2004.
9. Сборник задач по математике для втузов. Ч. 1/ под ред. А. В. Ефимова, Б. П. Демидовича. – М.: Наука, 1986.
Составитель Н.А. Смирнова
Задания по математике
в тестовой форме
для организации самостоятельной работы
Учебно-методическое пособие
для студентов
Составитель: Н. А. Смирнова, старший преподаватель
Кафедры ВМ
Дата: 2019-02-02, просмотров: 363.