1. Установить правильное соответствие :
а)  ; ;
| 1) arcsin  + C; + C;
|
б) 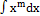 ; ;
| 2) − cos x + C; |
в) 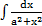 ; ;
| 3) sin x+ C; |
г)  ; ;
| 4) ex + C; |
д) 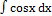 ; ;
| 5) 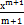 + С; + С;
|
е) 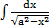 ; ;
| 6) ln 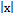 + C; + C;
|
ж) 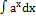 ; ;
| 7) – ln  +C; +C;
|
з) 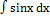 ; ;
| 8) ln 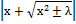 + C; + C;
|
и) 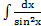 ; ;
| 9)  arctg arctg 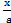 + C; + C;
|
к) 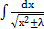 ; ;
| 10) 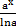 + C; + C;
|
л) 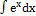 ; ;
| 11) 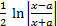 + C; + C;
|
м) 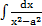 ; ;
| 12) − ctg x+ C; |
н) 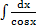 . .
| 13) ln 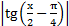 + C. + C.
|
2. Вычислить: 
а) 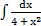 ; ;
| и) 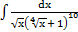 ; ;
|
б) 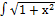 x dx; x dx;
| к) 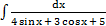 ; ;
|
в) 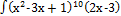 dx; dx;
| л) 
|
г) 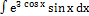 ; ;
| м) 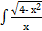 dx; dx;
|
д)  ; ;
| н) 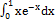 ; ;
|
е) 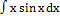 ; ;
| о) 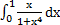 ; ;
|
ж) 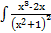 dx; dx;
| п)  ; ;
|
з) 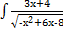 dx; dx;
| р) 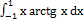 . .
|
3. Почему, не вычисляя интеграла  , можно сказать, что он равен нулю?
, можно сказать, что он равен нулю?
4. Выбрать все правильные ответы.
Определенный интеграл применяется для нахождения:
а) объёма тела вращения;
б) площади плоской фигуры;
в) ускорения тела;
г) длины дуги кривой;
д) площади поверхности вращения;
е) работы переменной силы.
5. Найти площадь фигуры, ограниченной линиями у = sin x, у = cos x, x = 0.
6. Исследовать сходимость интегралов, сходящиеся вычислить:
а) 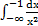 ;
;
б) 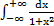 ;
;
в) 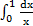 ;
;
г) 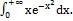
7. Вычислить среднее значение y = 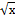 +
+ 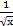 на отрезке [1;4].
на отрезке [1;4].
8. Вычислить длину дуги кривой  от t = 0 до t =
от t = 0 до t =  .
.
9. Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями y2 = x и x2 = y.
10. Оценить интеграл 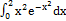 .
.
IX. Дифференциальное исчисление функций нескольких переменных
1. Найти область определения функций:
а) u =  ;
;
б) u = arcsin (x + y);
в) u = y + 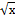 .
.
2. Найти частные производные для функций:
а) u = x2 + 2y2 – 3xy 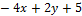 ;
;
б) u = 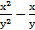 ;
;
в) z = 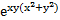 ;
;
г) u =  +
+ 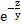 ;
;
д) z = arctg  .
.
3. Найти полный дифференциал функции z = arctg 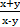 .
.
4. Найти 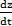 , если z =
, если z = 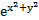 , x = a cos t, y = a sin t.
, x = a cos t, y = a sin t.
5. Составить уравнение касательной плоскости и нормали к поверхности
z = x2 – 2xy+ y2− x + 2y в точке М (1; 1; 1).
6. Вычислить приближенно с помощью дифференциала  .
.
7. Выбрать правильный ответ.
Градиент функции z = x2 + 3y2 в точке А(1;1) равен:
а) {1;6};
б) 9;
в) {1;8};
г) {−1;8}.
8. Найти экстремум функции z = x2+ xy+ y2 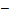 3x
3x 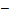 6y.
6y.
9. Найти наибольшее и наименьшее значения функции z = xy + x + y в квадрате , ограниченном прямыми x = 1, x = 2, y = 2, y = 3.
X. Кратные интегралы
1. Изменить порядок интегрирования
а) 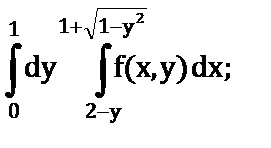
б) 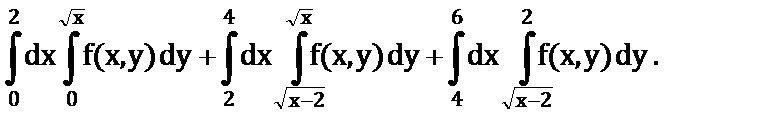
2. Вычислить:
а) 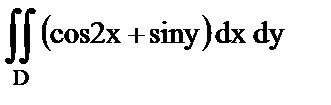 , если область D ограничена линиями
, если область D ограничена линиями 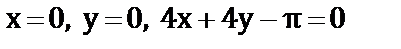 ;
;
б) 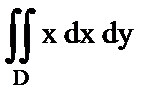 , если D – треугольник с вершинами А(2;3), В(7;2), С(4;5).
, если D – треугольник с вершинами А(2;3), В(7;2), С(4;5).
3. Выбрать правильный ответ.
Якобиан перехода к полярным координатам равен
а) 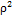 ;
;
б) 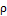 ;
;
в) 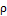 cosφ;
cosφ;
г) 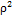 sinφ;
sinφ;
где ρ – полярный радиус, φ – полярный угол.
4. Вычислить площадь фигуры, ограниченной линиями
а) 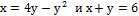 ;
;
б) 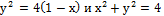 (вне параболы);
(вне параболы);
в) 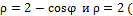 вне кардиоиды).
вне кардиоиды).
5. Вычислить площадь
а) части сферы 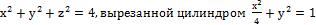 ;
;
б) части поверхности параболоида 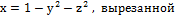
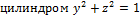 .
.
6. Вычислить объем тел, ограниченных заданными поверхностями
а) 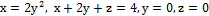 ;
;
б) 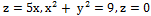 .
.
7. Установить правильное соответствие.
Если γ ‒ поверхностная плотность пластины, D – область плоскости XOY.
| а) Масса плоской пластины; | 1) 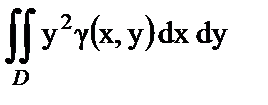 ; ;
|
| б) Статический момент пластины относительно оси OY; | 2) 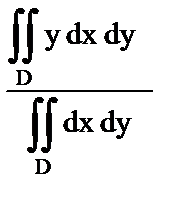 ; ;
|
| в) Момент инерции пластины относительно оси OX; | 3) 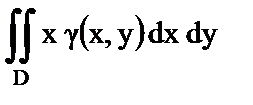  ; ;
|
| г) Момент инерции пластины относительно начала координат; |
4) 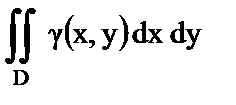 ; ;
|
| д) Ордината центра тяжести однородной пластины; |
5) 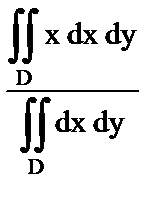 ; ;
|
| е) Абсцисса центра тяжести однородной пластины. |
6) 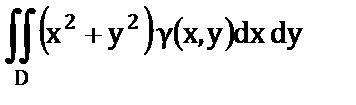 . .
|
8. Выбрать правильный ответ.
Якобиан перехода к сферическим координатам равен
а) 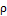 ;
;
б) 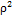 sinθ;
sinθ;
в) 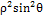 ;
;
г) 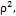
где ρ ‒ полярный радиус, θ ‒ угол между полярным радиусом и осью Оz.
9. Вычислить
а) 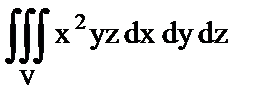 ; если область V ограничена плоскостями
; если область V ограничена плоскостями
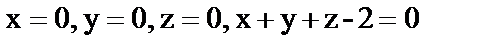 ;
;
б) 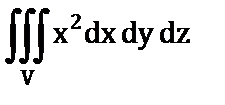 , если V – шар
, если V – шар 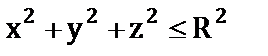 .
.
10. Установить правильное соответствие.
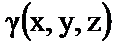 – плотность тела.
– плотность тела.
| а) Объем тела, занимающего область V; | 1) 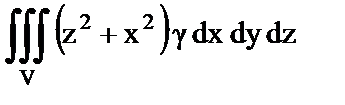 ; ;
|
| б) Масса тела, занимающего область V; | 2) 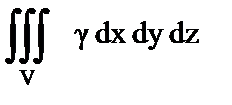 ; ;
|
| в) Апликата центра тяжести тела; | 3) 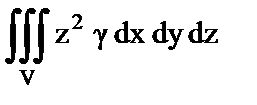 ; ;
|
| г) Момент инерции относительно оси OY; | 4) 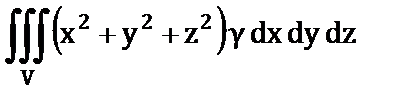 ; ;
|
| д) Абсцисса центра тяжести тела; | 5) 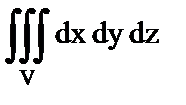 ; ;
|
| е) Момент инерции относительно плоскости XOY; | 6) 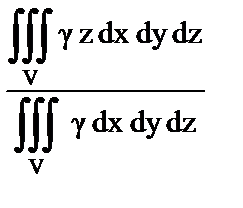 ; ;
|
| ж) Момент инерции относительно начала координат; | 7) 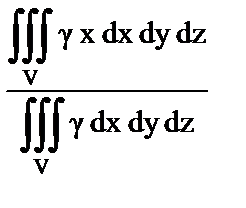 ; ;
|
| з) Статистический момент тела относительно плоскости XOZ. | 8) 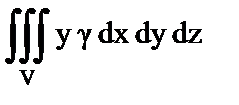 . .
|
11. Вычислить объем тела, ограниченного поверхностями 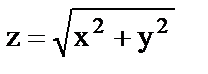 и
и
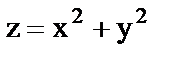 .
.
12. Найти координаты центра тяжести тела, ограниченного поверхностями 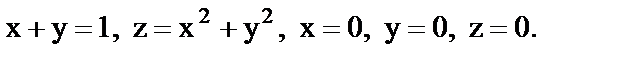
13. Найти массу куба 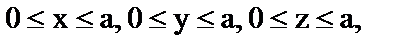 если плотность в точке
если плотность в точке
(x, y, z) есть 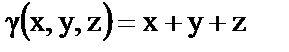 .
.
Дата: 2019-02-02, просмотров: 329.