Водяной пар по своим свойствам существенно отличается от идеального газа, для которого получена формула (33). Поэтому расчёт скорости истечения водяного пара по данной формуле невозможен.

Для вывода формулы конечной скорости вытекающего водяного пара воспользуемся уравнением (26). Перепишем его в следующем виде

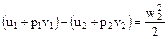                                .                   (44)

Учитывая, что 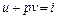, можно записать

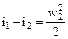                                            .                                     (45)

Таким образом, конечная скорость вытекающего водяного пара равна

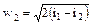                               , м/с.                              (46)

Разность энтальпий 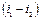 называется располагаемым теплопадением и обозначается h₀. Таким образом,

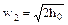                               , м/с.                                  (47)

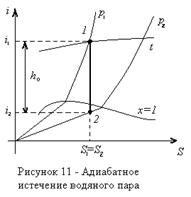
Полезное теплопадение h₀ легко определять с помощью диаграммы i-S водяного пара. Необходимо знать начальное давление и температуру водяного пара и конечное его давление на выходе из сопла. Тогда располагаемое теплопадение будет численно равно отрезку, равному разности энтальпий начала и конца процесса (рисунок 11).

Массовый секундный расход водяного пара определяется из уравнения неразрывности потока (34).

При критическом режиме истечения водяного пара скорость истечения определяется по формуле

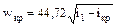                               ,                        (48

где i₁ – энтальпия водяного пара, 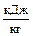, выбирается по таблицам или диаграмме i-S по начальным параметрам;

i_кр – энтальпия водяного пара при критических параметрах, .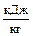

Значение энтальпии i_кр непосредственно определено быть не может, так как обычно неизвестна величина критического давления. Поэтому рекомендуется параметры пара в критическом сечении определять с некоторой погрешностью, используя зависимости, справедливые для идеального газа методом последовательного приближения (по методикам, изложенным в специальной литературе).

Массовый секундный расход определяется из уравнения (34), которое для критического режима истечения водяного пара принимает вид 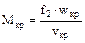                                   ,                                 (49)

где f₂ – площадь «живого» сечения на выходе из сопла;

w_кр – критическая скорость;

v_кр – удельный объём рабочего тела на выходе из сопла при критическом истечении водяного пара.

Форма сопел. Сопло Лаваля

Как уже отмечалось ранее, истечение может быть докритическим, критическим и закритическим. Следует полагать, что каждому виду истечения соответствует своя форма канала, обеспечивающая на выходе из него требуемые характеристики потока. Для анализа возможных форм каналов (сопел) используем уравнение

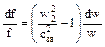,                                                  (50)

где f – площадь выходного сечения сопла;

w₂ – конечная скорость вытекающего рабочего тела;

с_зв – скорость распространения звука в данной среде, которая

    зависит от свойств среды и её параметров.

Поскольку в соплах происходит увеличение скорости, то dw>0 всегда, следовательно, знак df определяется величинами w₂ и c_зв и их отношением.

Здесь возможны три соотношения между указанными скоростями:

1) ;

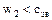2) ;

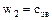3) .

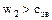Рассмотрим эти соотношения между скоростями w₂ и с_зв.

1 В первом случае будет наблюдаться докритическое истечение, когда давление p₂ больше p_{2 кр.}. Расход не достигает максимального значения. При этом 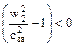,  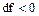и форма канала – суживающееся сопло. (рисунок 12).

2 Во втором случае будет наблюдаться критическое истечение, когда давление p₂ равно давлению p_{2 кр}. Расход рабочего тела становится максимальным. При этом 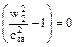и .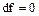

Этот вариант возможен, если к суживающемуся каналу добавить участок с постоянным сечением (рисунок 13).

3 В третьем случае будет наблюдаться закритическое истечение, здесь p₂<p_{2 кр}. При этом 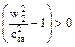,  и форма канала – расширяющееся сопло, на входе в которое газ уже должен иметь критическое давление и звуковую скорость истечения. Таким образом, в этом случае необходимо комбинированное сопло, состоящее из двух частей, а именно из суживающегося канала для достижения скорости газа, равной скорости звука, и расширяющегося канала, в котором скорость газа становится больше скорости звука (рисунок 14).

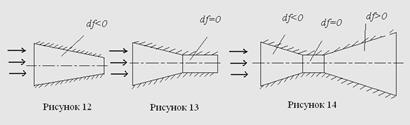
Комбинированное сопло, представленное на рисунке 14, называется соплом Лаваля, разработавшего теорию сопла и впервые применившего его для получения сверхзвуковой скорости пара.

Вопросы для самопроверки

1 Как записывается уравнение первого закона термодинамики для потока?

2 Какое основное отличие диффузоров от сопел?

3 Как вычисляется работа проталкивания?

4 Какая величина называется располагаемой работой, располагаемым теплопадением?

5 По какой формуле можно вычислить конечную скорость вытекающего рабочего тела, ?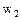

6 По какой формуле вычисляется конечный расход рабочего тела, M₂?

7 Какие виды истечения можно выделить, анализируя график зависимости расхода от отношения давлений?

8 Как вычисляется скорость и расход вытекающего рабочего тела при критическом истечении?

9 Как вычисляется конечная скорость и массовый расход при истечении водяного пара?

10 В чём преимущество сопла Лаваля по сравнению с суживающимся соплом?