Для вывода формулы скорости истечения рабочего тела запишем известное уравнение первого закона термодинамики для потока в дифференциальной форме

                                           dq=du+d 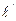+ 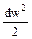,                             (21)

где du - элементарное изменение внутренней энергии, обусловленное изменением температуры потока на выходе из сопла;

      d 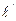- элементарная работа проталкивания, затраченная на проталкивание элементарной массы рабочего тела;

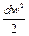    - элементарное изменение кинетической энергии, обусловленное изменением скорости рабочего тела на выходе из сопла.

Интегрируем это уравнение из условия, что истечение адиабатное, следовательно, q=0, dq=0.

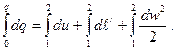                                            (22)

Элементарная работа проталкивания, как известно, равна

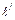                                   d =d( 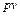).                                               (23)

Учитывая, что dq=0, q=0, после подстановки в уравнение (22) выражения элементарной работы проталкивания из уравнения (23) и интегрирования уравнения (22), имеем

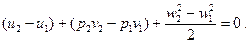                              (24)

Начальная скорость рабочего тела w₁ по сравнению с конечной на выходе из сопла w₂ представляет весьма малую величину и в практических расчетах ею обычно пренебрегают. Отсюда, полагая 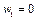, будем иметь

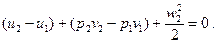                                    (25)

Перепишем полученное выражение в следующем виде:

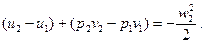                                               (26)

Учитывая, что в адиабатном процессе (при q=0)

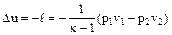                                        (27)

и заменяя в уравнении (26) изменение внутренней энергии на работу адиабатного процесса, получим

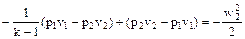                            (28)

Раскрывая скобки и приводя к общему знаменателю левую часть уравнения (28), получим

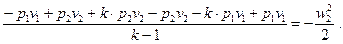       (29)

После преобразования уравнения (29), мы имеем следующее:

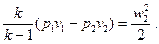                                                          (30)

Левая часть уравнения (30) представляет собой располагаемую работу. Величина этой работы в 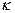раз больше работы расширения газа, как следует из уравнения (27).

Из уравнения (29) выразим :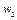

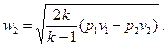                                                     (31)

Вынесем за скобки 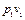 и учитывая, что для адиабатного процесса

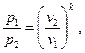                                                                               (32)

окончательно получим следующую формулу:

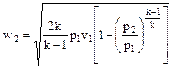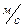                           , .                (33)

Таким образом, полученное уравнение (32) позволяет определять скорость истечения движущегося рабочего тела. Оно справедливо только для идеальных газов.

Для вывода формулы, позволяющей определить массовый расход вытекающего рабочего тела, воспользуемся известным из гидравлики положением, что при стационарном течении газа его массовый расход может быть определен по параметрам в любом сечении сопла. Отсюда, в соответствии с уравнением неразрывности потока, можем записать

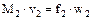                                           ,                                     (34)

где 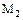- массовый расход вытекающего рабочего тела;

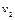        - удельный объём вытекающего рабочего тела на выходе из сопла;

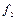 - площадь «живого» сечения на выходе у сопла;

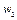 - скорость истечения вытекающего рабочего тела на выходе из сопла.

Тогда массовый расход вытекающего рабочего тела будет равен

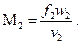                                                                                   (35)

Учитывая, что при адиабатном истечении идеального газа

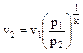                                                                       (36)

и, подставляя в уравнение (35) выражение конечной скорости 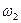 из уравнения (33), будем иметь

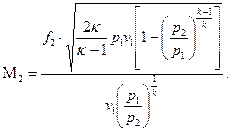                           (37)

   После незначительных преобразований окончательно получим

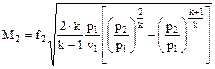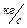                           , .     (38)

Из уравнения (38) следует, что массовый расход идеального газа зависит от площади выходного сечения сопла, начального состояния газа и степени его расширения.