Курс лекций по технической термодинамике и теплотехнике
Часть I
Реальные газы
Уравнение Ван-дер-Ваальса
В реальных газах молекулы имеют конечный объём и связаны между собой силами взаимодействия. При расчете состояний реальных газов нашло широкое применение следующее отношение:
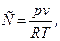 (19)
(19)
где С - коэффициент сжимаемости;
p - абсолютное удельное давление, Па;
v - удельный объём газа, 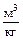 ;
;
R - удельная газовая постоянная, 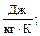
T – абсолютная термодинамическая температура, К.
Для идеальных газов С=1, следовательно, при подстановке этого значения в уравнение (1) будем иметь известное уравнение состояния идеального газа:
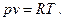
Одной из попыток (и удачной) аналитически описать свойства реальных газов является уравнение, предложенное Ван-дер-Ваальсом. За основу им было выбрано уравнение состояния идеального газа (уравнение 2), в которое введены поправки, учитывающие отличие реального газа от идеального. Первая поправка зависит от объема самих молекул. Представим уравнение (2) в виде
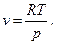 (20)
(20)
Для идеального газа, если p→∞, то v→0. Для реального газа, молекулы которого имеют собственный объём vмол, а также имеют объём зазоров при упаковке vзаз, свободный минимальный объём В, до которого можно сжать газ, будет равен
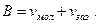 (21)
(21)
С учетом этого, уравнение 3 принимает вид
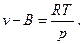
Величина В для каждого газа имеет вполне определённое значение.
Из уравнения (5) выразим удельное абсолютное давление
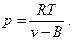 (22)
(22)
Таким образом, при одинаковых условиях (температуре) давление в реальном газе будет больше, т.к. свободный объём будет меньше на величину В, при этом длина свободного пробега молекул будет меньше, следовательно, число соударений молекул больше.
Вторая поправка учитывает влияние сил взаимодействия между молекулами. При наличии этих сил давление в реальном газе будет меньше, так как молекулы соседними частицами будут притягиваться в глубь сосуда. Причем, поправка давления будет прямо пропорциональ-на как числу притягиваемых, так и числу притягивающих молекул. Иначе говоря, она будет прямо пропорциональна квадрату их плотнос-ти. Отсюда можно записать
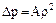 , (23)
, (23)
где ∆p - поправка на давление, учитывающая силы взаимодействия между молекулами;
А - коэффициент пропорциональности, принимающий для каждого
газа определенное числовое значение, не зависящее от параметров состояния;
ρ - плотность газа.
Введя вторую поправку в уравнение (6), имеем
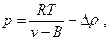
или
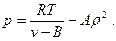 (24)
(24)
Учитывая, что произведение плотности на удельный объем равно единице, уравнение (9) можно записать следующим образом:
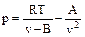 (25)
(25)
Отсюда уравнение Ван-дер-Ваальса принимает вид
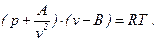 (26)
(26)
Это уравнение было опубликовано Ван-дер-Ваальсом в 1873 г.
Величину 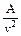 называют внутренним давлением, для жидкостей оно принимает очень большое значение (для воды при T=293 K оно составляет примерно 10800 бар), для газов оно сравнительно невелико и зависит от давления и температуры газа.
называют внутренним давлением, для жидкостей оно принимает очень большое значение (для воды при T=293 K оно составляет примерно 10800 бар), для газов оно сравнительно невелико и зависит от давления и температуры газа.
Уравнение Ван-дер-Ваальса качественно отображает поведение реальных веществ в жидком или газообразном состоянии. Для двухфазных состояний оно неприменимо.
Вопросы для самопроверки
1 Чем отличаются реальные газы от идеальных?
2 Что называется коэффициентом сжимаемости?
3 Как в уравнении Ван-дер-Ваальса учитывается наличие собственного объема молекул?
4 Как в уравнении Ван-дер-Ваальса учитывается наличие сил взаимодействия между молекулами?
5 Какая величина называется внутренним давлением?
6 Для каких состояний рабочего тела применимо это уравнение?
Водяной пар
Основные понятия и определения
Водяной пар широко используется в энергетике, отоплении, для различных технических нужд. Он является рабочим телом в тепловых двигателях (паровых поршневых машинах, паротурбинных установках), а также в различных нагревательных устройствах (теплообменных аппаратах, в нагревательных приборах парового отопления, в калориферах и т. д.), где он используется в качестве теплоносителя.
Процесс парообразования может осуществляться двумя различными по интенсивности и характеру процессами:
1. Испарение – процесс парообразования с поверхности жидкости. Здесь при хаотическом тепловом движении отдельные молекулы, обладающие наибольшей скоростью, преодолевают поверхностное натяжение и вылетают в пространство над поверхностью раздела. Испарение может быть полным, если над жидкостью – неограниченное пространство.
2. Кипение – процесс одновременного и многократного испарения жидкости в область, образованную паровым пузырьком.
Для возникновения кипения температура жидкости должна несколько превышать температуру кипения при данном давлении, т.е. должен быть местный перегрев этой жидкости. При отводе тепла от пара он будет вновь превращаться в жидкость. Этот обратный процесс называется конденсацией. Процесс кипения, так же как и процесс конденсации, протекает при постоянной температуре, если при этом давление рабочего тела не меняется. Жидкость, полученную при конденсации пара, называют конденсатом.
Полученные пары бывают насыщенными и перегретыми.
Насыщенный пар получается в том случае, если в закрытом сосуде наступает момент, когда количество молекул, вылетающих из жидкости, равно числу молекул, возвращающихся обратно в жидкость. Пар в этом состоянии принимает максимальную плотность при данной температуре. То есть, можно сказать, что насыщенный пар – это пар, соприкасающийся с жидкостью и находящийся с ней в термическом равновесии. С изменением температуры равновесие нарушается, вызывая изменение плотности и давления насыщения.
Насыщенные пары, в свою очередь, можно разделить на 2 группы:
1) сухие насыщенные пары;
2) влажные насыщенные пары.
Сухой насыщенный пар получается в результате законченного парообразования, т.е. когда последняя капля жидкости перешла в пар. Это состояние рабочего тела является неустойчивым, т.к. при отводе тепла (или повышении температуры, или повышении давления) часть пара сконденсируется, и рабочее тело будет состоять из смеси пара с жидкостью. Такой пар будет называться влажным насыщенным. Влажный пар может рассматриваться как смесь сухого пара с мельчайшими капельками воды, взвешенными в паре. Его состав определяется степенью сухости x, которая представляет собой долю сухого пара во влажном. Следовательно, (1-х) – влажность пара. (Например, если степень сухости влажного пара х=0,75, то следует, что в рабочем теле 75% сухого пара и 25% - воды).
При незначительном повышении температуры или понижении давления сухой насыщенный пар переходит в состояние перегретого пара, отсюда при одном и том же давлении температура и объем перегретого пара будет больше соответствующих величин сухого пара. Чем больше степень перегрева, тем больше по своим термическим свойствам перегретый пар приближается к идеальному газу. Напротив, при приближении к состоянию насыщения все больше проявляется влияние конечного объема молекул и Ван-дер-Ваальсовых сил.
Пар различного состояния в промышленных условиях получается в паровых котлах (парогенераторах). Процесс парообразования протекает при постоянном давлении, т.е. является изобарным.
Как уже отмечалось, процесс производства пара идет при постоянном давлении. Он включает в себя три последовательных этапа:
- подогрев воды до температуры кипения (она еще называется температурой насыщения и обозначается Ts);
- парообразование, т.е. превращение кипящей жидкости в сухой насыщенный пар;
- перегрев пара до необходимой температуры.
Процесс парообразования в p−ν диаграмме
Диаграмма p-v процесса парообразования строится на основании экспериментальных данных. Проводятся процессы парообразования при различных давлениях (p1, p2, p3 и т.д.), при этом фиксируются состояния воды при температуре насыщения (на диаграмме они обозначаются точками b1, b2, b3 и т.д.). Точками c1, c2, c3 и т.д. фиксируются состояния сухого насыщенного пара для рассматриваемых давлений, а точками d1, d2, d3 и т.д. фиксируются состояния перегретого пара (рисунок 1). Начальное состояние воды на диаграмме обозначается точками a1, a2, a3 и т.д.
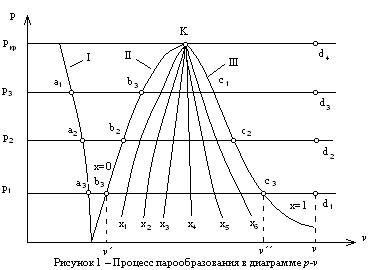
Соединяются точки a1, a2, a3 между собой, точки b1, b2, b3 между собой и точки c1, c2, c3 между собой. При этом на диаграмме получаются три характерные линии.
Линия I – соответствует состояниям воды при начальной температуре и различных давлениях.
Линия II – геометрическое место точек, характеризующих состояние воды при температуре насыщения Ts и различных давлениях. Она называется нижняя пограничная кривая. В любой ее точке у рабочего тела степень сухости равна нулю (х=0).
Линия III – геометрическое место точек, характеризующих состояние сухого насыщенного пара. В любой ее точке у рабочего тела степень сухости равна единице (х=1). Она называется верхняя пограничная кривая.
Линии II и III сходятся в одной точке (К), которая называется критической точкой. Она соответствует некоторому предельному критическому состоянию вещества, при котором исчезают различия между жидкостью и паром. Все параметры, относящиеся к этой точке, называются критическими. Для воды они имеют следующие значения:
pкр=22,06 МПа ;
tкр=374,15°С ;
vкр=0,00326 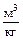 .
.
Между линиями I и II располагается область жидкости, которая нагревается от t=0°C до ts. Между линиями II и III – область влажного насыщенного пара. В этой области можно провести огромное количество линий, соответствующих определенной постоянной степени сухости х. Эти линии получили название линии сухости, они располагаются веерообразно от критической точки К.
Рассматриваемая диаграмма позволяет анализировать процесс кипения при различных давлениях и определять соответствующие параметры рабочего тела.
Вопросы для самопроверки
1 Какой процесс называется испарением?
2 Какой процесс называется кипением?
3 Какой пар называется влажным?
4 Какой пар называется сухим насыщенным?
5 Какой пар называется сухим перегретым?
6 Что характеризует степень сухости влажного пара?
7 Чем характерна критическая точка?
8 Какая линия на диаграмме p-v называется нижней пограничной кривой?
9 Какая линия на диаграмме p-v называется верхней пограничной кривой?
С водяным паром
В связи с тем, что начальное и конечное состояния рабочего тела могут быть заданы различными параметрами, рассмотрим методику расчета основных процессов в общем виде. Расчет заключается в определении основных параметров рабочего тела в начальном и конечном состояниях (p,ν, t, i, s), а также в определении количества тепла, участвующего в процессе, работы и изменения внутренней энергии.
Изобарный процесс (процесс 1-2)
Предположим, что в начале процесса давление рабочего тела Pн=2МН/м2=Pк, степень сухости - x=0.9; в конце рабочего процесса температура рабочего тела возросла до 700 оС.
На диаграмме «s - i» (см. рисунок 3) находим точку пересечения изобары Pн=2МН/м2 и линии сухости, которая и будет соответствовать начальному состоянию рабочего тела (т.1), перемещаясь по изобаре Pн=2МН/м2, находим точку ее пересечения с изотермой t=700оС, которая и будет характеризовать конечное состояние рабочего тела (т.2), т.е. 1-2 изобарный процесс. На диаграмме находим значение всех недостающих параметров для начального и конечного состояний:
| Начальное состояние (т.1) | Конечное состояние (т.2) | ||
| ν 1= | 0.095 м3/кг | ν 2= | 0.22 м3/кг |
| t1= | 214 оС | t2= | 700 оС |
| i1= | 2603 кДж/кг | i2= | 3920 кДж/кг |
| s1= | 5.95 кДж/кг×К | s2= | 7.95 кДж/кг×К |
| P1= | 2 МН/м2 | P2= | 2 МН/м2 |
Используя данные величины, определяем:
1) удельную теплоту, участвующую в процессе, как разность энтальпий начального и конечного состояния рабочего тела
q=i2-i1=3920-2603=1317 кДж/кг;
2) изменение внутренней энергии DU, кДж/кг
DU=[(i2-P2 ν 2)-(i1-P1 ν 1)]=[(3920×103-2.106.0.22)-(2603.103-2.106.0.095)]= =[(3920-440)-(2603-190)].103=1067.103Дж/кг=1067 кДж/кг;
3) удельную работу l, кДж/кг, по формуле
l=p((ν2- ν1)=2.106(0.22-0.095)=0.25.106 Дж/кг=250 кДж/кг
Изохорный процесс (процесс 3-4)
Рассмотрим исследование процесса при следующих исходных данных: удельный объем рабочего тела ν =0.5 м3/кг и остается постоянным, в начале процесса t=800 оС, в конце процесса x=1.
На диаграмме «s-i» (см. рисунок 3) находим точку пересечения изохоры ν =0.5 м3/кг и изотермы t=800 оС, которая и будет характеризовать начальное состояние рабочего тела (т.3).
Перемещаясь по изохоре, найдем точку ее пересечения с линией сухости x=1, которая характеризует конечное состояние рабочего тела в процессе (т.4). По «s-i» - диаграмме находим значение всех параметров рабочего тела для начального и конечного состояний:
Начальное состояние (т.3) Конечное состояние (т.4)
ν3=0.5 м3/кг ν4=0.5 м3/кг
t3=800 оС t4=140 оС
i3=4160 кДж/кг i4=2735 кДж/кг
S3=8.51 кДж/кг.К S4=6.93 кДж/кг.К
P3=0.98 МН/м2 P4=0.37 МН/м2
Используя данные величины, определяем:
удельную теплоту, участвующую в процессе q, кДж/кг; так как в изохорном процессе удельная работа l=0, следовательно, q=∆U, таким образом:
q = ∆U = [(i4-P4 ν4) - (i3-P3 ν3)] = [(2735.103-0.37.106.0.5) -
(4160.103 - 0.98.106.0.5)] = [(2735-185) - (4160-490)].103 =
= -1120.103Дж/кг= -1120 кДж/кг.
Изотермический процесс (процесс 5-6)
Предположим, что начальное состояние рабочего тела характеризуется температурой t=200оС и степенью сухости x=0.85, таким образом, точка пересечения изотермы t=200оС и линии сухости x=0.85 будет соответствовать начальному состоянию рабочего тела в процессе (т.5). Конечное состояние рабочего тела характеризуется объемом ν=5м3/кг, таким образом, точка пересечения изотермы t=200оС и изохоры ν=5м3/кг характеризует конечное состояние рабочего тела в процессе (т.6). По диаграмме «s - i» (см.рисунок 3) находим значение всех параметров рабочего тела для начального и конечного состояний:
| Начальное состояние (т.5) | Конечное состояние (т.6) | ||
| ν5= | 0.12 м3/кг | ν6= | 5 м3/кг |
| t5= | 200 оС | t6= | 200 оС |
| i5= | 2495 кДж/кг | i6= | 2880 кДж/кг |
| s5= | 5.83 кДж/кг×К | s6= | 8.23 кДж/кг×К |
| P5= | 1.5 МН/м2 | P6= | 0.045 МН/м2 |
Используя данные величины, определяем:
1) удельную теплоту, участвующую в процессе q, кДж/кг:
q=T(s6-s5)=(200+273)(8.23-5.85)= 1125.74 кДж/кг;
2) изменение удельной внутренней энергии рабочего тела
DU, кДж/кг:
DU=[(i6-P6V6)-(i5-P5V5)]=[(2880×103-0.045×106×5)-(2495×103-
-1.5×106×0.12)]=[(2880-225)-(2495-180)] ×103=340×103 Дж/кг=340 кДж/кг;
3) удельную работу процесса l, кДж/кг, по формуле
l= q - DU =1125.74-340 = 785.74 кДж/кг.
Адиабатный процесс (процесс 7-8)
Считаем, что начальное состояние рабочего тела характеризуется давлением Р=0.2 МН/м2 и объемом 2 м3/кг, точка пересечения соответствующих изохоры и изобары будет характеризовать начальное состояние рабочего тела в процессе (т.7).
Положим, что в конце процесса температура рабочего тела стала равной t=60 оС. Тогда, для получения точки, характеризующей состояние рабочего тела в конце процесса, из т.7 опускаем вертикальную линию (т.к. s=const) до пересечения с линией температуры t=60 оС (т.8). По диаграмме «s - i» (см. рисунок 3) определяем значение всех параметров рабочего тела в начальном и конечном состоянии:
| Начальное состояние (т.7) | Конечное состояние (т.8) | ||
| ν 7= | 2 м3/кг | ν 8= | 50 м3/кг |
| t7= | 610 оС | t8= | 60 оС |
| i7= | 3722 кДж/кг | i8= | 2618 кДж/кг |
| s7= | 8.8 кДж/кг×К | s8= | 8.8 кДж/кг×К |
| P7= | 0.2 МН/м2 | P8= | 0.003 МН/м2 |
Используя полученные данные, определяем:
1) удельную работу процесса: l, кДж/кг:
т.к. q=0, l=-DU=U7-U8=[(i7-P7V7)-(i8-P8V8)]=[(3722×103-0.2×106×2)-
-(2618×103- 0.003×106×50)]= 854×103Дж/кг=854 кДж/кг;
2) изменение удельной внутренней энергии: DU, кДж/кг:
DU=-l=-854 кДж/кг.
Вопросы для самопроверки
1 Какие основные линии наносятся на диаграмму s-i?
2 Какие три характерные области можно выделить на диаграмме s-i?
3 Как определить удельное количество тепла, участвующее в изобарном процессе, в изотермическом процессе?
4 Как определить удельную работу, совершаемую рабочим телом в изобарном процессе, в адиабатном процессе?
5 Как определяется изменение внутренней энергии и зависит ли оно от вида процесса?
Влажный воздух
Основные понятия и определения
Атмосферный воздух применяется в качестве рабочего тела в различных технологических установках: в системе воздушного отопления, в вентиляционных установках, в сушильных аппаратах. Как правило, он не бывает абсолютно сухим, в нем всегда содержится определенное количество водяного пара. В зависимости от содержания в атмосферном воздухе водяных паров (поэтому он и получил название влажный воздух) различают:
1. Ненасыщенный влажный воздух - влажный воздух, в котором содержание водяных паров меньше максимально возможного при данных условиях.
2. Насыщенный влажный воздух - влажный воздух, в котором содержание водяных паров равно максимально возможному при данных условиях.
3. Перенасыщенный влажный воздух - воздух, в котором влага находится в виде тумана.
К основным характеристикам влажного воздуха относятся:
1) давление влажного воздуха (определяется по закону Дальтона)
Pвл.в.= Pсух.в. + Pвод.п. , (15)
где P, Pвод.п. - парциальное давление сухого воздуха и водяных паров при данных условиях, Н/м2;
2) абсолютная влажность - масса водяных паров (кг), содержащаяся в 1м3 влажного воздуха. Абсолютная влажность представляет собой плотность пара, находящегося во влажном воздухе rвод.п., кг/м3:
= rвод.п (16)
3) относительная влажность - отношение абсолютной влажности к максимально возможной при данных условиях j, %:
j= ·100% , (17)
где rн.п. - плотность насыщенного пара при данных условиях, кг/м3;
4) влагосодержание - количество водяного пара, приходящегося на 1 кг сухого воздуха, которое находится во влажном воздухе d , г.вод.п./кг.сух.в. :
d=Mвод.п./Mсух.в.×1000=622× , (18)
где Mвод.п.,Mсух.в. - соответственно массы водяных паров и сухого воздуха, кг;
Pвод.п.- парциальное давление водяных паров, Н/м2;
Pбар. - барометрическое давление, Н/м2.
Исходя из этого, воздух рассматривается как смесь 1 кг сухого воздуха и d/1000 кг водяного пара. И в этом случае количество влажного воздуха будет составлять (1+ d/1000) кг
5) энтальпия влажного воздуха hвл.в., кДж/кг сух.в.
hвл.в.= hсух.в. + hвод.п.= Срсух.в.×t+(2490+1,97×t)×d/1000, (19)
где hсух.в., hвод.п. - соответственно энтальпия сухого воздуха и водяных паров при данных условиях, кДж/кг;
d – влагосодержание, г.вод.п./кг.сух.в.;
Срсух.в. - теплоемкость сухого воздуха в изобарном процессе, кДж/кг×К;
t - температура влажного воздуха, оС
6) объем влажного воздуха рассматривается как объем сухой части воздуха во влажном воздухе
Vвл.в.=Rсух.в.×T/Pсух.в. , (20)
где Rсух.в. - удельная газовая постоянная сухого воздуха, Дж/кг×К;
Т - абсолютная температура воздуха, К;
Pсух.в. - парциальное давление сухого воздуха, Н/м2.
Диаграммы « h - d »
1 Нагревание воздуха - на диаграмме «h - d» изображается прямой линией d=const , направленной вверх от точки, характеризующей начальные параметры воздуха, до конечной температуры.
2 Охлаждение воздуха - изображается прямой линией d=const , направленной вниз от точки, характеризующей начальные параметры воздуха, до конечной температуры.
3 Адиабатное испарение воды - на диаграмме «h - d» пойдет по линии i=const .
4 Определение температуры точки росы.
Точкой росы называется та наиболее низкая температура, до которой можно охладить влажный воздух при постоянном его влагосодержании. При дальнейшем охлаждении воздуха содержащийся в нем водяной пар будет выпадать в виде конденсата.
Для определения температуры точки росы из точки, характеризующей начальное состояние воздуха, опускаем вниз линию d=const до пересечения с линией j=100%. Изотерма, проходящая через эту точку, и соответствует температуре точки росы.
Истечение газов и паров
Истечение – процесс прохождения газа или пара по каналам особой формы.
Если при перемещении по каналу происходит расширение рабочего тела с уменьшением давления и увеличением скорости, то такой канал называют соплом.
Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором. Возьмём канал переменного сечения, по которому перемещается идеальный газ (рисунок 9).
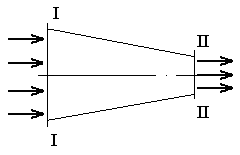
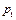
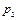
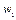
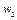
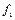
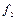

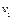
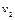
Рисунок 9
Выделим два сечения I-I и II-II. В сечении I-I удельный объём рабочего тела v1, давление газа p1, скорость движения w1, площадь «живого» сечения f 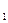 . Аналогично в сечении II-II. Удельный объём v2, давление p2, скорость движения w2, площадь «живого» сечения f
. Аналогично в сечении II-II. Удельный объём v2, давление p2, скорость движения w2, площадь «живого» сечения f 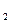 . Пусть давление p1> p2, следовательно, рассматривается истечение рабочего тела через сопло. Исследования показали, что в каналах даже при небольшой разности давлений газа и внешней среды получается достаточно большая скорость течения рабочего тела.
. Пусть давление p1> p2, следовательно, рассматривается истечение рабочего тела через сопло. Исследования показали, что в каналах даже при небольшой разности давлений газа и внешней среды получается достаточно большая скорость течения рабочего тела.
Поскольку длина канала обычно небольшая, то теплообмен между стенками канала и рабочим телом при малом времени их прохождения настолько незначителен, что им можно пренебречь и процесс истечения можно считать адиабатным. При решении задач на истечение газов и паров, как правило, требуется определить скорость истечения, секундный расход рабочего тела, форму сопла, по которому движется рабочее тело.
Форма сопел. Сопло Лаваля
Как уже отмечалось ранее, истечение может быть докритическим, критическим и закритическим. Следует полагать, что каждому виду истечения соответствует своя форма канала, обеспечивающая на выходе из него требуемые характеристики потока. Для анализа возможных форм каналов (сопел) используем уравнение
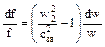 , (50)
, (50)
где f – площадь выходного сечения сопла;
w2 – конечная скорость вытекающего рабочего тела;
сзв – скорость распространения звука в данной среде, которая
зависит от свойств среды и её параметров.
Поскольку в соплах происходит увеличение скорости, то dw>0 всегда, следовательно, знак df определяется величинами w2 и cзв и их отношением.
Здесь возможны три соотношения между указанными скоростями:
1) 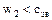 ;
;
2) 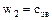 ;
;
3) 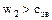 .
.
Рассмотрим эти соотношения между скоростями w2 и сзв.
1 В первом случае будет наблюдаться докритическое истечение, когда давление p2 больше p2 кр.. Расход не достигает максимального значения. При этом 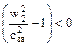 ,
, 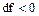 и форма канала – суживающееся сопло. (рисунок 12).
и форма канала – суживающееся сопло. (рисунок 12).
2 Во втором случае будет наблюдаться критическое истечение, когда давление p2 равно давлению p2 кр. Расход рабочего тела становится максимальным. При этом 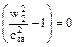 и
и 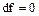 .
.
Этот вариант возможен, если к суживающемуся каналу добавить участок с постоянным сечением (рисунок 13).
3 В третьем случае будет наблюдаться закритическое истечение, здесь p2<p2 кр. При этом 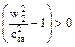 ,
, 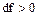 и форма канала – расширяющееся сопло, на входе в которое газ уже должен иметь критическое давление и звуковую скорость истечения. Таким образом, в этом случае необходимо комбинированное сопло, состоящее из двух частей, а именно из суживающегося канала для достижения скорости газа, равной скорости звука, и расширяющегося канала, в котором скорость газа становится больше скорости звука (рисунок 14).
и форма канала – расширяющееся сопло, на входе в которое газ уже должен иметь критическое давление и звуковую скорость истечения. Таким образом, в этом случае необходимо комбинированное сопло, состоящее из двух частей, а именно из суживающегося канала для достижения скорости газа, равной скорости звука, и расширяющегося канала, в котором скорость газа становится больше скорости звука (рисунок 14).
Комбинированное сопло, представленное на рисунке 14, называется соплом Лаваля, разработавшего теорию сопла и впервые применившего его для получения сверхзвуковой скорости пара.
Вопросы для самопроверки
1 Как записывается уравнение первого закона термодинамики для потока?
2 Какое основное отличие диффузоров от сопел?
3 Как вычисляется работа проталкивания?
4 Какая величина называется располагаемой работой, располагаемым теплопадением?
5 По какой формуле можно вычислить конечную скорость вытекающего рабочего тела, 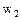 ?
?
6 По какой формуле вычисляется конечный расход рабочего тела, M2?
7 Какие виды истечения можно выделить, анализируя график зависимости расхода от отношения давлений?
8 Как вычисляется скорость и расход вытекающего рабочего тела при критическом истечении?
9 Как вычисляется конечная скорость и массовый расход при истечении водяного пара?
10 В чём преимущество сопла Лаваля по сравнению с суживающимся соплом?
Часть II
Вопросы для самопроверки
1 Какие процессы называются круговыми или циклами?
2 На какие два вида делятся круговые процессы в зависимости от знака  полезной работы цикла?
полезной работы цикла?
3 Как записывается выражение первого закона термодинамики для круговых процессов?
4 Каким коэффициентом оценивается эффективность прямых циклов, как он вычисляется?
5 Каким коэффициентом оценивается эффективность обратных циклов, как он вычисляется?
Вопросы для самопроверки
1 Какие принимаются допущения при разработке идеальных циклов ДВС?
2 Как изображается в P-V и T-S диаграммах идеальный цикл ДВС с изохорным подводом тепла?
3 Что понимается под степенью сжатия 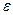 , как величина степени сжатия влияет на термический к.п.д. цикла с изохорным подводом тепла?
, как величина степени сжатия влияет на термический к.п.д. цикла с изохорным подводом тепла?
4 Как изображается в P-V и T-S диаграммах цикл ДВС с изобарным подводом тепла?
5 По какой формуле вычисляется термический к.п.д. цикла с изобарным подводом тепла?
6 Как изображается в P-V и T-S диаграммах цикл ДВС со смешанным подводом тепла?
7 Как сказывается на величине термического к.п.д. цикла со смешанным подводом тепла повышение степени сжатия 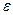 , степени повышения давления
, степени повышения давления 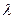 и степени предварительного расширения
и степени предварительного расширения 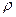 ?
?
8 При одинаковой степени сжатия и одинаковом рабочем теле какой из трёх циклов ДВС будет иметь больший к.п.д.?
9 При разных степенях сжатия цикл с изохорным подводом тепла или со смешанным подводом тепла будет иметь больший термический к.п.д.?
10 Какие основные недостатки присущи ДВС?
Установки (ГТУ)
Газотурбинные установки нашли широкое применение в авиации, на речных и морских судах, в военной технике, на электростанциях, в газовой и нефтяной промышленности, на нефтеперерабатывающих заводах, для привода насосов и компрессоров на магистральных газо и нефтепроводах, на металлургических заводах, предприятиях химической промышленности.
Основными преимуществами ГТУ по сравнению с поршневыми ДВС являются:
1 - отсутствие деталей с возвратно-поступательным движением;
2 - относительно малый вес и габариты;
3 - возможность выполнения газовых турбин с большими числами оборотов и большими единичными мощностями;
4 - более высокий к.п.д.
Принципиальная схема ГТУ представлена на рисунке (5)
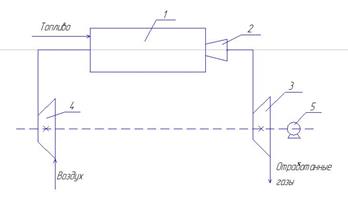
1 – камера сгорания; 2 – комбинированное сопло;
3 – газовая турбина; 4 – компрессор;
5 – электрогенератор или редуктор.
Рисунок 5 – Принципиальная схема ГТУ
Воздух, поступающий в компрессор, сжимается до определённого давления и подаётся в камеру сгорания. Одновременно с воздухом в камеру сгорания подаётся и топливо. Образовавшиеся продукты сгорания топлива проходят через комбинированное сопло, где резко возрастает их скорость, а следовательно и кинетическая энергия. С большой скоростью продукты сгорания попадают на лопатки турбины, вращая колесо турбины, которое жёстко закреплено на валу. На этом же валу расположен и компрессор, т.е. часть мощности газовой турбины расходуется на привод. В зависимости от назначения ГТУ на валу может быть установлен электрогенератор, если установка применяется для производства электрической энергии, или редуктор, если установка используется в качестве газотурбинного двигателя.
В ГТУ наблюдаются следующие преобразования энергии:
1 - в камере сгорания химическая энергия топлива преобразуется во внутреннюю энергию продуктов сгорания топлива;
2 - в комбинированном сопле внутренняя энергия преобразуется в кинетическую энергию потока продуктов сгорания;
3 - на турбине кинетическая энергия потока преобразуется в механическую энергию вращения вала турбины;
4 - в электрогенераторе механическая энергия вращения вала турбины преобразуется в электрическую.
Для простейших ГТУ разработаны два идеальных цикла:
1 - с изохорным подводом тепла;
2 - с изобарным подводом тепла.
При разработке циклов ГТУ были приняты допущения:
1 - цикл замкнут, он осуществляется с постоянным количеством идеального газа, имеющего неизменный химический состав и постоянную теплоёмкость;
2 - все процессы в цикле являются обратимыми, так как они протекают без тепловых и гидравлических потерь;
3 - сжатие в компрессоре и расширение в сопловом аппарате происходят адиабатно, то есть при постоянном значении энтропии.
Вопросы для самопроверки
1 Чем вызвано создание газовых турбин?
2 Каковы преимущества газовых турбин перед ДВС?
3 Какие основные элементы входят в принципиальную схему ГТУ?
4 Как изображается в P-V диаграмме цикл ГТУ с изохорным подводом тепла?
5 По какой формуле вычисляется 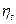 цикла ГТУ с изохорным подводом тепла?
цикла ГТУ с изохорным подводом тепла?
6 Почему цикл ГТУ с изохорным подводом тепла не нашёл широкого применения?
7 Из каких процессов составлен цикл ГТУ с изобарным подводом тепла?
8 Вывести выражение для термического к.п.д. цикла ГТУ с подводом тепла при 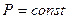 .
.
9 Какие важнейшие задачи необходимо решить для создания крупных стационарных ГТУ?
Рисунок 9 - Цикл Ренкина в P-V и T-S координатах
процесс 1-2 - адиабатное расширение водяного перегретого пара от давления P1 до давления в конденсаторе P2;
процесс 2-21 - процесс конденсирования водяного пара в конденсаторе при давлении P2;
процесс 21-3 - сжатие воды в насосе, здесь повышение температуры воды очень мало и им пренебрегают;
процесс 3-4 - изображает изменение объёма воды при нагреве её до температуры кипения;
процесс 4-5 - процесс парообразования в паровом котле, при этом образуется влажный насыщенный пар;
процесс 5-6 - процесс подсушивания пара в пароперегревателе
до х=1;
процесс 6-1 - процесс перегрева пара в пароперегревателе при давлении P1.
Термический КПД цикла Ренкина определяется по уравнению
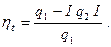 (55)
(55)
Теплота q1 в цикле подводится при p=const в процессах 3-4, 4-6, 6-1 и для 1кг пара эта теплота равна:
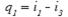 (56)
(56)
Это количество теплоты в диаграмме T-S изображается площадью 8-21-3-4-6-1-7-8. Теплота q2 отводится в конденсаторе по изобаре 2-21 (давление P2), следовательно:
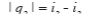 (57)
(57)
Это количество теплоты в диаграмме T-S изображается
площадью 2-21-8-7-2. Тогда термический КПД цикла определяется по уравнению:
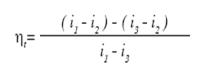 (58)
(58)
В практических расчетах вводятся допущения: не учитывают повышения температуры воды при адиабатном сжатии воды в насосе; полагают, что изобары жидкости сливаются с нижней пограничной кривой; пренебрегают работой насоса. Отсюда КПД цикла Ренкина с учетом принятых допущений вычисляется по уравнению:
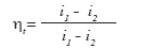 (59)
(59)
Значения энтальпий выбираются по таблицам водяного пара или по диаграмме i-S.
Компрессоры
Компрессор - это машина, предназначенная для сжатия и перемещения различных газов. Компрессоры используются в химической, машиностроительной, металлургической, горнорудной и др., на железных дорогах, в авиации, в ГТУ и т.д.
Все компрессоры, в зависимости от конструктивного оформления и принципа работы, подразделяются на две группы:
- поршневые
- турбинные (центробежные)
Однако, термодинамика процессов сжатия в них одинакова. Процессы в них описываются одними и теми же уравнениями. Поэтому рассмотрим работу наиболее простого одноступенчатого компрессора (поршневого).
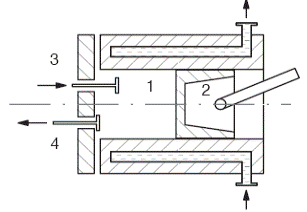
Рисунок 11 - Поршневой компрессор
Компрессор состоит из цилиндра 1 с пустотелыми стенками, в которых циркулирует охлаждающая вода, и поршня 2, связанного кривошипно-шатунным механизмом с электродвигателем или другим источником механической работы. В крышке цилиндра в специальных коробках помещаются два клапана: всасывающий 3 и нагнетательный 4, которые открываются автоматически под действием изменения давления в цилиндре.
Рабочий процесс компрессора совершается за один оборот вала (или два хода поршня). При ходе поршня вправо открывается всасывающий клапан и в цилиндр поступает рабочее тело - газ. При обратном движении поршня всасывающий клапан закрывается, происходит сжатие газа до требуемого давления и нагнетание его в резервуар.
Рассмотрим работу теоретического одноступенчатого компрессора.
Примем допущения:
1 Геометрический объём цилиндра равен рабочему объёму, т.е. отсутствует вредное пространство.
2 Отсутствуют потери работы на трение поршня о стенки цилиндра.
3 Отсутствует дросселирование в клапанах.
4 Всасывание газа и его нагнетание происходят при постоянном давлении.
Покажем цикл компрессора в P-V диаграмме.
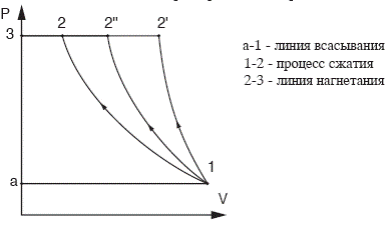
Рисунок 12 - Циклы компрессора в P-V диаграмме
Линии а-1 и 2-3 не являются процессами, так как состояние рабочего тела в них не изменяется, а изменяется его количество.
Найдём затраченную работу L на получение 1кг сжатого газа (без учета трения).
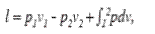 (60)
(60)
где p1v1 --работа, производимая внешней средой при
заполнении цилиндра газом;
p2v2 - работа, затраченная на выталкивание газа.
Процесс сжатия в компрессоре может осуществляться по изотерме (1-2), по адиабате (1-21), по политропе (1-2”). Затраченная работа в каждом из этих случаев сжатия газа будет различной.
При изотермическом сжатии (1-2)
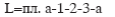
и имеет наименьшую величину. Здесь вся энергия, подводимая в форме работы, отводится от газа в форме теплоты.
Сжатие по адиабате (1-21) даёт наибольшую площадь:
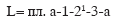
и, следовательно, наибольшую затрату работы.
При политропном сжатии величина работы принимает промежуточное значение:
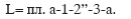
Таким образом, чтобы уменьшить работу сжатия, необходимо процесс сжатия приблизить к изотермическому. Поэтому в реальном компрессоре и применяют охлаждение водой, которая протекает через рубашку компрессора, образуемую полыми стенками цилиндра. Охлаждение дает возможность сжимать газ до более высоких давлений в политропном процессе при n = 1,18...1,2. У компрессоров малой производительности при небольших давлениях сжатого газа стенки цилиндра делают ребристыми. Ребра обдуваются воздухом и, тем самым, цилиндр охлаждается.
Многоступенчатый компрессор
Многоступенчатые компрессоры применяются для получения газа высокого давления. В них сжатие газа осуществляется в нескольких последовательно соединенных цилиндрах, с промежуточным охлаждением газа после его каждого сжатия. Промежуточное охлаждение газа улучшает условия смазки поршня в цилиндре и уменьшает расход энергии на привод компрессора. При этом рабочий процесс приближается к изотермическому (наиболее выгодному).
Покажем идеальную индикаторную диаграмму 3х ступенчатого компрессора.
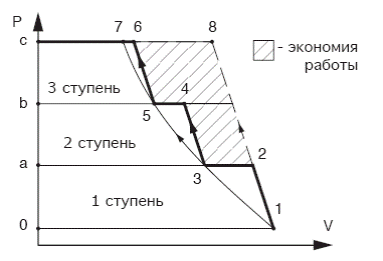
0-1 линия всасывания в первую ступень;
1-2 политропный процесс сжатия в первой ступени;
2-а линия нагнетания из первой ступени в первый охладитель;
а-3 линия всасывания во вторую ступень;
3-4 политропный процесс сжатия во второй ступени;
4-в линия нагнетания из второй ступени во второй охладитель;
в-5 линия всасывания в третью ступень;
5-6 линия сжатия в третьей ступени;
6-с линия нагнетания в резервуар.
Рисунок 13 - Идеальная индикаторная диаграмма
Охлаждение газа во всех охладителях производится до температуры Т1, поэтому: Т3 = Т5 = Т1
Отношение давлений во всех ступенях обычно берется одинаковым:
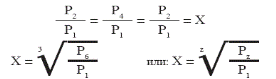 (61)
(61)
где Z - число ступеней.
Вся работа на привод 3х ступенчатого компрессора при
политропном сжатии газа определяется (для 3х ступенчатого):
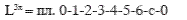
Если бы сжатие проводилось в одноступенчатом компрессоре, то работа была бы равна:
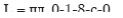
т.е., как следует из диаграммы P-V
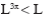
Покажем в T-S диаграмме процессы сжатия в 3х ступенчатом компрессоре.
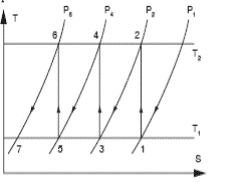
Рисунок 14 – Адиабатное сжатие в ступени
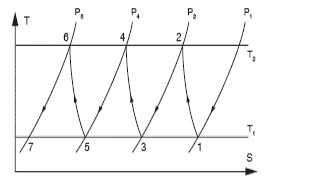
Рисунок 15 - Политропное сжатие газа в ступени
При политропном и адиабатном сжатии газа в каждой ступени в охладителях отводится одно и то же количество теплоты.
Вопросы для самопроверки
1 Каково назначение компрессора?
2 В чем отличие одноступенчатого компрессора от многоступенчатого?
3 Какие процессы возможны при сжатии газа в компрессоре?
4 Какой процесс сжатия является наивыгоднейшим и почему?
5 При каком процессе в компрессоре затрачивается наибольшая работа?
6 Какими уравнениями определяется работа на привод компрессора при изотермическом, адиабатном и политропном сжатии рабочего тела?
7 Почему нельзя получить газ высокого давления в одноступенчатом компрессоре?
8 Как изображается в P-V диаграмме идеальная индикаторная диаграмма 3 х ступенчатого компрессора?
9 Как изображается в T – S диаграмме адиабатное и политропное сжатие газа в ступени?
Тепловой насос
Это - установка, при помощи которой теплота низкого потенциала, забираемая из окружающей среды с помощью затраченной извне работы, при более высокой температуре отдаётся внешнему потребителю (т.е. работает по циклу холодильных установок).
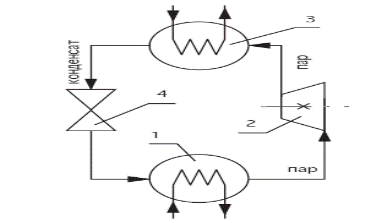
1 – испаритель; 2 – компрессор; 3 – конденсатор; 4 - дроссельный вентиль
Рисунок 16 - Схема теплового насоса
Работа теплового насоса состоит в следующем: за счет теплоты источника с низкой температурой в испарителе происходит процесс парообразования рабочего тела с низкой температурой кипения (фреон, аммиак). Полученный пар направляется в компрессор, в котором его температура повышается. Затем пар поступает в конденсатор, где отдаёт своё тепло жидкости, например, циркулирующей в системе отопления.
Образовавшийся конденсат рабочего тела направляется в дроссельный вентиль, где происходит снижение его давления и, соответственно, температуры. И рабочее тело вновь поступает в испаритель.
Такая схема может успешно работать, например, на Дальнем Востоке, где имеется огромное количество горячих природных источников.
Целесообразно её применять в стационарных ДВС. Здесь в качестве источника теплоты с низкой температурой можно использовать воду, которая охлаждает цилиндры двигателя.
Можно использовать и тепло воды, которая охлаждает цилиндры компрессорной установки.
Характеристикой совершенства работы теплового насоса будет:
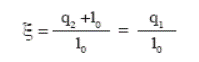 (62)
(62)
где q1 - теплота, отданная внешнему потребителю;
l - затраченная работа в компрессоре;
q2 - теплота, полученная фреоном в испарителе.
Покажем на примере эффективность работы теплового насоса.
Если установка работает по обратному циклу Карно, то при Т2 = 280 К и Т1 = 350 К, отсюда
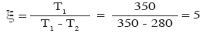
т.е. передаётся теплоты в 5 раз больше, чем затрачивается работы.
Вопросы для самопроверки
1 Каково назначение теплового насоса?
2 Каков принцип действия теплового насоса?
3 В каких случаях целесообразно применять тепловой насос для отопления зданий?
4 Какие преимущества имеет тепловой насос по сравнению с непосредственным использованием электроэнергии для отопления?
5 Что такое отопительный коэффициент, как он вычисляется?
Эжектирование
Эжектирование - процесс приведения в движение газа под действием разрежения. Это разрежение создаётся другим газом, движущимся с большой скоростью. Газ, который создаёт разрежение, называется эжектирующим (активным), а газ, который приводится в движение - эжектируемым (пассивным).
В процессе эжектирования в результате турбулентного смешения газов происходит выравнивание скоростей и параметров этих газов.
Различают:
1 - эжекторы (струйные вентиляторы).
2 - инжекторы (струйные насосы и компрессоры).
Рассмотрим принципиальную конструкцию эжектора:
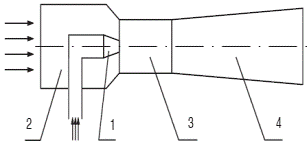
1 - сопло высоконапорного эжектирующего газа (активного).
2 - сопло низконапорного эжектируемого газа (пассивного).
3 - камера смешения, которая бывает цилиндрической или прямоугольной.
4 - диффузор.
Рисунок 17 - Конструкция эжектора
- В эжекторе количество эжектирующего газа меньше, как правило, эжектируемого. Статическое давление их смеси на выходе равно давлению окружающей среды. Эжекторы находят применение для вентиляции помещений, для удаления из различных установок отработавших газов и т. д.
- В инжекторах количество эжектирующего газа обычно больше, чем эжектируемого. Он предназначен для повышения давления газов и паров, для нагнетания жидкости в резервуары и различные устройства. По устройству и принципу действия эжекторы и инжекторы практически одинаковы.
Вопросы для самопроверки
1 Какой процесс называется эжектированием?
2 Какой газ называется эжектирующим?
3 Какой газ называется эжектируемым?
4 Какова принципиальная конструкция эжектора?
5 В чем принципиальное отличие эжектора от инжектора?
СПИСОК ЛИТЕРАТУРЫ
1 Теплотехника. Учеб. для вузов /В.Н.Луканин, М.Г. Шатров, Г.М.Камфер и др.; под ред. В.Н.Луканина - 3-е изд., испр. - М.: Высшая школа, 2002. - 671 с.
2 Теплотехника: учебник для втузов /Под общей ред. А.М.Архарова, В.Н.Афанасьева - 2-е изд., перераб. и доп. - М.: Изд-во МГТУ им.Н.Э.Баумана, 2004. - 712 с.
3 Техническая термодинамика и теплотехника: учебн. пособие для вузов /Под ред. А.А.Захаровой - М.: Издательский центр«Академия», 2006. - 272 с.
4 Юдаев Б.Н. Техническая термодинамика. Теплопередача - М.: Высшая школа, 1986. - 480 с.
5 Жуковский В.С. Термодинамика - М.: Энергоатомиздат, 1983. - 304 с.
6. Техническая термодинамика /Под ред. В.И.Крутова: учебник для втузов. - М.: Машиностроние, 1986. - 472 с.
7 Теплотехника. Учебник для вузов /Под ред. А.П.Баскакова, 2-е изд., перераб. - М.: Энергоатомиздат, 1991. - 224 с.
8 Нащокин В.В. Техническая термодинамика и теплопередача: учебн. пособие для вузов. - М.: Высшая школа, 1975. - 496 с.
СОДЕРЖАНИЕ
с.
Уравнение Ван-дер-Ваальса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Водяной пар. Основные понятия и определения . . . . . . . . . . . . . . . . 3
Процесс парообразования в p−ν диаграмме . . . . . . . . . . . . . . . . . . . . 5
T-s диаграмма водяного пара . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Диаграмма s-i водяного пара . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Графоаналитический метод расчета основных процессов
с водяным паром . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Влажный воздух. Основные понятия и определения . . . . . . . . . . . . 14
Диаграмма «h - d» влажного воздуха . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Расчет процессов с влажным воздухом с помощью
диаграммы «h - d» . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Истечение газов и паров . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Скорость истечения и массовый расход рабочего тела . . . . . . . . . . 23
Анализ уравнения массового расхода идеального газа.
Критическое давление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Критическая скорость и максимальный секундный расход
идеального газа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Адиабатное истечение водяного пара . . . . . . . . . . . . . . . . . . . . . . . . . 29
Форма сопел. Сопло Лаваля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Дросселирование газов и паров . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Дросселирование, или мятие, водяного пара . . . . . . . . . . . . . . . . . . . 34
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Круговые процессы (циклы). Общие сведения . . . . . . . . . . . . . . . . . . 37
Термический к.п.д. и холодильный коэффициент циклов . . . . . . . . . 39
Двигатели внутреннего сгорания. Общие сведения . . . . . . . . . . . . . . 40
Идеальные циклы двигателей внутреннего сгорания (ДВС) . . . . . . . 42
Цикл ДВС с изохорным подводом тепла . . . . . . . . . . . . . . . . . . . . . . . 42
Цикл ДВС с изобарным подводом тепла . . . . . . . . . . . . . . . . . . . . . . . 47
Цикл ДВС со смешанным подводом тепла . . . . . . . . . . . . . . . . . . . . . 50
Газотурбинные установки (ГТУ). Общие сведения.
Принципиальная схема газотурбинной установки (ГТУ) . . . . . . . . . . 54
Идеальный цикл ГТУ с изохорным подводом тепла . . . . . . . . . . . . . 56
Цикл ГТУ с подводом теплоты в процессе P = const . . . . . . . . . . . . . . 59
Циклы паротурбинных установок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
Влияние основных параметров на величину к.п.д. цикла Ренкина . . 66
Магнитогидродинамический генератор (МГД-генератор) . . . . . . . . 67
Компрессоры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Многоступенчатый компрессор . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Тепловой насос . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
Эжектирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
Содержание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Курс лекций по технической термодинамике и теплотехнике
Часть I
Реальные газы
Уравнение Ван-дер-Ваальса
В реальных газах молекулы имеют конечный объём и связаны между собой силами взаимодействия. При расчете состояний реальных газов нашло широкое применение следующее отношение:
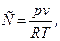 (19)
(19)
где С - коэффициент сжимаемости;
p - абсолютное удельное давление, Па;
v - удельный объём газа, 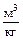 ;
;
R - удельная газовая постоянная, 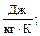
T – абсолютная термодинамическая температура, К.
Для идеальных газов С=1, следовательно, при подстановке этого значения в уравнение (1) будем иметь известное уравнение состояния идеального газа:
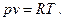
Одной из попыток (и удачной) аналитически описать свойства реальных газов является уравнение, предложенное Ван-дер-Ваальсом. За основу им было выбрано уравнение состояния идеального газа (уравнение 2), в которое введены поправки, учитывающие отличие реального газа от идеального. Первая поправка зависит от объема самих молекул. Представим уравнение (2) в виде
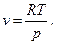 (20)
(20)
Для идеального газа, если p→∞, то v→0. Для реального газа, молекулы которого имеют собственный объём vмол, а также имеют объём зазоров при упаковке vзаз, свободный минимальный объём В, до которого можно сжать газ, будет равен
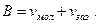 (21)
(21)
С учетом этого, уравнение 3 принимает вид
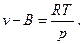
Величина В для каждого газа имеет вполне определённое значение.
Из уравнения (5) выразим удельное абсолютное давление
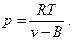 (22)
(22)
Таким образом, при одинаковых условиях (температуре) давление в реальном газе будет больше, т.к. свободный объём будет меньше на величину В, при этом длина свободного пробега молекул будет меньше, следовательно, число соударений молекул больше.
Вторая поправка учитывает влияние сил взаимодействия между молекулами. При наличии этих сил давление в реальном газе будет меньше, так как молекулы соседними частицами будут притягиваться в глубь сосуда. Причем, поправка давления будет прямо пропорциональ-на как числу притягиваемых, так и числу притягивающих молекул. Иначе говоря, она будет прямо пропорциональна квадрату их плотнос-ти. Отсюда можно записать
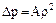 , (23)
, (23)
где ∆p - поправка на давление, учитывающая силы взаимодействия между молекулами;
А - коэффициент пропорциональности, принимающий для каждого
газа определенное числовое значение, не зависящее от параметров состояния;
ρ - плотность газа.
Введя вторую поправку в уравнение (6), имеем
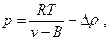
или
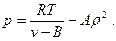 (24)
(24)
Учитывая, что произведение плотности на удельный объем равно единице, уравнение (9) можно записать следующим образом:
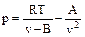 (25)
(25)
Отсюда уравнение Ван-дер-Ваальса принимает вид
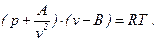 (26)
(26)
Это уравнение было опубликовано Ван-дер-Ваальсом в 1873 г.
Величину 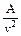 называют внутренним давлением, для жидкостей оно принимает очень большое значение (для воды при T=293 K оно составляет примерно 10800 бар), для газов оно сравнительно невелико и зависит от давления и температуры газа.
называют внутренним давлением, для жидкостей оно принимает очень большое значение (для воды при T=293 K оно составляет примерно 10800 бар), для газов оно сравнительно невелико и зависит от давления и температуры газа.
Уравнение Ван-дер-Ваальса качественно отображает поведение реальных веществ в жидком или газообразном состоянии. Для двухфазных состояний оно неприменимо.
Вопросы для самопроверки
1 Чем отличаются реальные газы от идеальных?
2 Что называется коэффициентом сжимаемости?
3 Как в уравнении Ван-дер-Ваальса учитывается наличие собственного объема молекул?
4 Как в уравнении Ван-дер-Ваальса учитывается наличие сил взаимодействия между молекулами?
5 Какая величина называется внутренним давлением?
6 Для каких состояний рабочего тела применимо это уравнение?
Водяной пар
Основные понятия и определения
Водяной пар широко используется в энергетике, отоплении, для различных технических нужд. Он является рабочим телом в тепловых двигателях (паровых поршневых машинах, паротурбинных установках), а также в различных нагревательных устройствах (теплообменных аппаратах, в нагревательных приборах парового отопления, в калориферах и т. д.), где он используется в качестве теплоносителя.
Процесс парообразования может осуществляться двумя различными по интенсивности и характеру процессами:
1. Испарение – процесс парообразования с поверхности жидкости. Здесь при хаотическом тепловом движении отдельные молекулы, обладающие наибольшей скоростью, преодолевают поверхностное натяжение и вылетают в пространство над поверхностью раздела. Испарение может быть полным, если над жидкостью – неограниченное пространство.
2. Кипение – процесс одновременного и многократного испарения жидкости в область, образованную паровым пузырьком.
Для возникновения кипения температура жидкости должна несколько превышать температуру кипения при данном давлении, т.е. должен быть местный перегрев этой жидкости. При отводе тепла от пара он будет вновь превращаться в жидкость. Этот обратный процесс называется конденсацией. Процесс кипения, так же как и процесс конденсации, протекает при постоянной температуре, если при этом давление рабочего тела не меняется. Жидкость, полученную при конденсации пара, называют конденсатом.
Полученные пары бывают насыщенными и перегретыми.
Насыщенный пар получается в том случае, если в закрытом сосуде наступает момент, когда количество молекул, вылетающих из жидкости, равно числу молекул, возвращающихся обратно в жидкость. Пар в этом состоянии принимает максимальную плотность при данной температуре. То есть, можно сказать, что насыщенный пар – это пар, соприкасающийся с жидкостью и находящийся с ней в термическом равновесии. С изменением температуры равновесие нарушается, вызывая изменение плотности и давления насыщения.
Насыщенные пары, в свою очередь, можно разделить на 2 группы:
1) сухие насыщенные пары;
2) влажные насыщенные пары.
Сухой насыщенный пар получается в результате законченного парообразования, т.е. когда последняя капля жидкости перешла в пар. Это состояние рабочего тела является неустойчивым, т.к. при отводе тепла (или повышении температуры, или повышении давления) часть пара сконденсируется, и рабочее тело будет состоять из смеси пара с жидкостью. Такой пар будет называться влажным насыщенным. Влажный пар может рассматриваться как смесь сухого пара с мельчайшими капельками воды, взвешенными в паре. Его состав определяется степенью сухости x, которая представляет собой долю сухого пара во влажном. Следовательно, (1-х) – влажность пара. (Например, если степень сухости влажного пара х=0,75, то следует, что в рабочем теле 75% сухого пара и 25% - воды).
При незначительном повышении температуры или понижении давления сухой насыщенный пар переходит в состояние перегретого пара, отсюда при одном и том же давлении температура и объем перегретого пара будет больше соответствующих величин сухого пара. Чем больше степень перегрева, тем больше по своим термическим свойствам перегретый пар приближается к идеальному газу. Напротив, при приближении к состоянию насыщения все больше проявляется влияние конечного объема молекул и Ван-дер-Ваальсовых сил.
Пар различного состояния в промышленных условиях получается в паровых котлах (парогенераторах). Процесс парообразования протекает при постоянном давлении, т.е. является изобарным.
Как уже отмечалось, процесс производства пара идет при постоянном давлении. Он включает в себя три последовательных этапа:
- подогрев воды до температуры кипения (она еще называется температурой насыщения и обозначается Ts);
- парообразование, т.е. превращение кипящей жидкости в сухой насыщенный пар;
- перегрев пара до необходимой температуры.
Процесс парообразования в p−ν диаграмме
Диаграмма p-v процесса парообразования строится на основании экспериментальных данных. Проводятся процессы парообразования при различных давлениях (p1, p2, p3 и т.д.), при этом фиксируются состояния воды при температуре насыщения (на диаграмме они обозначаются точками b1, b2, b3 и т.д.). Точками c1, c2, c3 и т.д. фиксируются состояния сухого насыщенного пара для рассматриваемых давлений, а точками d1, d2, d3 и т.д. фиксируются состояния перегретого пара (рисунок 1). Начальное состояние воды на диаграмме обозначается точками a1, a2, a3 и т.д.

Соединяются точки a1, a2, a3 между собой, точки b1, b2, b3 между собой и точки c1, c2, c3 между собой. При этом на диаграмме получаются три характерные линии.
Линия I – соответствует состояниям воды при начальной температуре и различных давлениях.
Линия II – геометрическое место точек, характеризующих состояние воды при температуре насыщения Ts и различных давлениях. Она называется нижняя пограничная кривая. В любой ее точке у рабочего тела степень сухости равна нулю (х=0).
Линия III – геометрическое место точек, характеризующих состояние сухого насыщенного пара. В любой ее точке у рабочего тела степень сухости равна единице (х=1). Она называется верхняя пограничная кривая.
Линии II и III сходятся в одной точке (К), которая называется критической точкой. Она соответствует некоторому предельному критическому состоянию вещества, при котором исчезают различия между жидкостью и паром. Все параметры, относящиеся к этой точке, называются критическими. Для воды они имеют следующие значения:
pкр=22,06 МПа ;
tкр=374,15°С ;
vкр=0,00326 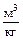 .
.
Между линиями I и II располагается область жидкости, которая нагревается от t=0°C до ts. Между линиями II и III – область влажного насыщенного пара. В этой области можно провести огромное количество линий, соответствующих определенной постоянной степени сухости х. Эти линии получили название линии сухости, они располагаются веерообразно от критической точки К.
Рассматриваемая диаграмма позволяет анализировать процесс кипения при различных давлениях и определять соответствующие параметры рабочего тела.
Вопросы для самопроверки
1 Какой процесс называется испарением?
2 Какой процесс называется кипением?
3 Какой пар называется влажным?
4 Какой пар называется сухим насыщенным?
5 Какой пар называется сухим перегретым?
6 Что характеризует степень сухости влажного пара?
7 Чем характерна критическая точка?
8 Какая линия на диаграмме p-v называется нижней пограничной кривой?
9 Какая линия на диаграмме p-v называется верхней пограничной кривой?
Дата: 2019-02-02, просмотров: 507.