Этот цикл описывает работу двигателей, использующих лёгкие топлива и имеющих искровое зажигание. В них время сгорания топлива очень мало, поэтому в термодинамической постановке вопроса теплоподвод считают происходящим при постоянном объёме. Иначе говоря, реальный процесс горения топлива заменяют идеальным процессом подвода тепла при постоянном объёме.

Изобразим в P-V и T-S диаграммах этот цикл (рисунок 2).

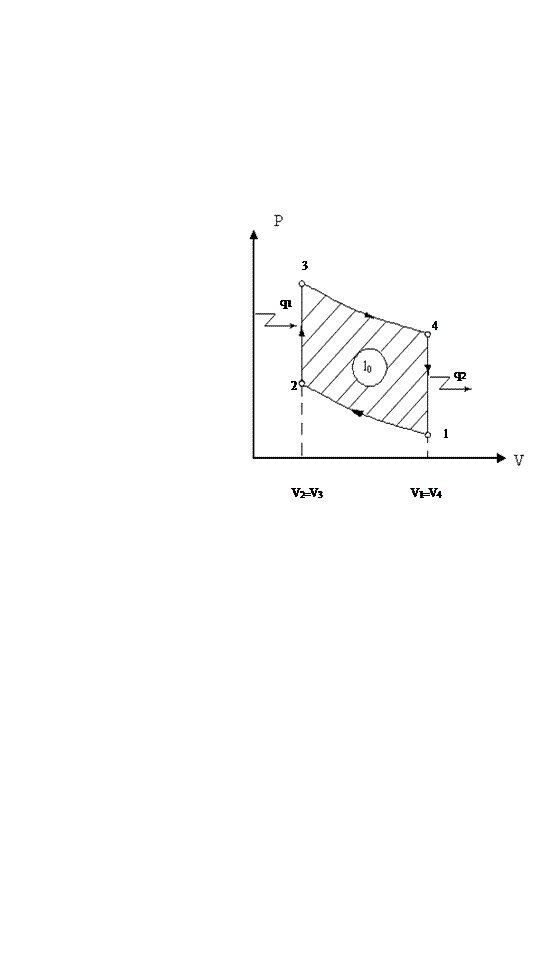
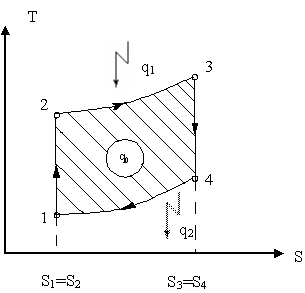
Рисунок 2 – изображение цикл ДВС с изохорным подводом тепла.

Рассмотрим процессы, из которых составлен этот цикл.

Процесс 1-2 – адиабатное сжатие рабочего тела.

Процесс 2-3 – изохорный подвод тепла.

Процесс 3-4 – адиабатное расширение рабочего тела.

Процесс 4-1 – изохорный отвод тепла.

Основными характеристиками цикла являются степень сжатия 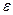 и степень повышения давления .

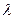Под степенью сжатия понимается отношение объёмов рабочего тела в процессе 1-2 (рисунок 2)

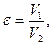                                                                                (8)

где 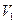 – объём рабочего тела в первоначальном состоянии;

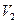 – объём рабочего тела в результате его адиабатного сжатия.

Под степенью повышения давления 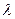 понимается отношение давлений рабочего тела в процессе 2-3 (рисунок 2)

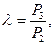                                                                                                (9)

где 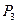 – удельное давление рабочего тела в точке 3;  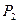– удельное давление рабочего тела в точке 2.

Получим выражение для расчёта термического к.п.д. данного цикла при условии, что нам известны основные параметры т.1 и характеристики цикла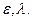

Запишем выражение термического к.п.д., используя формулу (6)

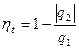                                                                        (10)

Выразим указанные количества тепла. Подведённая теплота 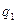 вычисляется по формуле:

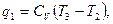                                                                          (11)

где 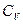– теплоёмкость рабочего тела в изохорном процессе;

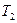 – начальная температура рабочего тела в процессе 2-3;

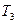– конечная температура рабочего тела в процессе 2-3.

Поскольку теплота отводится также в изохорном процессе, то она будет равна

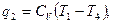                                                                              (12)

где 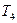 – начальная температура рабочего тела в процессе 4-1;

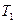 – конечная температура рабочего тела в процессе 4-1.

Подставляя выражения 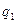и 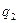 в формулу для термического к.п.д., будем иметь

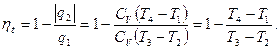                   (13)

Выразим температуры в характерных точках цикла через его параметры и начальную температуру .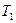

Определяем 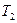, для этого рассматриваем процесс 1-2. это адиабатный процесс, т.е. 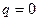. Запишем соотношение между параметрами рабочего тела данного процесса

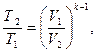                                                                                (14)

где 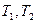 – начальная и конечная температура рабочего тела;

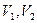– начальный и конечный объём рабочего тела;

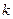  – показатель адиабаты.

Так как 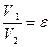, то выражение (14) принимает вид

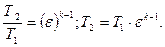                                                           (15)

Выражаем температуру T₃ через известные величины, для этого рассматриваем процесс 2-3, он – изохорный, поэтому соотношения между параметрами имеет вид

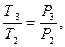                                                                                           (16)

где 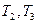 – начальная и конечная температура рабочего тела в процессе;

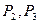– начальное и конечное удельное давление рабочего тела в процессе.

Отсюда

                                           .

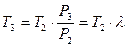Подставляя вместо T₂ выражение (15), будем иметь

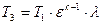                                           .                                        (18)

Выражаем температуру T₄ через известные величины. Рассматриваем процесс 3-4, который является адиабатным. Используя соотношения между параметрами для адиабатного процесса (14), можем записать

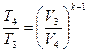                                             .                                      (19)

Но так как V₄=V₁; V₃=V₂, то подставляя в (19), получим

                           .

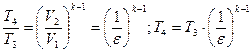Отсюда, подставляя вместо T₃ выражение (18), имеем

                           .

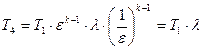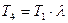                                           .                                                   (19)

Полученные выражения для 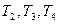 подставляем в (13) и произведём ряд математических операций

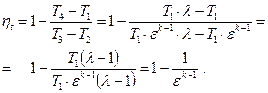
Таким образом, полученное выражение для расчёта термического к.п.д. цикла с изохорным подводом тепла имеет вид

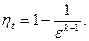                                                                                    (22)

Из выражения (22) видно, что 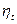 зависит только от степени сжатия  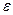и от природы рабочего тела. С увеличением  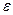и 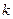 термический к.п.д. увеличивается. Однако, если при малых степенях сжатия повышение  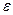вызывает существенное увеличение термического к.п.д., то при высоких значениях  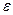возрастание  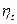при увеличении степени сжатия делается всё менее и менее значительным. В реальном же двигателе искрового зажигания выбор степени сжатия, в основном, определяется практическими возможностями организации процесса сгорания топлива без детонации (т.е. без самовоспламенения топлива).