Треугольный элемент с тремя узлами широко используется для решения двумерных задач теплопроводности.
Уравнение теплопроводности в сплошной среде (2.56), рассмотренное в предыдущей главе, имеет вид:
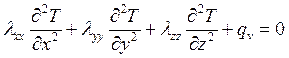
Где Т – температура;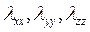 
- коэффициенты теплопроводности в направлениях x, y и z размерности кВт/м*К; 
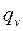- источник тепла внутри тела, который считается положительным, если тепло подводится к телу, его размерность кВт/м3.
Так как мы рассматриваем двумерную задачу, то уравнение теплопроводности примет вид:
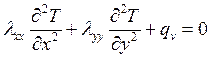(2.90)
Запишем уравнение теплопроводности для одномерной задачи в следующем виде:
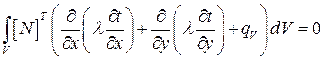(2.91)
Где [N]Т – матрица, содержащая функцию формы.
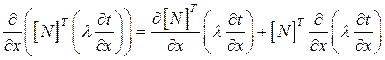(2.92)
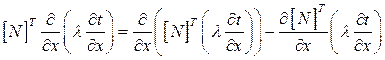(2.93)
Аналогично получаем для производной по y.
Используя теорему Остроградского-Гаусса, перейдем от интеграла по объему к замкнутой поверхности:
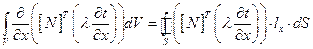(2.94)
Аналогично для компоненты у:
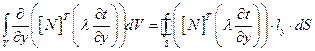(2.95)
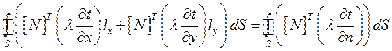(2.96)
Используя выражения для площади и объема, запишем:
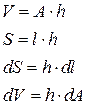
Где V – объем элемента; S – площадь боковой поверхности; h – толщина элемента, которая предполагается постоянной и единичной; А – площадь поверхности.
Заменим dV на dA, используя уравнения представленные выше:
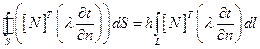(2.97)
В результате выражение (2.91) примет вид:
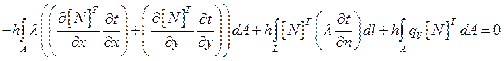(2.98)
Запишем выражения для граничных условий:
ГУ 2 рода: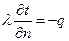 
(2.99)
ГУ 3 рода: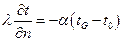 
(2.100)
Используя выражения (2.99) и (2.100) запишем:
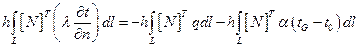(2.84)
Уравнения для температуры внутри элемента:
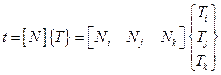(2.101)
Рис. 2.16. Треугольный элемент
Запишем уравнение теплопроводности, используя (2.101):
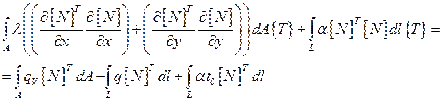(2.102)
Таким образом, результирующая система уравнений имеет вид:
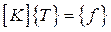(2.103)
Где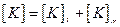 
– матрица жесткость (теплопроводности);
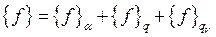- вектор столбец.
Суммируя эти уравнения для каждого элемента, получим:
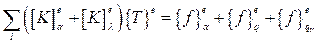(2.104)
Матрица коэффициентов, учитывающая теплообмен:
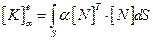(2.105)
Матрица коэффициентов, учитывающая теплопроводность:
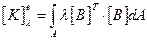(2.106)
Вектор столбец, учитывающий конвективный теплообмен:
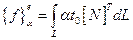(2.107)
Вектор столбец, учитывающий поток тепла:
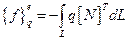(2.108)
Вектор столбец, учитывающий внутренние источники тепла:
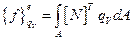(2.109)
Где [B] – матрица градиентов.
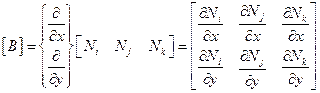(2.110)
Функции формы для линейного треугольного элемента:
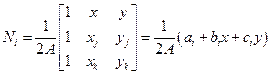(2.111)
Где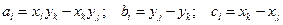 
Функции формы для узлов j и k получаются аналогично. Значения коэффициентов находятся следующим образом:
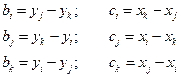
Запишем матрицу градиентов:
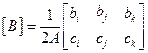(2.112)
И матрицу свойств материала:
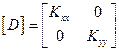(2.112)
Так как свойства материала в данной задаче одинаковы во всех направлениях, то матрица свойств заменяется коэффициентом теплопроводности.
Вычислим матрицу теплопроводности элемента:
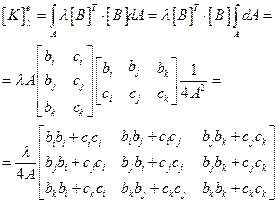(2.113)
Коэффициент, учитывающий конвективный теплообмен должен быть вычислен по поверхности. Подставляя в матрицу [N] функции формы и выполняя матричное умножение, получаем:
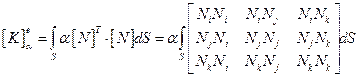(2.114)
Функции формы зависят от x и y, поэтому произведения вида NiNj не могут быть вынесены за знак интеграла. Кроме того, значение интеграла зависит от того, на какой поверхности наблюдается конвективный теплообмен.
Рис 2.17. Конвективные потери тепла вдоль одной из сторон элемента.
Если, например, конвекции подвержена сторона между узлами i и j (рис 2.17), то Nk равно нулю вдоль этой стороны и интеграл сводится к следующему выражению:
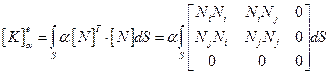(2.115)
Если любая из двух сторон подвержена конвекции, то расположение отличных от нуля членов в (2.114) будет иным, чем в (2.115).
Вычисление произведений в (2.114) не представляет труда, если применить L – координаты. Предполагая, что L 1 измеряется от стороны, противоположной i-му узлу, можно записать:
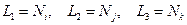
Если предположить, что конвективный теплообмен имеет место на повести стороны элемента между узлами i и j, то в точках этой поверхности Nk=L 3=0 и соотношение (2.115) примет вид:
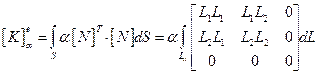(2.116)
где dS=tdL, причем толщина t предполагается единичной. Два типа произведений входят в формулу (2.116): квадрат величины L 1 2 или L 2 2 и перекрестное произведение L 1 L 2. Начнем с квадратных членов:
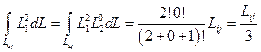
где Lij – длина стороны между узлами i и j. Интегрирование перекрестного произведения дает
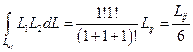
Интегралы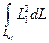 
и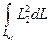 
равны между собой. Подставляя полученные результаты в формулу (2.116), получаем
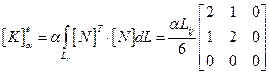(2.117)
Аналогичные соотношения получаются для стороны между узлами j и k:
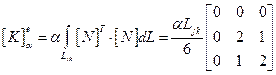(2.118)
и для стороны между узлами k и i:
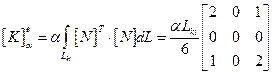(2.119)
Три интеграла в выражении для вектора нагрузки элемента также легко вычисляются, если воспользоваться L – координатами. Начнем с интеграла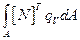 
; предположим, что величина Q постоянна внутри элемента. Тогда будем иметь:
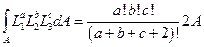
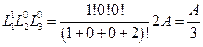
Тогда выражение для вектора нагрузки будет иметь вид:
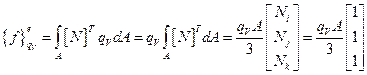(2.120)
Таким образом, тепло, генерируемое в элементе, распределяется поровну по трем узлам. Интегралы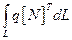 
и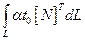 
записываются в одинаковой форме. Эти интегралы можно рассмотреть так же как (2.114). Результаты зависят от того, на какой из сторон элемента происходит конвективный теплообмен, характеризуемый величиной α, или приток тепла за счет теплового потока q.
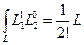
Предполагая q постоянным по поверхности элемента, получим три следующие формы записи:
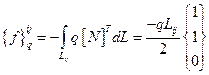(2.121)
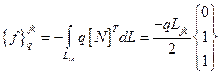(2.122)
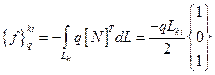(2.123)
Величина 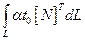идентична (2.121) - (2.123) с учетом замены q на α t 0.
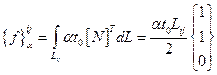(2.124)
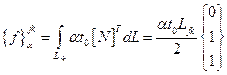(2.125)
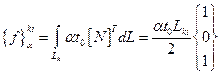(2.126)
Если тепловой поток или конвективный теплообмен наблюдается на двух сторонах элемента, то поверхностный интеграл заменяется суммой интегралов по каждой из сторон. Тоже самое относится к интегралу (2.114)
ПРИМЕР №2
Ниже изображен элемент, который использован для дискретизации сплошной среды. По двум поверхностям этого элемента происходит конвективный теплообмен. Указаны размеры элемента и физические характеристики. Требуется составить матрицы элемента, предполагая его толщину единичной.
Рис. 2.18. Пример №2
Рассмотрим матрицу теплопроводности элемента:
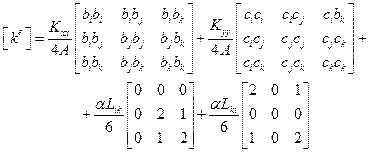
Константы b и c вычисляются по формулам:
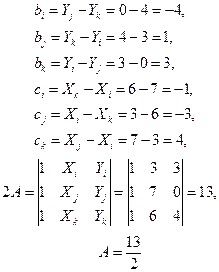
Длины сторон Ljk и Lki равны:
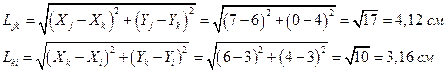
Подстановка полученных числовых значений в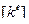 
дает:
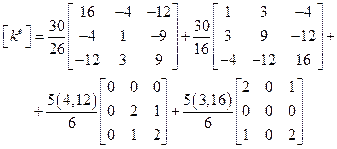
или
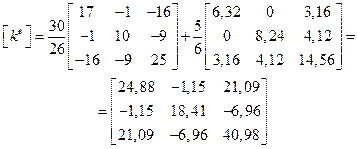
Вектор нагрузки элемента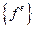 
представляет собой сумму двух поверхностных интегралов по каждой из сторон, где происходит конвективный теплообмен:
Дата: 2019-02-02, просмотров: 213.
