Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Уравнение теплопроводности в сплошной среде имеет вид:

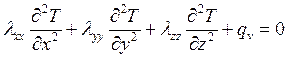           (2.56)

Где Т – температура; 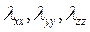 - коэффициенты теплопроводности в направлениях x, y и z размерности кВт/м*К;  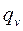- источник тепла внутри тела, который считается положительным, если тепло подводится к телу, его размерность кВт/м³.

Так как мы рассматриваем одномерную задачу, то уравнение теплопроводности примет вид:

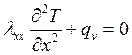                           (2.57)

Перенос тепла осуществляется вдоль стержня. На боковых поверхностях заданы адиабатические условия или теплопроводность плоской стенки. На левой и правой границе задаются граничные условия 1,2 или 3 рода.

С уравнением (2.56) связывают два различных типа граничных условий. Если температура известна на некоторой части границы, то записывают:

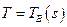,                          (2.58)

Где Т_В – температура на границе, которая может быть функцией координат точек поверхности s. Если на границе происходит конвективный теплообмен, который характеризуется величиной h( T- T₀), или задан поток тепла q, то граничное условие имеет вид:

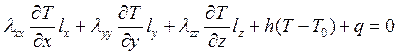         (2.59)

Где h -  коэффициент теплообмена, кВт/м²*К; Т – температура на границе (неизвестная), К; Т₀ – температура окружающей среды (известная), К; l_x, l_y и l_z – направляющие косинусы; q - поток тепла кВт/м², который считается положительным, если тепло теряется телом. Поток тепла q и конвективная потеря тепла h( T- T₀) не имеют места на одном и том же участке поверхности границы. Если существуют потери тепла за счет конвекции, то отсутствует отвод или приток тепла за счет теплового потока и обратно.

Уравнения (2.56) и (2.59) могут быть применены к одномерным и двумерным задачам после простого вычеркивания членов, связанных с ненужными координатами. Уравнение для одномерной задачи с граничными условиями запишется в виде:

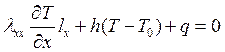                  (2.60)

Если конвективный теплообмен отсутствует, кроме того, поток тепла равен нулю, то уравнение (2.59) сводится к соотношению:

     

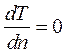
Которое выражает условие существования теплоизолированной границы (n – внешняя нормаль).

Запишем уравнение теплопроводности для одномерной задачи в следующем виде:

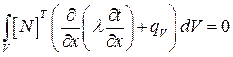                        (2.61)

Где [N]^Т – матрица, содержащая функцию формы.

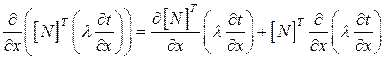            (2.62)

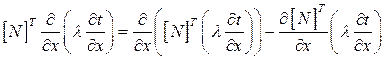            (2.63)

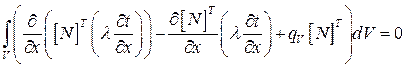        (2.64)

Используя теорему Остроградского-Гаусса, перейдем от интеграла по V к замкнутой поверхности:

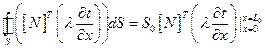                           (2.65)

На левой границе задаем ГУ 2 рода, а на правой – 3 рода:

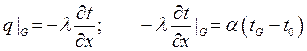
В результате с граничными условиями уравнение теплопроводности будет записано в виде:

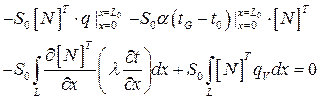                                (2.66)

Помножим полученное выражение на 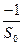  и используя выражение t=[N]{T} запишем уравнение теплопроводности:

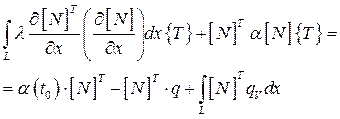               (2.67)

Таким образом, результирующая система уравнений имеет вид:

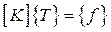                                       (2.68)

Где 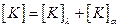 – матрица жесткость (теплопроводности);

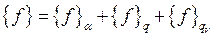- вектор столбец.

Суммируя эти уравнения для каждого элемента, получим:

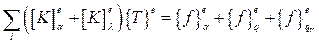                                (2.69)

Интерполяционный полином для одномерного линейного элемента имеет вид:

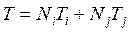                                   (2.70)

Где 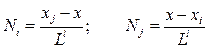 - функции формы, которые определены относительно системы координат, показанной на рис. 2.14

 

 

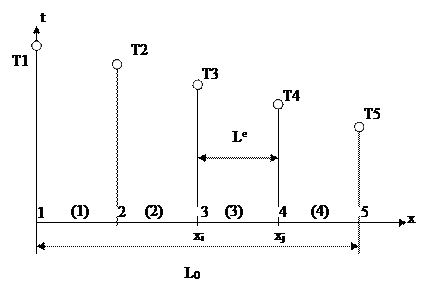Рис. 2.14 Система координат, относительно которой определены функции формы.

 

Матрица жесткости элемента получается суммированием матриц 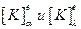, а вектор столбец – сложением матриц 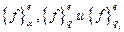. Рассмотрим составляющие матриц подробнее.

Матрица коэффициентов, учитывающая теплообмен:

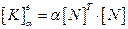                                   (2.71)

Матрица коэффициентов, учитывающая теплопроводность:

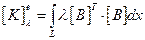                                (2.72)

Вектор столбец, учитывающий конвективный теплообмен:

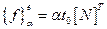                                       (2.73)

Вектор столбец, учитывающий поток тепла:

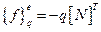                                         (2.74)

Вектор столбец, учитывающий внутренние источники тепла:

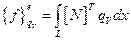                                   (2.75)

Матрица градиентов 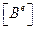 получается дифференцированием  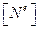по x:

 

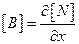
Матрица свойств элемента сводится к одному коэффициенту, так как свойства внутри элемента постоянны:

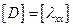                                              (2.76)

Вычислим интегралы из (2.69):

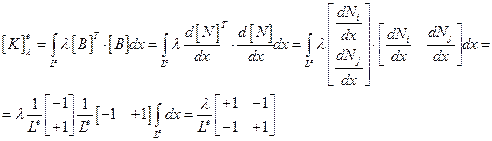(2.77)

 

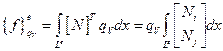                          (2.78)

Так как 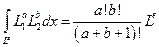, то интеграл от N_i по dx иметь вид:

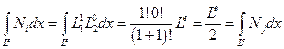                       (2.79)

Тогда, используя (2.79), выражение (2.78) примет вид:

 

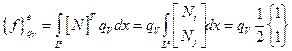                     (2.80)

Выражение для коэффициента, учитывающего теплообмен примет вид:

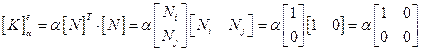     (2.81)

Выражение для коэффициентов и вектор столбца запишется следующим образом:

Если заданы на правой стороне:

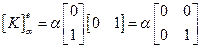                              (2.82)

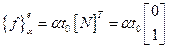                                    (2.83)

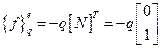                                      (2.84)

Если на левой стороне:

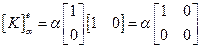                              (2.85)

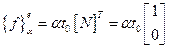                                    (2.86)

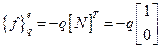                                      (2.87)

Суммируя все коэффициенты и вектор столбцы, получим общее выражение для узла:

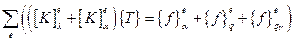                     (2.88)

Выражение (2.88) запишется в сокращенном виде:

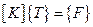                                                                              (2.89)

ПРИМЕР №1

Требуется вычислить распределение температуры в одномерном стержне с приведенными ниже физическими характеристиками.

Разделим конструкцию на 5 элементов длинной 1,5 см каждый. Матрицы элементов для первых четырех элементов идентичны и могут быть составлены с помощью формул:

 

 

 

 

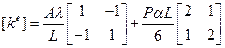
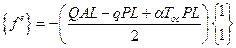
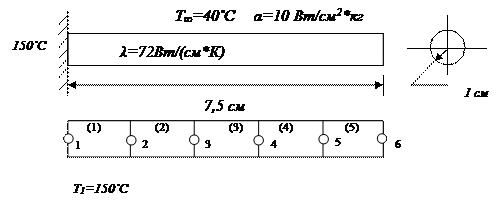Рис. 2.15 Пример №1

 

Запишем величины различных параметров, входящих в эти соотношения:

 

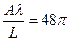
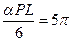
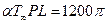
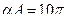
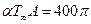
Матрица теплопроводности для первого элемента имеет вид

                         

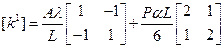
или

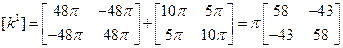
Матрица теплопроводности для второго, третьего и четвертого элемента идентичны 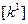. Вектор нагрузки элемента преобразуется к виду:

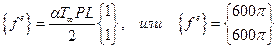
так как Q и q равны нулю

Матрицы для пятого элемента получаются из соответствующих матриц первого элемента добавлением членов, описывающих потери тепла на правом конце стержня. Чтобы построить матрицу теплопроводности, нужно добавить к 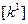результаты вычислений (2.81). Так как αА=10π, нужно добавить следующую матрицу:

                                

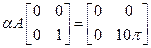
и

                     

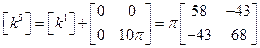
Вектор нагрузки для пятого элемента

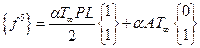
или

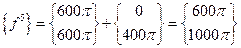
После применения метода прямой жесткости совокупность рассмотренных матриц элементов приводит к следующей системе уравнений:

              

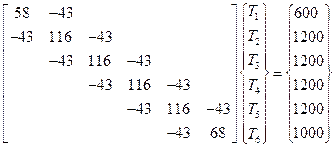
Здесь проведено сокращение на множитель π, так как он входит в обе части системы уравнений. Пустые места в [k] означают нулевые коэффициенты.

Значение Т₁ известно (150˚С), так что система уравнений должна быть модифицирована перед решением. Эта модификация преобразует стобец правых частей к виду

               

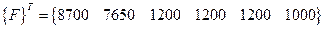
После решения системы имеем

                  

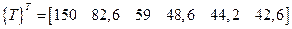
Теоретические значения температуры [2] следующие:

              

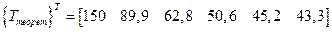
Результаты, полученные по методу конечных элементов, достаточно хорошо согласуются с истинными значениями, если учесть, что было проведено разбиение области на одинаковые элементы. Решение по методу конечных элементов можно было бы улучшить, если использовать более короткие элементы вблизи стены, в которую заделан стержень.