Четырехугольный элемент представляет собой мультиплекс-элемент. Границы такого элемента должны быть параллельны координатным линям для сохранения непрерывности при переходе от одного элемента к другому. Прямоугольный элемент является специальным случаем четырехугольника. Свойства прямоугольного элемента служат основой для применения криволинейной системы координат, необходимой при использовании четырехугольного элемента.
Интерполяционный полином для прямоугольного элемента с четырьмя узлами имеет вид
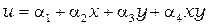 , (2.35)
, (2.35)
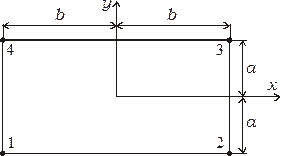
Рис. 2.10. Прямоугольный элемент
Пронумерованные узлы и расположение системы координат показаны на рис. 210. В узлах должны быть выполнены следующие условия
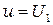 при
при 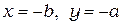 ,
,
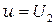 при
при 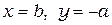 ,
,
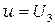 при
при 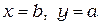 ,
,
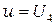 при
при 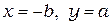 .
.
Подстановка этих выражений в формулу (2.35) приводит к системе четырех уравнений, которые могут быть решены относительно коэффициентов полинома (2.35) 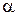
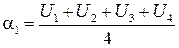 ,
,
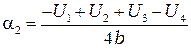 ,
,
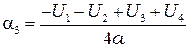 ,
,
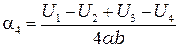 .
.
Подставим 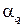 (
( 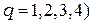 в исходное соотношение и преобразуем его к виду
в исходное соотношение и преобразуем его к виду
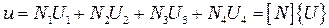 , (2.35)
, (2.35)
где 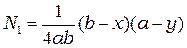 ,
, 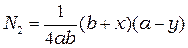 ,
, 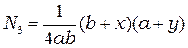 ,
, 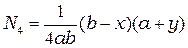 .
.
Одно из главных различий между этим элементом и симплекс-элементами состоит в том, что градиенты теперь не постоянны, а меняются линейно вдоль одного из координатных направлений. Например,
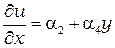 и
и 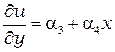 .
.
Градиент в направлении оси 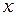 постоянен вдоль оси
постоянен вдоль оси 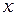 , но меняется линейно по
, но меняется линейно по 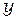 , и, наоборот,
, и, наоборот, 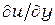 постоянен по
постоянен по 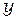 , но линейно изменятся вдоль оси
, но линейно изменятся вдоль оси 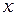 .
.
Полученные результаты для прямоугольного элемента могут быть записаны в безразмерной форме с помощью отношений 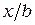 и
и 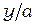 . Тогда
. Тогда
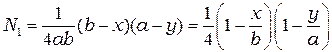 ,
,
где 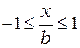 и
и 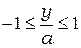 .
.
Если обозначить эти отношения как
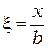 и
и 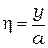 , (2.36)
, (2.36)
То функции формы в соотношении (2.35) могут быть представлены в виде произведений безразмерных координат
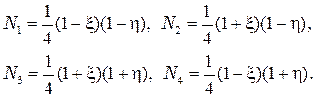 (2.37)
(2.37)
Элемент с локальными координатами 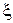 и
и 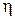 показан на рис. 2.11.
показан на рис. 2.11.

Рис. 2.11. Система координат 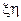 для
для
прямоугольного элемента
Введенная система координат называется естественной (локальной). Естественная система координат может быть криволинейной. Использование криволинейной системы координат позволяется изменять ориентацию сторон четырехугольника относительно системы координат 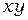 . На рис. 2.12 показан четырехугольный элемент общего вида. Началу координат соответствует точка пересечения двух линий делящих пополам противоположные стороны элемента (штриховые линии на рис. 2.12). Линия, соответствующая
. На рис. 2.12 показан четырехугольный элемент общего вида. Началу координат соответствует точка пересечения двух линий делящих пополам противоположные стороны элемента (штриховые линии на рис. 2.12). Линия, соответствующая 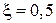 , также показана на рис. 2.12. Эта линия не параллельна оси.
, также показана на рис. 2.12. Эта линия не параллельна оси.
Функции формы для элемента, показанного на рис. 2.12, идентичны функциям формы, представленным формулами (2.37). Необходимо отметить, что теперь нельзя непосредственно получить частные производные 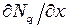 и
и 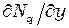 . Необходимы формулы преобразования координат, чтобы связать систему
. Необходимы формулы преобразования координат, чтобы связать систему 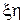 с системой
с системой 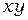 .
.
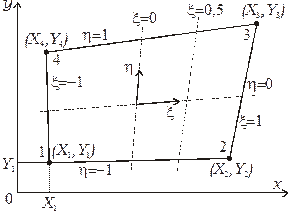
Рис. 2.12. Четырехугольный элемент
Поскольку элементные вклады содержат, как убедимся позже, декартовы производные, необходимо преобразовать производные по 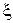 и
и 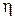 в производные
в производные 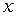 и
и 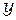 . Общее преобразование имеет вид
. Общее преобразование имеет вид
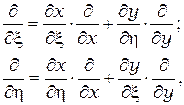 (2.37)
(2.37)
Или в матричной форме
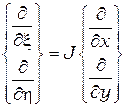 ,
, 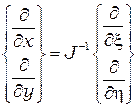 , (2.38)
, (2.38)
где 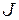 есть якобиан преобразования координат
есть якобиан преобразования координат
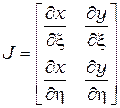 , (2.39)
, (2.39)
а обратный якобиан определяется по формуле
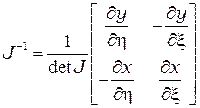 , (2.40)
, (2.40)
здесь 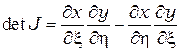 – определить якобиана
– определить якобиана 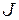 .
.
Как было показано выше, связь между координатами 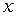 ,
, 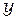 и
и 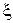 ,
, 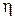 с началом координат в центре прямоугольного элемента (см. рис. 2.10) определяются соотношениями (2.36).
с началом координат в центре прямоугольного элемента (см. рис. 2.10) определяются соотношениями (2.36).
Для произвольного четырехугольного элемента, показанного на рис. 2.12 связь между координатами 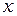 ,
, 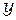 и
и 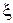 ,
, 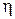 определятся уравнениями
определятся уравнениями
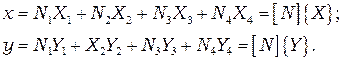 , (2.41)
, (2.41)
Здесь: 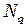 (
( 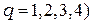 – функции формы описывают преобразование координат и определяются выражениями (2.37).
– функции формы описывают преобразование координат и определяются выражениями (2.37).
Необходимо отметить, что функция, описывающая преобразование координат, может не совпадать по порядку с интерполяционной функцией, что позволяет описывать геометрию элемента независимо от аппроксимации неизвестной величины. Это позволяет сочетать как интерполяционные полиномы высокого порядка с элементами простой геометрии, так и элементы сложной формы с простыми интерполяционными полиномами. Если форма конечного элемента описывается полиномами той же степени, что и базисные функции, то такой конечный элемент называется изопараметрическим. Если степень этих полиномов меньше, чем у базисных функций, то элемент называется субпараметрическим, в противоположном случае – суперпараметрическим [125]. Эту терминологию иногда трудно применить к аппроксимации МКЭ уравнений Навье-Стокса. Например, на шестиузловых квадратичных треугольных элементах используется квадратичная интерполяция для скорости (изопараметрический конечный элемент) и линейная для давления (суперпараметрический конечный элемент).
После подстановки в якобиан (2.39) уравнений (2.41) с учетом выражений для функции формы (2.37) получим
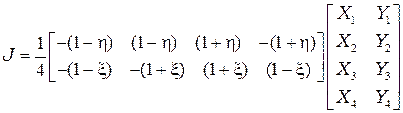 . (2.42)
. (2.42)
Дата: 2019-02-02, просмотров: 325.