Когда используется произвольная глобальная система координат, значения узловых координат ограничены только границами области. Было бы полезным упрощением, если бы экстремальные значения этих координат принимали значения –1, 0 или 1. Этого можно достигнуть выбором локальной (местной) системы координат, привязанной к элементу так, чтобы координаты менялись линейно между нормированными узловыми координатами. Система координат такого типа называется системой локальных (естественных) координат.
Преимущество естественных координат состоит в том, что интегрирование по элементу для метода конечных элементов часто может быть проведено в стандартном аналитическом виде.
Рассмотрим одномерный элемент 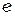 с узлами
с узлами 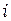 и
и 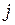 (см. рис. 2.8). Координатами узлов
(см. рис. 2.8). Координатами узлов 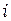 и
и 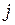 в глобальной системе координат являются
в глобальной системе координат являются  и
и 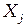 , соответственно.
, соответственно.
Введем локальную систему координат, поместив начало системы в 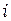 -м узле элемента (см. рис. 2.8)
-м узле элемента (см. рис. 2.8)
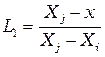 . (2.25)
. (2.25)
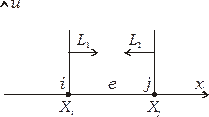
Рис. 2.8. Локальная система координат
для одномерного элемента
Для узла 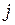 локальная система координат запишется
локальная система координат запишется
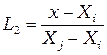 . (2.26)
. (2.26)
Из выражений (2.25), (2.26) видно, что при 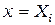 –
– 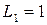 ,
, 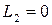 , а при
, а при 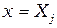 –
– 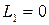 ,
, 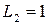 .
.
Независимой является только одно из координат 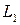 и
и 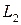 , что следует из соотношения
, что следует из соотношения  .
.
Можно отметить также, что 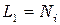 и
и 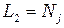 . Таким образом
. Таким образом
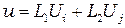 . (2.27)
. (2.27)
Как будет показано ниже, обычно элементные вклады могут быть выражены в 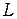 -координатах как произведение узловых значений и интегралов типа
-координатах как произведение узловых значений и интегралов типа 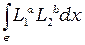 , где
, где 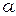 и
и 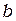 целочисленные показатели степени. Интегрирование можно провести аналитически согласно формуле
целочисленные показатели степени. Интегрирование можно провести аналитически согласно формуле
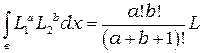 , (2.28)
, (2.28)
где 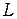 – длина конечного элемента.
– длина конечного элемента.
2.5. Локальная система координат для двухмерного симплекс-элемента
Координата площади в двухмерном случае аналогична координате длины в одномерном случае. Для произвольно выбранной точки 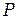 в трехузловом элементе площадь треугольника
в трехузловом элементе площадь треугольника 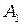 (см. рис. 2.9) определяется по формуле
(см. рис. 2.9) определяется по формуле 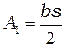 , а площадь всего треугольника
, а площадь всего треугольника 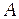 – по формуле
– по формуле 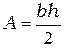 . Тогда отношение площадей
. Тогда отношение площадей
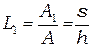 . (2.29)
. (2.29)
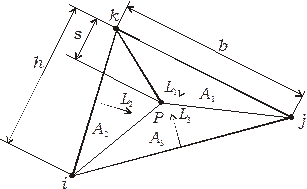
Рис. 2.9. Три площади, связанные с произвольной
точкой треугольника, и локальные координаты
Ясно, что величина 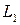 изменяется в пределах от нуля до единицы. Координаты
изменяется в пределах от нуля до единицы. Координаты 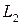 и
и 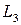 определяются аналогично
определяются аналогично
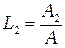 ,
,  , (2.30)
, (2.30)
и изменяются в тех же пределах, что и 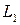 .
.
Так как  ,
,
 . (2.31)
. (2.31)
Координаты 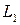 ,
, 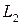 ,
, 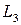 называются
называются 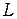 -координатами.
-координатами.
Изучение свойств 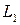 ,
, 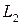 ,
, 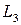 с учетом соотношения (2.31) обнаруживают некоторые интересные сведения. Координатные переменные
с учетом соотношения (2.31) обнаруживают некоторые интересные сведения. Координатные переменные 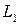 ,
, 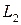 ,
, 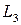 представляют собой функции формы для треугольного симплекс-элемента
представляют собой функции формы для треугольного симплекс-элемента
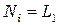 ,
, 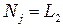 ,
, 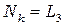 . (2.32)
. (2.32)
Как видно из рис. 2.9
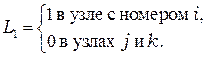
Подобные соотношения выполняются также для  и
и  . Кроме того, формула (2.31) позволяет утверждать, что в произвольной точке элемента функции формы всегда в сумме равны единице.
. Кроме того, формула (2.31) позволяет утверждать, что в произвольной точке элемента функции формы всегда в сумме равны единице.
Если записать следующие зависимости
 (2.33)
(2.33)
и разрешить их относительно 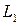 ,
, 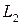 ,
, 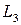 , то в результате получим соотношения, идентичные (2.22).
, то в результате получим соотношения, идентичные (2.22).
Формула интегрирования для треугольного симплекс-элемента с использованием 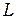 -координат имеет вид
-координат имеет вид
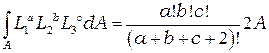 , (2.34)
, (2.34)
Использование соотношения (2.34) может быть проиллюстрировано при вычислении интеграла вида
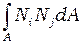
Этот интеграл по площади элемента преобразуется следующим образом
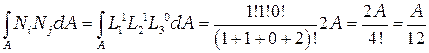
Дата: 2019-02-02, просмотров: 294.