ДИСКРЕТИЗАЦИЯ ОБЛАСТИ
На первом этапе конечноэлементной процедуры производится разбиение расчетной области на конечные элементы. Этот этап не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся навыков. Плохое или несовершенное разбиение может приводить к ошибочным результатам.
Дискретизация области включает: выбор формы элементов; задание их размеров и их количество; нумерацию элементов и узлов.
Типы конечных элементов
Размерность элемента определяется размерностью аппроксимируемой их совокупностью области определения задачи. Для соответствия элемента физической модели исследуемого объекта одномерный элемент может иметь поперечное сечение, площадь которого необязательно постоянна по длине элемента, а двухмерный элемент единичную толщину.
Простейший конечный элемент имеет число узлов больше на единицу мерности элемента и называется симплекс-элемент. Конечный элемент, имеющий большее число узлов, называется комплекс-элементом.
На рис. 2.1 приведены симплекс-элементы различной размерности.
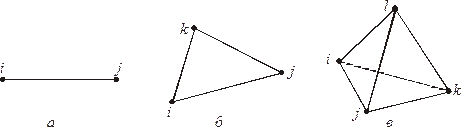
Рис. 2.1. Симплекс-элементы: а – одномерный;
б – двухмерный (треугольник); в – трехмерный (тетраэдр)
Симплекс-элементам соответствую полиномы, содержащие константу и линейные члены:
одномерный (см. рис. 2.1,а)
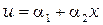 ; (2.1)
; (2.1)
двухмерный (см. рис. 2.1,б)
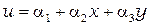 ; (2.2)
; (2.2)
трехмерный (см. рис. 2.1,в)
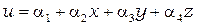 . (2.3)
. (2.3)
Нелинейные элементы высокого порядка, или комплекс-элементы должны иметь число узлов, равное числу коэффициентов в аппроксимирующем полиноме этого конечного элемента. Например, одномерный квадратичный элемент должен содержать три узла (см. рис. 2.2), т.к. его полином содержит три неизвестных коэффициента
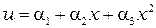 , (2.4)
, (2.4)
а кубический – четыре узла
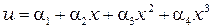 . (2.5)
. (2.5)
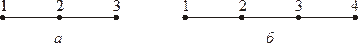
Рис. 2.2. Одномерные нелинейные элементы высокого порядка
а – квадратичный; б – кубический
Квадратичный треугольный элемент содержит шесть узлов (см. рис. 2.3), а полином – шесть коэффициентов
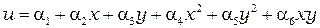 ; (2.6)
; (2.6)
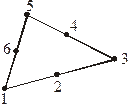
Рис. 2.3. Квадратичный треугольный элемент
Нелинейный двухмерный элемент с наименьшим числом узлов – это четырехугольник (см. рис. 2.4)
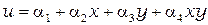 ; (2.7)
; (2.7)
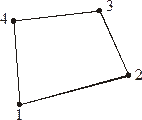
Рис. 2.4. Нелинейный четырехугольный элемент
Одномерный симплекс-элемент
Одномерный симплекс-элемент представляет собой прямолинейный отрезок длины 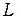 с двумя узлами, по одному, по одному на каждой стороне отрезка (см. рис. 2.5). Узлы обозначаются индексами
с двумя узлами, по одному, по одному на каждой стороне отрезка (см. рис. 2.5). Узлы обозначаются индексами 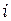 и
и 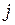 , узловые значения – через
, узловые значения – через 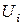 и
и 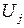 соответственно.
соответственно.
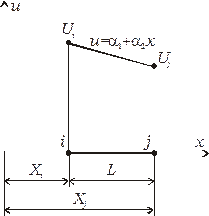
Рис. 2.5. Одномерный симплекс-элемент
Начало системы координат расположено вне элемента. Полиномиальная функция 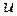 для скалярной величины имеет вид
для скалярной величины имеет вид
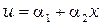 . (2.8)
. (2.8)
Здесь 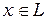 .
.
Коэффициенты полинома 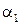 и
и 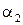 определяются через значения функции в узлах. В результате имеем систему из двух уравнений с двумя неизвестными
определяются через значения функции в узлах. В результате имеем систему из двух уравнений с двумя неизвестными
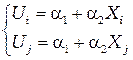 , (2.9)
, (2.9)
решение которой дает
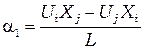 ,
, 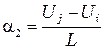 . (2.10)
. (2.10)
Подставляя найденные значения 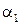 и
и 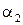 в формулу (2.8) получим
в формулу (2.8) получим
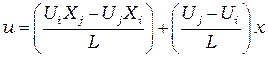 , (2.11)
, (2.11)
которое может быть переписано в виде
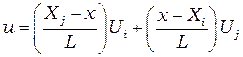 . (2.12)
. (2.12)
Линейные функции от 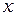 в формуле (2.12) называются функциями формы или интерполяционными функциями и обозначаются буквой
в формуле (2.12) называются функциями формы или интерполяционными функциями и обозначаются буквой 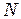
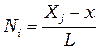 и
и 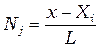 . (2.13)
. (2.13)
Как видно из формулы (2.13), функция 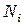 равна единице в узле с номером
равна единице в узле с номером 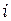 и равна нулю в узле
и равна нулю в узле 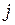 (см. рис. 2.6). Аналогично функция
(см. рис. 2.6). Аналогично функция 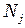 равна нулю в
равна нулю в 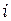 -м узле и равна единице в узле с номером
-м узле и равна единице в узле с номером 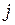 (см. рис. 2.6). Эти значения характерны для функций формы. Они равны единице в одном определенном узле и обращаются в нуль во всех других узлах.
(см. рис. 2.6). Эти значения характерны для функций формы. Они равны единице в одном определенном узле и обращаются в нуль во всех других узлах.
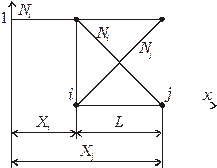
Рис. 2.6. Функции формы одномерного симплекс-элемента
Соотношение (2.12) может быть записано
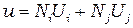 , (2.14)
, (2.14)
или в матричном виде
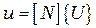 , (2.15)
, (2.15)
где 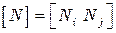 – матрица-строка функций формы конечного элемента (матрица функций формы);
– матрица-строка функций формы конечного элемента (матрица функций формы); 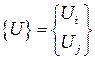 – вектор-столбец узловых значений функции
– вектор-столбец узловых значений функции 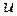 .
.
Выражение (2.15) является основополагающим и применимо к любым конечным элементам. Число элементов матриц 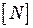 и
и 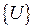 равно числу узлов конечного элемента. Для любой разновидности конечного элемента функция формы любого узла это функция заданная и непрерывная на конечном элементе и равная единице в этом узле и нулю во всех остальных узлах.
равно числу узлов конечного элемента. Для любой разновидности конечного элемента функция формы любого узла это функция заданная и непрерывная на конечном элементе и равная единице в этом узле и нулю во всех остальных узлах.
Двухмерный симплекс-элемент
Двухмерный симплекс-элемент показан на рис. 2.7.
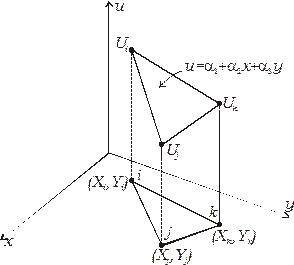
Рис. 2.7. Двухмерный симплекс-элемент
В методе конечных элементов принята нумерация узлов против часовой стрелки, начиная от некоторого 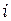 -го узла, который выбирается произвольно. Узловые значения скалярной величины
-го узла, который выбирается произвольно. Узловые значения скалярной величины 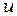 обозначаются через
обозначаются через 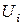 ,
, 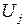 и
и 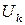 , а координатные пары трех узлов – через
, а координатные пары трех узлов – через 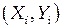 ,
, 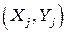 ,
, 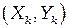 .
.
Интерполяционный полином имеет вид
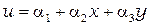 ; (2.16)
; (2.16)
Послед подстановки узловых значений функции 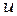 и соответствующих координат узлов получаем систему трёх уравнений
и соответствующих координат узлов получаем систему трёх уравнений
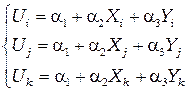 , (2.17)
, (2.17)
решая которую получаем
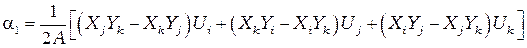 , (2.18)
, (2.18)
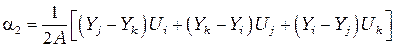 , (2.19)
, (2.19)
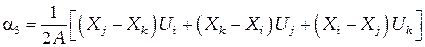 . (2.20)
. (2.20)
Определитель системы связан с площадью треугольника 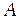 соотношением
соотношением
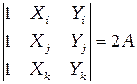 . (2.21)
. (2.21)
Выражения (2.18)–(2.20) можно записать в виде
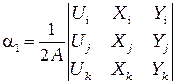 ,
, 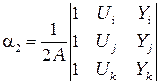 ,
, 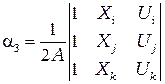
Подставляя значения 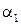 ,
, 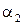 и
и 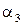 в формулу (2.16), можно преобразовать выражение для
в формулу (2.16), можно преобразовать выражение для 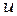 к виду, подобному (2.14). Это соотношение определяющее элемент, содержит три функции формы по одной для каждого узла:
к виду, подобному (2.14). Это соотношение определяющее элемент, содержит три функции формы по одной для каждого узла:
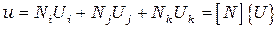 , (2.22)
, (2.22)
где 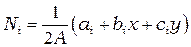 ;
; 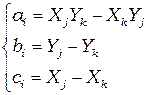 ; или
; или 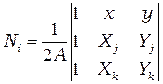 ;
;
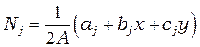 ;
; 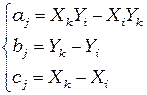 ; или
; или 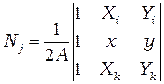 ;
;
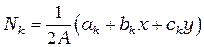 ;
; 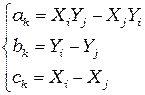 ; или
; или 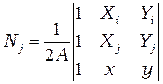 .
.
Значение функции формы 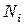 в
в 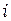 -м узле равно 1, а в узлах
-м узле равно 1, а в узлах 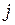 и
и 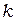 равно нулю. Аналогично функции
равно нулю. Аналогично функции 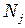 и
и 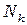 равны 1 соответственно в узлах
равны 1 соответственно в узлах 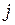 и
и 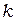 .
.
Скалярная величина 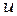 определяется внутри элемента функциями формы, линейными по
определяется внутри элемента функциями формы, линейными по 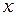 и
и 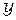 . Это означает, что градиенты этой величины в направлениях
. Это означает, что градиенты этой величины в направлениях 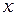 и
и 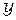 будут постоянны. Градиенты в направлении
будут постоянны. Градиенты в направлении 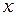 определяется соотношение
определяется соотношение
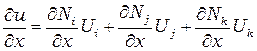 , (2.23)
, (2.23)
Поскольку
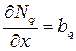 ,
, 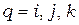 .
.
Поэтому
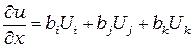 . (2.24)
. (2.24)
Так как 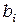 ,
, 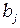 ,
, 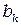 постоянны (они фиксированы как только заданы узловые координаты) и
постоянны (они фиксированы как только заданы узловые координаты) и 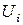 ,
, 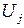 ,
, 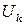 не зависят от координат пространства, частная производная в (2.24) имеет постоянное значение. Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию
не зависят от координат пространства, частная производная в (2.24) имеет постоянное значение. Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию 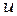 .
.
Пример
Требуется преобразовать следующую систему уравнений, если известно, что Т1=150 и Т5= 40:
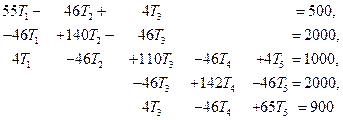
На первом этапе приравняем нулю все коэффициенты в первой и пятой строках, за исключением диагональных членов, которые оставим неизменными. Компоненты F 1 и F 5 в {F} заменим соответственно на K 11 T 1 и K 55 T 5. В результате будем иметь:
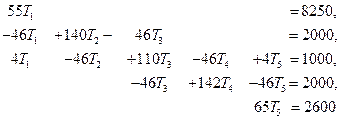
Второй этап состоит в исключении столбцов матрицы, коэффициенты которых умножаются на Т1 и Т5. Это осуществляется переносом членов, содержащих Т1 и Т5 в правую часть системы. Например, величина F2 становится равной 2000+46Т1, или 8900. Завершая второй шаг, получим:
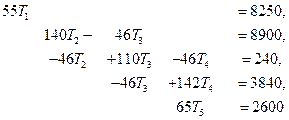
Описанная выше процедура совершенно проста и легко поддается программированию. Та же методика преобразования может быть использована также в случае, когда [K] хранится в виде прямоугольного массива. Логика программирования, однако, при этом более сложная.
Другой метод, применяемый некоторыми исследователями, состоит в том, что диагональный коэффициент, соответствующий заданному узловому значению Т β, умножается на очень большое число, скажем на 1015, а Fβ заменяется на (1015) Т β. Это равносильно приближенной замене коэффициентов вне главной диагонали нулям. Такой способ очень легко реализовать на ЭВМ, но он неприменим, если значение Т β очень мало. Именно с таким случаем сталкиваются при решении задач механики твердого деформируемого тела, когда заданные перемещения малы по величине. Первый метод, рассмотренный выше, всегда будет давать правильные результаты там, где мы сталкиваемся с малыми заданными величинами Т β.
Решение системы уравнений
Одним из наиболее эффективных методов решения системы уравнений, которые получаются при использовании метода конечных элементов, является известный вариант метода исключения Гаусса. Матрица системы преобразуется к треугольному виду, после чего решение получается обратной прогонкой. Проиллюстрируем сначала метод на примере решения простой системы уравнений, а затем проведем обобщение, обсуждая вопросы, которые имеют отношение к методу конечных элементов.
Рассмотрим систему уравнений:
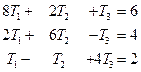 (2.48)
(2.48)
Матрица этой системы симметрична, причем наибольшие ее коэффициенты расположены на главной диагонали. Метод исключения основан на том, что любая неизвестная может быть исключена из всех уравнений, следующих за тем, в котором эта неизвестная находится на главной диагонали. Например, неизвестную Т1 можно исключить из второго и третьего уравнений, а затем исключить Т2 из третьего уравнения. Чтобы исключить Т1 из второго и третьего уравнений, решим первое уравнение относительно Т1:
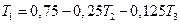
Подставив это выражение во второе уравнение, получим:
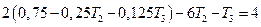
или
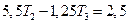
Подстановка в третье уравнение дает
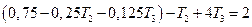
или
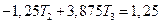
В результате система уравнений примет вид:
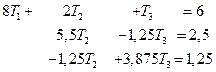 (2.49)
(2.49)
Повторим процедуру, исключая Т2 из третьего уравнения:
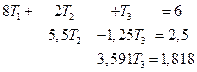 (2.50)
(2.50)
Эта система может быть решена обратной прогонкой. Из третьего уравнения получим:
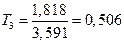
Подставляя это значение Т3 во второе уравнение, и решая его относительно Т2 получаем:
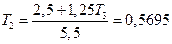
Поскольку Т2 и Т3 известны, из первого уравнения имеем
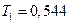
Мы видим, что метод включает два этапа. Первый состоит в превращении исходной матрицы в треугольную. На втором этапе решается полученная система уравнений. Первый этап обычно называют разложением матрицы, поскольку матрица жесткости переходит в более простую матрицу. Второй этап решения называют обратной прогонкой.
После того как мы подробно познакомились с методом, рассмотрим систему уравнений более общего вида. Снова предположим, что система уравнений симметрична и доминирующие члены находятся на главной диагонали. Кроме того, допустим, что матрица системы ленточного типа. Имея это в виду, рассмотрим приведенную ниже систему уравнений:
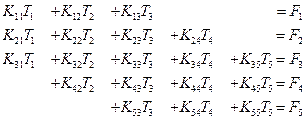 (2.51)
(2.51)
Ширина полосы матрицы, очевидно, равна трем. Нулевые коэффициенты здесь не показаны. После исключения Т1 имеем:
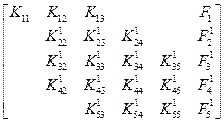 (2.52)
(2.52)
где коэффициенты расширенной 1) матрицы выражаются через исходные коэффициенты следующим образом:
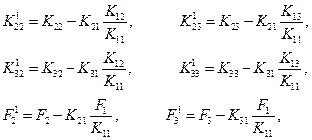
Верхний индекс (1) используется для обозначения первого исключения, или редукции. Общее соотношение для произвольного коэффициента после первой редукции имеет вид:
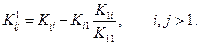
Редукции с номером n соответствует общее соотношение вида
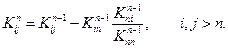 (2.53)
(2.53)
Аналогичные формулы получаются для вектор - столбца { F}:
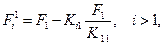
и
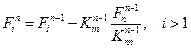 (2.54)
(2.54)
Из соотношения (2.53) можно извлечь важную информацию. Прежде всего очевидно, что симметрия в коэффициентах после операции исключения сохраняется. Это легко увидеть, сравнивая, например коэффициенты 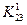 и
и 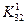 в матрице (2.52). Так как в исходной матрице К21=К12 и К13=К31, из вышеприведенных формул следует, что
в матрице (2.52). Так как в исходной матрице К21=К12 и К13=К31, из вышеприведенных формул следует, что 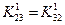 . Поскольку симметрия сохраняется после каждой редукции, то
. Поскольку симметрия сохраняется после каждой редукции, то 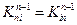 и матрица (2.50) может быть переписана в виде:
и матрица (2.50) может быть переписана в виде:
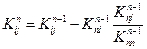 (2.55)
(2.55)
Разложение матрицы таким образом может быть проведено с использованием только коэффициентов, находящихся на главной диагонали и выше ее, так что нет необходимости запоминать полную матрицу.
Еще одну важную особенность можно обнаружить при рассмотрении матрицы (2.52); если 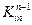 или
или 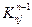 равно нулю, то
равно нулю, то 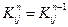 . Например, коэффициенты в четвертом и пятом столбцах и в четвертой и пятой строках матрицы (2.52) не изменилось после операции исключения, потому что
. Например, коэффициенты в четвертом и пятом столбцах и в четвертой и пятой строках матрицы (2.52) не изменилось после операции исключения, потому что 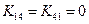 и
и 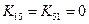 . На каждом шаге исключения следует рассматривать только те коэффициенты в пределах ширины полосы, которые изменяются в процессе исключения. Если система из 100 уравнений имеет матрицу с шириной полосы 15, только 15 уравнений этой системы видоизменяются после каждого отдельного исключения. Это приводит к экономии машинного времени при рассмотрении систем уравнений большого порядка.
. На каждом шаге исключения следует рассматривать только те коэффициенты в пределах ширины полосы, которые изменяются в процессе исключения. Если система из 100 уравнений имеет матрицу с шириной полосы 15, только 15 уравнений этой системы видоизменяются после каждого отдельного исключения. Это приводит к экономии машинного времени при рассмотрении систем уравнений большого порядка.
Элементы матрицы, находящиеся вне главной полосы, не влияют на процесс исключения (ибо они равны нулю). Следовательно, их помнить не нужно. Это обстоятельство позволяет хранить глобальную матрицу жесткости в виде прямоугольного массива шириной, равной ширине полосы матрицы.
Получающиеся после разложения коэффициенты 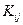 содержат достаточно информации, чтобы преобразовать надлежащим образом произвольный вектор столбец, даже если это не было сделано в процессе разложения матрицы. Последнее обстоятельство позволяет анализировать многочисленные вектор – столбцы {F} и дает определенное преимущество этому методу перед другими процедурами, которые применяются при рассмотрении отдельного вектор – столбца. Если {F} не модифицируется вместе с [K], рассматриваемый метод сводится к следующей трехшаговой процедуре:
содержат достаточно информации, чтобы преобразовать надлежащим образом произвольный вектор столбец, даже если это не было сделано в процессе разложения матрицы. Последнее обстоятельство позволяет анализировать многочисленные вектор – столбцы {F} и дает определенное преимущество этому методу перед другими процедурами, которые применяются при рассмотрении отдельного вектор – столбца. Если {F} не модифицируется вместе с [K], рассматриваемый метод сводится к следующей трехшаговой процедуре:
1. Матрица коэффициентов [K] преобразуется в верхнюю треугольную матрицу.
2. Вектор – столбец {F} модифицируется обращением n раз к формуле (2.54). Этот процесс называется прямым разложением.
3. Решение получается методом обратной прогонки.
Первый шаг обычно реализуется в одной подпрограмме, тогда как второй и третий шаги объединяются в другой подпрограмме.
Концепция метода конечных элементов
Метод конечных элементов основан на идее аппроксимации непрерывной функции (температуры, электрического потенциала, скорости, давления, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых элементами. Элементы в исследуемой области связаны между собой общими узловыми точками. В качестве функций элемента чаще всего применяется полином. Порядок полинома зависит от числа используемых в каждом узле элемента данных о непрерывной функции.
В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель можно построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. При построении дискретной модели непрерывной величины поступают следующим образом:
В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.
Значения непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.
Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.
Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границы элемента. Этот полином, связанный с каждым элементом назовем функцией элемента.
Основная концепция метода конечных элементов может быть наглядно проиллюстрирована на одномерном примере заданного распределения температуры в стержне, показанном на рис. 1.1. Рассматривается непрерывная величина 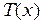 , область определения – отрезок
, область определения – отрезок 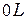 вдоль оси
вдоль оси 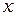 . Фиксированы и пронумерованы пять точек на оси
. Фиксированы и пронумерованы пять точек на оси 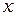 (см. рис. 1.2, а). Это узловые точки. Они могут быть расположены на разном расстоянии друг от друга. Количество узлов может быть произвольным. Значения
(см. рис. 1.2, а). Это узловые точки. Они могут быть расположены на разном расстоянии друг от друга. Количество узлов может быть произвольным. Значения 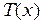 в данном случае известны в каждой узловой точке. Эти фиксированные значения представлены на рис. 1.2, б. и обозначены в соответствии с номерами узловых точек через
в данном случае известны в каждой узловой точке. Эти фиксированные значения представлены на рис. 1.2, б. и обозначены в соответствии с номерами узловых точек через 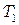 ,
, 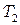 , …,
, …, 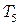 .
.
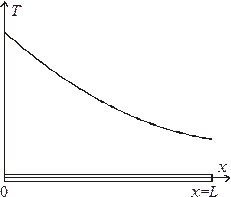 Рис. 1.1. Распределение температуры в одномерном стержне
Рис. 1.1. Распределение температуры в одномерном стержне
| 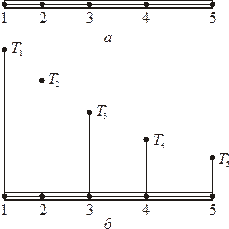 Рис. 1.2. Узловые точки и предполагаемые значения
Рис. 1.2. Узловые точки и предполагаемые значения 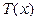
|
Разбиение области на элементы может быть проведена двумя различными способами. Можно, например, ограничить каждый элемент двумя соседними узловыми точками, образовав четыре элемента (см. рис. 1.3, а) или разбить область на два элемента, каждый из которых содержит три узла (см. рис. 1.3, б). Соответствующий элементу полином определяется по значениям 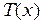 в узловых точках элемента. В случае разбиения области на четыре элемента, когда на каждый элемент приходится по два узла, функция элемента будет линейна по
в узловых точках элемента. В случае разбиения области на четыре элемента, когда на каждый элемент приходится по два узла, функция элемента будет линейна по 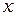 (две точки однозначно определяют прямую линию). Окончательная аппроксимация
(две точки однозначно определяют прямую линию). Окончательная аппроксимация 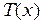 будет состоять из четырех кусочно-линейных функций, каждая из которых определена на отдельном элементе.
будет состоять из четырех кусочно-линейных функций, каждая из которых определена на отдельном элементе.
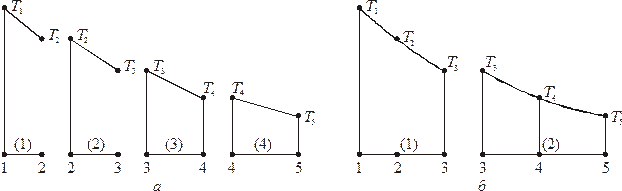
Рис. 1.3. Деление области на элементы
Другой способ разбиения области на два элемента с тремя узловыми точками приводит к представлению функции элемента в виде полинома второй степени. В этом случае окончательной аппроксимацией 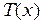 будет совокупность двух кусочно-непрерывных квадратичных функций. Отметим, что это приближение будет именно кусочно-непрерывным, так как углы наклона графиков обеих функций могут иметь разные значения в третьем узле.
будет совокупность двух кусочно-непрерывных квадратичных функций. Отметим, что это приближение будет именно кусочно-непрерывным, так как углы наклона графиков обеих функций могут иметь разные значения в третьем узле.
В общем случае распределение температуры неизвестно и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Снова определяются множество узлов и значения температуры в этих узлах 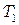 ,
, 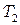 ,
, 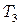 , …, которые теперь являются переменными, так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяются соответствующая функция элемента. Узловые значения
, …, которые теперь являются переменными, так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяются соответствующая функция элемента. Узловые значения 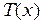 должны быть теперь подобраны таким образом, чтобы обеспечивалось «наилучшее» приближение к истинному распределению температуры. Этот подбор осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи, например, с помощью использования методов наименьших квадратов, метод Ритца, метод Галёркина или других [123–128]. В результате процесс минимизации задача сводится к решению системы линейных алгебраических уравнений относительно узловых значений
должны быть теперь подобраны таким образом, чтобы обеспечивалось «наилучшее» приближение к истинному распределению температуры. Этот подбор осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи, например, с помощью использования методов наименьших квадратов, метод Ритца, метод Галёркина или других [123–128]. В результате процесс минимизации задача сводится к решению системы линейных алгебраических уравнений относительно узловых значений 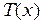 .
.
При построении дискретной модели непрерывной величины определенной в двух- или трехмерной области, основная концепция метода конечных элементов используется аналогично. В двухмерном случае элементы описываются функциями от 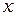 ,
, 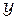 , при этом чаще всего рассматриваются элементы в форме треугольника или четырехугольника.
, при этом чаще всего рассматриваются элементы в форме треугольника или четырехугольника.
ДИСКРЕТИЗАЦИЯ ОБЛАСТИ
На первом этапе конечноэлементной процедуры производится разбиение расчетной области на конечные элементы. Этот этап не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся навыков. Плохое или несовершенное разбиение может приводить к ошибочным результатам.
Дискретизация области включает: выбор формы элементов; задание их размеров и их количество; нумерацию элементов и узлов.
Типы конечных элементов
Размерность элемента определяется размерностью аппроксимируемой их совокупностью области определения задачи. Для соответствия элемента физической модели исследуемого объекта одномерный элемент может иметь поперечное сечение, площадь которого необязательно постоянна по длине элемента, а двухмерный элемент единичную толщину.
Простейший конечный элемент имеет число узлов больше на единицу мерности элемента и называется симплекс-элемент. Конечный элемент, имеющий большее число узлов, называется комплекс-элементом.
На рис. 2.1 приведены симплекс-элементы различной размерности.

Рис. 2.1. Симплекс-элементы: а – одномерный;
б – двухмерный (треугольник); в – трехмерный (тетраэдр)
Симплекс-элементам соответствую полиномы, содержащие константу и линейные члены:
одномерный (см. рис. 2.1,а)
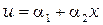 ; (2.1)
; (2.1)
двухмерный (см. рис. 2.1,б)
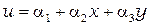 ; (2.2)
; (2.2)
трехмерный (см. рис. 2.1,в)
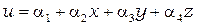 . (2.3)
. (2.3)
Нелинейные элементы высокого порядка, или комплекс-элементы должны иметь число узлов, равное числу коэффициентов в аппроксимирующем полиноме этого конечного элемента. Например, одномерный квадратичный элемент должен содержать три узла (см. рис. 2.2), т.к. его полином содержит три неизвестных коэффициента
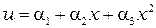 , (2.4)
, (2.4)
а кубический – четыре узла
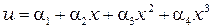 . (2.5)
. (2.5)
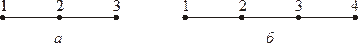
Рис. 2.2. Одномерные нелинейные элементы высокого порядка
а – квадратичный; б – кубический
Квадратичный треугольный элемент содержит шесть узлов (см. рис. 2.3), а полином – шесть коэффициентов
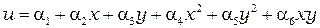 ; (2.6)
; (2.6)

Рис. 2.3. Квадратичный треугольный элемент
Нелинейный двухмерный элемент с наименьшим числом узлов – это четырехугольник (см. рис. 2.4)
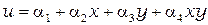 ; (2.7)
; (2.7)

Рис. 2.4. Нелинейный четырехугольный элемент
Одномерный симплекс-элемент
Одномерный симплекс-элемент представляет собой прямолинейный отрезок длины 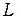 с двумя узлами, по одному, по одному на каждой стороне отрезка (см. рис. 2.5). Узлы обозначаются индексами
с двумя узлами, по одному, по одному на каждой стороне отрезка (см. рис. 2.5). Узлы обозначаются индексами 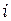 и
и 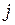 , узловые значения – через
, узловые значения – через 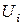 и
и 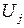 соответственно.
соответственно.
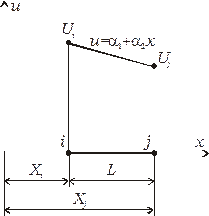
Рис. 2.5. Одномерный симплекс-элемент
Начало системы координат расположено вне элемента. Полиномиальная функция 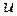 для скалярной величины имеет вид
для скалярной величины имеет вид
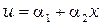 . (2.8)
. (2.8)
Здесь 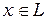 .
.
Коэффициенты полинома 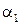 и
и 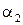 определяются через значения функции в узлах. В результате имеем систему из двух уравнений с двумя неизвестными
определяются через значения функции в узлах. В результате имеем систему из двух уравнений с двумя неизвестными
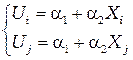 , (2.9)
, (2.9)
решение которой дает
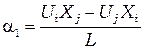 ,
, 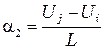 . (2.10)
. (2.10)
Подставляя найденные значения 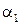 и
и 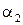 в формулу (2.8) получим
в формулу (2.8) получим
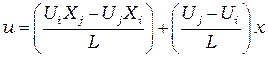 , (2.11)
, (2.11)
которое может быть переписано в виде
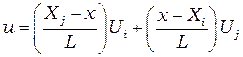 . (2.12)
. (2.12)
Линейные функции от 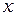 в формуле (2.12) называются функциями формы или интерполяционными функциями и обозначаются буквой
в формуле (2.12) называются функциями формы или интерполяционными функциями и обозначаются буквой 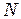
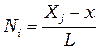 и
и 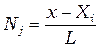 . (2.13)
. (2.13)
Как видно из формулы (2.13), функция 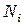 равна единице в узле с номером
равна единице в узле с номером 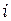 и равна нулю в узле
и равна нулю в узле 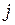 (см. рис. 2.6). Аналогично функция
(см. рис. 2.6). Аналогично функция 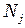 равна нулю в
равна нулю в 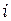 -м узле и равна единице в узле с номером
-м узле и равна единице в узле с номером 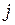 (см. рис. 2.6). Эти значения характерны для функций формы. Они равны единице в одном определенном узле и обращаются в нуль во всех других узлах.
(см. рис. 2.6). Эти значения характерны для функций формы. Они равны единице в одном определенном узле и обращаются в нуль во всех других узлах.

Рис. 2.6. Функции формы одномерного симплекс-элемента
Соотношение (2.12) может быть записано
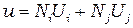 , (2.14)
, (2.14)
или в матричном виде
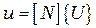 , (2.15)
, (2.15)
где 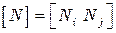 – матрица-строка функций формы конечного элемента (матрица функций формы);
– матрица-строка функций формы конечного элемента (матрица функций формы); 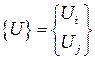 – вектор-столбец узловых значений функции
– вектор-столбец узловых значений функции 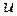 .
.
Выражение (2.15) является основополагающим и применимо к любым конечным элементам. Число элементов матриц 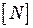 и
и 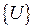 равно числу узлов конечного элемента. Для любой разновидности конечного элемента функция формы любого узла это функция заданная и непрерывная на конечном элементе и равная единице в этом узле и нулю во всех остальных узлах.
равно числу узлов конечного элемента. Для любой разновидности конечного элемента функция формы любого узла это функция заданная и непрерывная на конечном элементе и равная единице в этом узле и нулю во всех остальных узлах.
Двухмерный симплекс-элемент
Двухмерный симплекс-элемент показан на рис. 2.7.

Рис. 2.7. Двухмерный симплекс-элемент
В методе конечных элементов принята нумерация узлов против часовой стрелки, начиная от некоторого 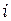 -го узла, который выбирается произвольно. Узловые значения скалярной величины
-го узла, который выбирается произвольно. Узловые значения скалярной величины 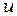 обозначаются через
обозначаются через 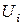 ,
, 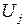 и
и 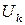 , а координатные пары трех узлов – через
, а координатные пары трех узлов – через 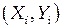 ,
, 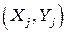 ,
, 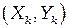 .
.
Интерполяционный полином имеет вид
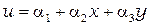 ; (2.16)
; (2.16)
Послед подстановки узловых значений функции 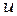 и соответствующих координат узлов получаем систему трёх уравнений
и соответствующих координат узлов получаем систему трёх уравнений
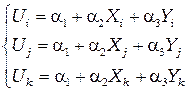 , (2.17)
, (2.17)
решая которую получаем
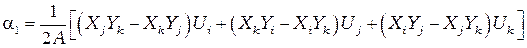 , (2.18)
, (2.18)
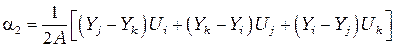 , (2.19)
, (2.19)
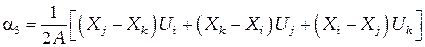 . (2.20)
. (2.20)
Определитель системы связан с площадью треугольника 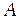 соотношением
соотношением
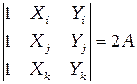 . (2.21)
. (2.21)
Выражения (2.18)–(2.20) можно записать в виде
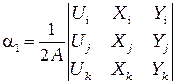 ,
, 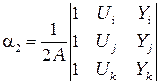 ,
, 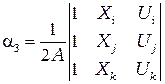
Подставляя значения 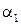 ,
, 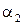 и
и 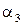 в формулу (2.16), можно преобразовать выражение для
в формулу (2.16), можно преобразовать выражение для 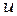 к виду, подобному (2.14). Это соотношение определяющее элемент, содержит три функции формы по одной для каждого узла:
к виду, подобному (2.14). Это соотношение определяющее элемент, содержит три функции формы по одной для каждого узла:
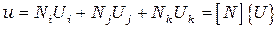 , (2.22)
, (2.22)
где 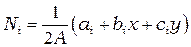 ;
; 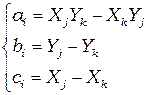 ; или
; или 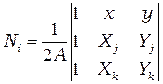 ;
;
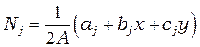 ;
; 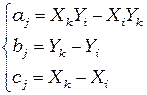 ; или
; или 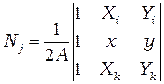 ;
;
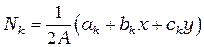 ;
; 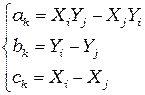 ; или
; или 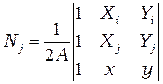 .
.
Значение функции формы 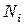 в
в 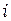 -м узле равно 1, а в узлах
-м узле равно 1, а в узлах 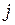 и
и 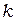 равно нулю. Аналогично функции
равно нулю. Аналогично функции 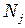 и
и 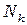 равны 1 соответственно в узлах
равны 1 соответственно в узлах 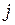 и
и 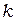 .
.
Скалярная величина 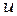 определяется внутри элемента функциями формы, линейными по
определяется внутри элемента функциями формы, линейными по 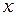 и
и 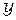 . Это означает, что градиенты этой величины в направлениях
. Это означает, что градиенты этой величины в направлениях 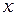 и
и 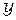 будут постоянны. Градиенты в направлении
будут постоянны. Градиенты в направлении 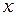 определяется соотношение
определяется соотношение
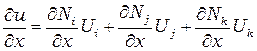 , (2.23)
, (2.23)
Поскольку
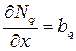 ,
, 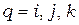 .
.
Поэтому
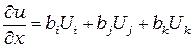 . (2.24)
. (2.24)
Так как 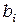 ,
, 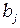 ,
, 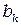 постоянны (они фиксированы как только заданы узловые координаты) и
постоянны (они фиксированы как только заданы узловые координаты) и 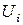 ,
, 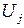 ,
, 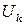 не зависят от координат пространства, частная производная в (2.24) имеет постоянное значение. Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию
не зависят от координат пространства, частная производная в (2.24) имеет постоянное значение. Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию 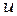 .
.
Дата: 2019-02-02, просмотров: 393.