Интерполяционный полином в общей форме имеет вид

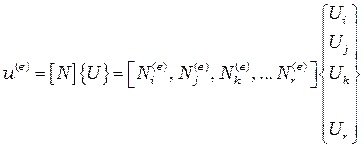                   .             (2.43)

где 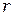 – число узлов элемента, верхний индекс  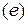означает произвольный элемент.

Техника включения элемента в область может быть проиллюстрирована на примере простой пятиэлементной конфигурации,  показанной на рис. 2.12 Узлы пронумерованы от единицы до шести. Величины 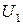, , 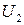, , 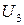,  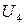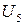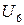представляют собой глобальные свободы. Координаты узлов 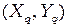, , 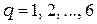известны. Номера элементов записаны в круглых скобках.

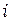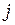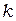Для обозначения номеров узлов элемента могут быть использованы принятые выше индексы ,  и , как только определен первый узел в каждом элементе. На рис. 2.12 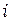-й узел в каждом элементе выделен звездочкой. Выбор этого узла совершенно произволен, хотя читатель вскоре сам убедится в удобстве именно такого расположения первых узлов. Узлы‚ м  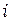и 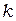 следуют за 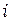-м узлом в направлении против часовой стрелки. Фиксирование узла  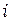позволяет записать следующие равенства для первого элемента:

, , .

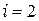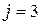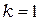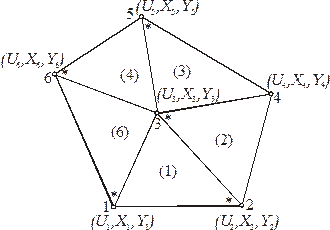
Рис. 2.13. Пятиэлементная область

Соответствие такого же типа может быть установлено для других элементов:

элемент 2: , , ,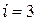

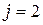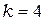элемент 3: , , ,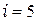

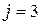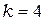элемент 4: , , ,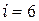

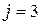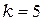элемент 5: , , ,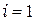

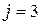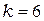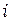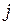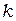С помощью этих соотношений можно осуществить включение элемента в область, так как они ставят в соответствие индексы элемента ,  и  глобальным номерам узлов. Этот процесс фиксирует координаты узлов элемента.

Значения индексов 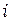,  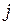и 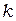 могут быть подставлены в формулу (2.43), что приводит к следующей совокупности уравнений для элементов

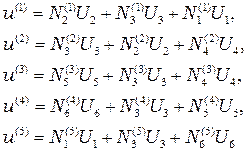                              ,                         (2.44)

Функции формы – множители при узловых значениях в формулах (2.44) – определяются подстановкой числовых значени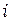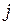й ,  и 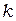 в уравнения для функций формы.

С помощью уравнений (2.44) достигается основная цель. Конечные элементы объединяются в ансамбль, а интерполяционные функции выражаются через глобальные узловые значения и глобальные координаты, которые вводятся вместо произвольных 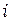,  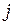и .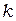

Каждое из уравнений в системе (2.44) содержит глобальные узловые значения, но относится к конкретному элементу. Мы будем а дальнейшем использовать расширенную форму этих уравнений, которая имеет вид

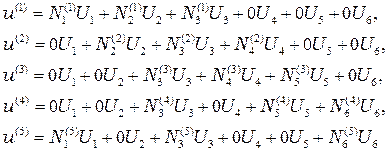                ,           (2.45)

Эти уравнения можно записать следующим образом:

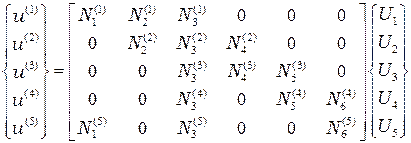              .        (2.46)

Сокращенная форма интерполяционных уравнений используется, когда осуществляется машинная реализация метода. Расширенная форма имеет некоторое преимущество, когда рассматривается процесс минимизации, который связан с дифференцированием матриц элементов.

2.7. Преобразование системы уравнений

Результирующая система уравнений имеет вид

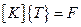                                                                                (2.47)

она получается суммированием уравнений для всех элементов. Эта система должна быть преобразована, если некоторые составляющие {T} известны, что является скорее правилом, чем исключением. В большинстве задач теории поля некоторые граничные значения искомой величины заданы; во всех задачах теории упругости должны быть фиксированы некоторые перемещения, с тем, чтобы исключить перемещение среды как жесткого тела. В задачах механики деформируемых сред матрица жесткости [K] будет сингулярной до тех пор, пока не заданы некоторые перемещения.

Цель этого раздела ­­– обсуждение и иллюстрация процедуры преобразования [K] и {F} таким образом, чтобы получить правильный ответ, не изменяя размеры [K] и {F}, ибо это повлечет за собой трудности при программировании.

Если фиксирована одна степень свободы узлового параметра {T}. То преобразование системы уравнений представляет собой двухшаговую процедуру. Пусть, например, известно значение Т5; преобразование сводится только к следующему:

1. Все коэффициенты пятой строки, за исключением диагональных, приравниваются нулю. Диагональный член остается неизменным. В форме равенства это выглядит как 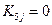 при j=1,…,n и 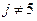. Соответствующая компонента F5 вектора {F} заменяется на произведение:

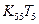
2. Все остальные уравнения преобразуются вычитанием произведения

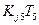
из F_j и подстановкой K_j5=0, j=1,…, n, j ≠5.

Пример

Требуется преобразовать следующую систему уравнений, если известно, что Т₁=150 и Т₅= 40:

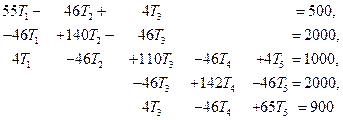
На первом этапе приравняем нулю все коэффициенты в первой и пятой строках, за исключением диагональных членов, которые оставим неизменными. Компоненты F ₁ и F ₅ в {F} заменим соответственно на K ₁₁ T ₁ и K ₅₅ T ₅. В результате будем иметь:

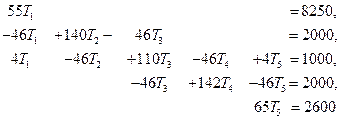
Второй этап состоит в исключении столбцов матрицы, коэффициенты которых умножаются на Т₁ и Т₅. Это осуществляется переносом членов, содержащих Т₁ и Т₅ в правую часть системы. Например, величина F₂ становится равной 2000+46Т₁, или 8900. Завершая второй шаг, получим:

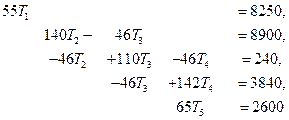
Описанная выше процедура совершенно проста и легко поддается программированию. Та же методика преобразования может быть использована также в случае, когда [K] хранится в виде прямоугольного массива. Логика программирования, однако, при этом более сложная.

Другой метод, применяемый некоторыми исследователями, состоит в том, что диагональный коэффициент, соответствующий заданному узловому значению Т _β, умножается на очень большое число, скажем на 10¹⁵, а F_β заменяется на (10¹⁵) Т _β. Это равносильно приближенной замене коэффициентов вне главной диагонали нулям. Такой способ очень легко реализовать на ЭВМ, но он неприменим, если значение Т _β очень мало. Именно с таким случаем сталкиваются при решении задач механики твердого деформируемого тела, когда заданные перемещения малы по величине. Первый метод, рассмотренный выше, всегда будет давать правильные результаты там, где мы сталкиваемся с малыми заданными величинами Т _β.

Решение системы уравнений

Одним из наиболее эффективных методов решения системы уравнений, которые получаются при использовании метода конечных элементов, является известный вариант метода исключения Гаусса. Матрица системы преобразуется к треугольному виду, после чего решение получается обратной прогонкой. Проиллюстрируем сначала метод на примере решения простой системы уравнений, а затем проведем обобщение, обсуждая вопросы, которые имеют отношение к методу конечных элементов.

Рассмотрим систему уравнений:

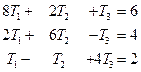                                                                    (2.48)

Матрица этой системы симметрична, причем наибольшие ее коэффициенты расположены на главной диагонали. Метод исключения основан на том, что любая неизвестная может быть исключена из всех уравнений, следующих за тем, в котором эта неизвестная находится на главной диагонали. Например, неизвестную Т₁ можно исключить из второго и третьего уравнений, а затем исключить Т₂ из третьего уравнения. Чтобы исключить Т₁ из второго и третьего уравнений, решим первое уравнение относительно Т₁:

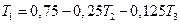
Подставив это выражение во второе уравнение, получим:

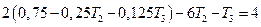
или

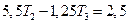
Подстановка в третье уравнение дает

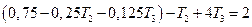
или

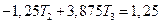
В результате система уравнений примет вид:

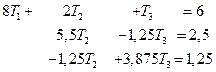                                   (2.49)

Повторим процедуру, исключая Т₂ из третьего уравнения:

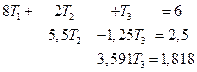                                        (2.50)

Эта система может быть решена обратной прогонкой. Из третьего уравнения получим:

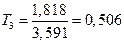
Подставляя это значение Т₃ во второе уравнение, и решая его относительно Т₂ получаем:

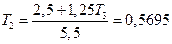
Поскольку Т₂ и Т₃ известны, из первого уравнения имеем

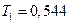
Мы видим, что метод включает два этапа. Первый состоит в превращении исходной матрицы в треугольную. На втором этапе решается полученная система уравнений. Первый этап обычно называют разложением матрицы, поскольку матрица жесткости переходит в более простую матрицу. Второй этап решения называют обратной прогонкой.

После того как мы подробно познакомились с методом, рассмотрим систему уравнений более общего вида. Снова предположим, что система уравнений симметрична и доминирующие члены находятся на главной диагонали. Кроме того, допустим, что матрица системы ленточного типа. Имея это в виду, рассмотрим приведенную ниже систему уравнений:

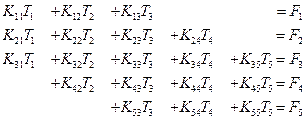                                  (2.51)

Ширина полосы матрицы, очевидно, равна трем. Нулевые коэффициенты здесь не показаны. После исключения Т₁ имеем:

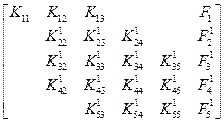                                                    (2.52)

где коэффициенты расширенной ¹⁾ матрицы выражаются через исходные коэффициенты следующим образом:

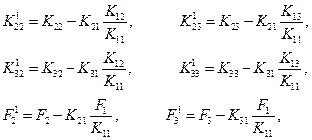
Верхний индекс (1) используется для обозначения первого исключения, или редукции. Общее соотношение для произвольного коэффициента после первой редукции имеет вид:

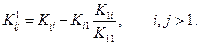
Редукции с номером n соответствует общее соотношение вида

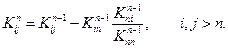                         (2.53)

Аналогичные формулы получаются для вектор - столбца { F}:

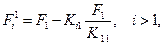
и

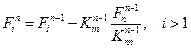                                                          (2.54)

Из соотношения (2.53) можно извлечь важную информацию. Прежде всего очевидно, что симметрия в коэффициентах после операции исключения сохраняется. Это легко увидеть, сравнивая, например коэффициенты 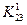 и 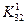 в матрице (2.52). Так как в исходной матрице К₂₁=К₁₂ и К₁₃=К₃₁, из вышеприведенных формул следует, что 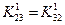. Поскольку симметрия сохраняется после каждой редукции, то  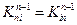и матрица (2.50) может быть переписана в виде:

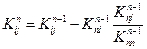                                                                  (2.55)

Разложение матрицы таким образом может быть проведено с использованием только коэффициентов, находящихся на главной диагонали и выше ее, так что нет необходимости запоминать полную матрицу.

Еще одну важную особенность можно обнаружить при рассмотрении матрицы (2.52); ес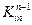ли  или 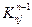 равно нулю, то 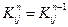. Например, коэффициенты в четвертом и пятом столбцах и в четвертой и пятой строках матрицы (2.52) не изменилось после операции исключения, потому что  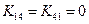и 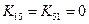. На каждом шаге исключения следует рассматривать только те коэффициенты в пределах ширины полосы, которые изменяются в процессе исключения. Если система из 100 уравнений имеет матрицу с шириной полосы 15, только 15 уравнений этой системы видоизменяются после каждого отдельного исключения. Это приводит к экономии машинного времени при рассмотрении систем уравнений большого порядка.

Элементы матрицы, находящиеся вне главной полосы, не влияют на процесс исключения (ибо они равны нулю). Следовательно, их помнить не нужно. Это обстоятельство позволяет хранить глобальную матрицу жесткости в виде прямоугольного массива шириной, равной ширине полосы матрицы.

Получающиеся после разложения коэффициенты 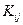 содержат достаточно информации, чтобы преобразовать надлежащим образом произвольный вектор столбец, даже если это не было сделано в процессе разложения матрицы. Последнее обстоятельство позволяет анализировать многочисленные вектор – столбцы {F} и дает определенное преимущество этому методу перед другими процедурами, которые применяются при рассмотрении отдельного вектор – столбца. Если {F} не модифицируется вместе с [K], рассматриваемый метод сводится к следующей трехшаговой процедуре:

1. Матрица коэффициентов [K] преобразуется в верхнюю треугольную матрицу.

2. Вектор – столбец {F} модифицируется обращением n раз к формуле (2.54). Этот процесс называется прямым разложением.

3. Решение получается методом обратной прогонки.

Первый шаг обычно реализуется в одной подпрограмме, тогда как второй и третий шаги объединяются в другой подпрограмме.