Имитационные модели принято классифицировать по четырем наиболее распространенным признакам:

типу используемой ЭВМ;

способу взаимодействия с пользователем;

способу управления системным временем (механизму системного времени);

способу организации квазипараллелизма (схеме формализации моделируемой системы).

Первые два признака позволяют разделить имитационные модели на совершенно понятные (очевидные) классы.

По типу используемой ЭВМ различают аналоговые, цифровые и гибридные имитационные модели. Достоинства и недостатки моделей каждого класса общеизвестны. В дальнейшем будем рассматривать только цифровые модели.

По способу взаимодействия с пользователем имитационные модели могут быть автоматическими (не требующими вмешательства исследователя после определения режима моделирования и задания исходных данных) и интерактивными (предусматривающими диалог с пользователем в том или ином режиме в соответствии со сценарием моделирования). Моделирование сложных систем, относящихся, как уже отмечалось, к классу эргатических систем, как правило, требует применения диалоговых моделей.

Различают два механизма системного времени:

задание времени с помощью постоянных временных интервалов (шагов);

задание времени с помощью переменных временных интервалов (моделирование по особым состояниям).

При реализации первого механизма системное время сдвигается на один и тот же интервал (шаг моделирования) независимо от того, какие события должны наступать в системе. При этом наступление всех событий, имевших место на очередном шаге, относят к его окончанию.

Рис.2.1, а содержит иллюстрацию данного механизма. Так, для этого механизма считают, что событие 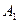 наступило в момент окончания первого шага; событие  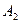- в момент окончания второго шага; события 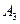, , 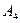 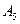- в момент окончания четвертого шага (эти моменты показаны стрелками) и т.д.

При моделировании по особым состояниям системное время каждый раз изменяется на величину, соответствующую интервалу времени до планируемого момента наступления следующего события, т.е. события обрабатываются поочередно - каждое «в свое время». Если в реальной системе какие-либо события наступают одновременно, это фиксируется в модели. Для реализации этого механизма требуется специальная процедура, в которой отслеживаются времена наступления всех событий и из них выделяется ближайшее по времени. Такую процедуру называют календарем событий.

На рис.2.1, б стрелками обозначены моменты изменения системного времени.

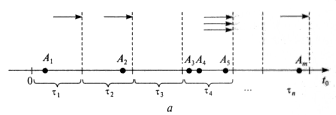
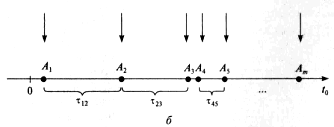
Рис.2.1. Реализация механизмов системного времени:

а) - с постоянным шагом; б) - с переменным шагом

Существует не столь распространенная разновидность механизма моделирования по особым состояниям, предусматривающая возможность изменения порядка обработки событий, так называемый механизм моделирования с реверсированием (обращением) шага по времени.

Согласно этому механизму, все события в системе разбиваются на два класса: фазовые и простые. К первым относят события, порядок моделирования которых нельзя изменять во избежание нарушения причинно-следственных связей в моделируемой системе. Остальные события относят к простым. Таким образом, сначала моделируют очередное фазовое событие, а затем все простые события до этого фазового, причем в произвольном порядке.

На рис.2.2 приведены перечисленные способы управления системным временем.

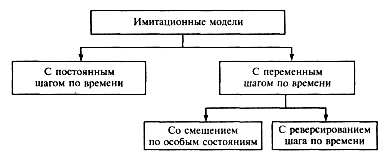
Рис.2.2. Механизмы управления системным временем

Очевидно, что механизм системного времени с постоянным шагом легко реализуем: достаточно менять временную координату на фиксированный шаг и проверять, какие события уже наступили.

Метод фиксированного шага целесообразно применять в следующих случаях:

события в системе появляются регулярно;

число событий велико;

все события являются для исследователя существенными (или заранее неизвестно, какие из них существенны).

Важнейшим классификационным признаком имитационных моделей является схема формализации моделируемой системы (способ организации квазипараллелизма).

Наибольшее распространение получили пять способов:

просмотр активностей;

составление расписания событий;

управление обслуживанием транзактов;

управление агрегатами; синхронизация процессов.

Характеристика этих способов требует введения ряда понятий.

Для задания свойств объектов используются атрибуты (параметры).

Совокупность объектов с одним и тем же набором атрибутов называют классом объектов. Все объекты делят на активные (представляющие в модели те объекты реальной системы, которые способны функционировать самостоятельно и выполнять некоторые действия над другими объектами) и пассивные (представляющие реальные объекты, самостоятельно в рамках данной модели не функционирующие).

Работа (активность) представляется в модели набором операторов, выполняемых в течение некоторого времени и приводящих к изменению состояний объектов системы. В рамках конкретной модели любая работа рассматривается как единый дискретный шаг (возможно, состоящий из других работ). Каждая работа характеризуется временем выполнения и потребляемыми ресурсами.

Событие представляет собой мгновенное изменение состояния некоторого объекта системы (т.е. изменение значений его атрибутов). Окончание любой активности в системе является событием, так как приводит к изменению состояния объекта (объектов), а также может служить инициатором другой работы в системе.

Под процессом понимают логически связанный набор активностей, относящихся к одному объекту. Выполнение таких активностей называют фазой процесса.

Различие между понятиями «активность» и «процесс» полностью определяется степенью детализации модели. Например, смена позиций мобильным объектом в одних моделях может рассматриваться как сложный процесс, а в других - как работа по изменению за некоторое время номера позиции.

Процессы, включающие одни и те же типы работ и событий, относят к одному классу. Таким образом, моделируемую систему можно представить соответствующим числом классов процессов. Между двумя последовательными фазами (работами) некоторого процесса может иметь место любое число фаз других процессов, а их чередование в модели, собственно, и выражает суть квазипараллелизма.

Способ просмотра активностей применяется при следующих условиях:

все ФД компонента реальной системы различны, причем для выполнения каждого из них требуется выполнение некоторых (своих) условий;

условия выполнимости известны исследователю заранее и могут быть заданы алгоритмически;

в результате ФД в системе наступают различные события;

связи между ФД отсутствуют, и они осуществляются независимо друг от друга.