Как и в предыдущем примере, допустим, что информация ограничена 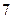 днями.

Рассчитаем средние значения и дисперсии для каждого дня прогнозного периода по формулам

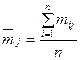;                                                                                         (2.15)

.                                                                              (2.16)

;

.

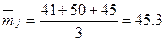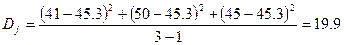Результаты расчетов приведены в таблице на рис.2.3.

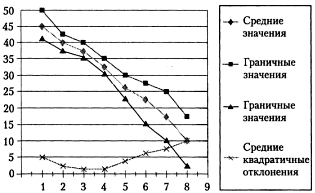
Рис.2.3. Зависимость средних значений и средних квадратических отклонений

от времени для трех реализаций

Для аппроксимации средних значений 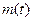 выберем линейную зависимость

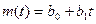.                                                                                     (2.17)

Таблица 2.5

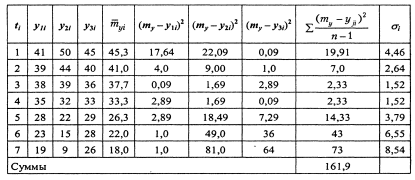
Воспользовавшись методом наименьших квадратов, найдем коэффициенты 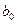 и .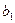

Спрогнозируем среднюю величину времени расхода запаса:

.

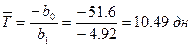Зависимост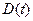и  и 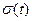 имеют явно нелинейный характер и для точных прогнозов они могут быть аппроксимированы полиномами различных порядков, например в виде параболы:

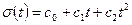                                                                             (2.18)

В первом приближении ограничимся средними значениями дисперсии и среднего квадратического отклонения 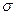, которое рассчитывается по формуле:

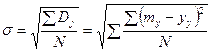.                                                            (2.19)

При подстановке значений из табл.2.5 находим:

.

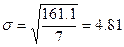Рассчитаем величину страхового запаса.

В первом случае расчет производится по формуле (2.5). Например, при 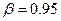 находим:

.

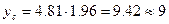Во втором случае расчет 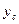 производится по формуле (2.6).

Особенность расчета для ансамбля реализаций состоит в том, что имеется возможность оценки величины 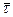 - среднего количества дней, в которые наблюдается дефицит деталей.

В общем случае 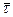 можно рассчитать по формуле:

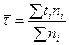,                                                                                            (2.20)

где 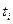 - число дней дефицита в 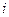-й реализации,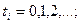  

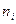 - количество 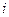-x реализаций.

Например, в рассматриваемом примере в первой реализации 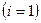 не наблюдается дефицита, т.е. 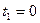; у второй  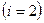- два дня дефицита 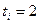; а у третьей  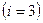нет дефицита.

Тогда по формуле (2.20):

.

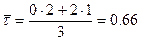При подстановке в (2.6) находим:

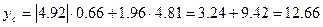
В заключение следует сделать следующие замечания:

1. Рассчитанные величины среднего запаса получены при условии, что наблюдающая величина дефицита и вариация ежедневного расхода - независимые величины. Несомненно, это допущение требует проверки.

2. При наличии большого количества реализаций расчет величины 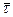 должен быть выполнен до проведения прогнозных расчетов.

Проверка формул (2.6) и (2.20) может быть осуществлена с использованием имитационного моделирования.

ИМИТАЦИОННЫЕ МОДЕЛИ ИНФОРМАЦИОННЫХ СИСТЕМ

Методологические основы применения метода

Имитационного моделирования

По Р.Шеннону ( Robert E.Shannon - профессор университета в Хантсвилле, штат Алабама, США), «имитационное моделирование - есть процесс конструирования на ЭВМ модели сложной реальной системы, функционирующей во времени, и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии, обеспечивающие функционирование данной системы».