Лекция №8 Методы прогнозирования в научных исследованиях и имитационное моделирование
Основные положения теории прогнозирования
Применение методов прогнозирования для решения прикладных задач
Имитационные модели информационных систем
Методологические основы применения метода имитационного моделирования
Классификация имитационных моделей
Основные положения теории прогнозирования
В снабженческой, производственной и транспортной сфере широко используются методы прогнозирования, поскольку значения прогнозных оценок развития анализируемых процессов или явлений являются основой принятия управленческих решений при оперативном, тактическом и стратегическом планировании.
Очевидно также, что точность и надежность прогноза определяет эффективность реализации различных операций и функций - от оценки вероятности дефицита продукции на складе до выбора стратегии развития фирмы.
Различным аспектам теории прогнозирования посвящено значительное количество исследований.
В большинстве работ по прогнозированию прогноз определяется как вероятностное научно обоснованное суждение о перспективах, возможных состояниях того или иного явления в будущем и (или) об альтернативных путях и сроках их осуществления.
Методологией прогнозирования - область знаний о методах, способах и системах прогнозирования.
Метод прогнозирования - способ исследования объекта, направленный на разработку прогноза.
Методика прогнозирования - совокупность одного или нескольких методов.
Система прогнозирования - упорядоченная совокупность методик и средств реализации.
Теория прогнозирования включает:
анализ объекта прогнозирования;
методы прогнозирования, подразделяющиеся на математические (формализованные) и экспертные (интуитивные);
системы прогнозирования.
При анализе объектов прогнозирования производится классификация прогнозов, при этом в качестве основных признаков указываются следующие:
масштабность, отражающая количество значащих переменных в описании объекта;
сложность, характеризующая степень взаимосвязи переменных;
детерминированность или стохастичность переменных;
информационная обеспеченность периода прогнозирования.
собственно период прогнозирования (краткосрочный прогноз - до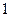 
года; среднесрочный - до 
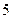лет; долгосрочный - свыше 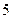лет.
Таблица 2.1
Динамика спроса в течение трех циклов расхода запасов
Й цикл
Й цикл
Й цикл
Проиллюстрируем возможные варианты прогнозов для одной реализации и для ансамбля из трех реализаций.
Закона распределения
| 
|
|
|
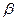
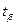
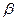
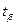
| 0,80 | 1,282 | 0,92 | 1,750 |
| 0,82 | 1,340 | 0,94 | 1,880 |
| 0,84 | 1,404 | 0,95 | 1,960 |
| 0,86 | 1,475 | 0,96 | 2,053 |
| 0,88 | 1,554 | 0,98 | 2,325 |
| 0,90 | 1,643 | 0,99 | 2,576 |
| 0,91 | 1,694 | 0,999 | 3,290 |
Для рассматриваемого примера для доверительной вероятности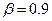 
по табл.2.3 находим 
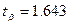и по формуле (2.5) величину страхового запаса:
.
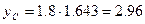Примем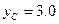 
.
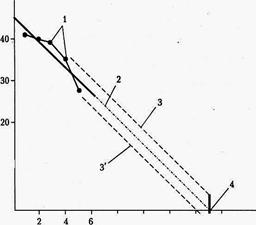
На рис.2.1 приведены границы интервального прогноза при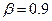 
.
У. ед.
Дни
Рис.2.1. Прогноз текущего расхода деталей на складе (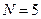 
):
1 - исходные данные; 2 - уравнение тренда; 3,3- границы
интервального прогноза; 4 - время расхода запаса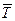 
Для учета возможных нарушений срока поставки необходимо оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой.
По одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки. Однако можно предположить, что выявленная тенденция расхода запаса, формула (1.2), сохранится.
В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой:
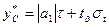, (2.6)
где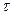 
- параметр, характеризующий количество дней задержки поставки заказа.
Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой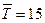 
дней, т.е. на 
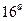день.
По формуле (2.6) находим:
.
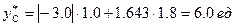Аналогично при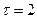 
( 
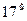день)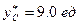 
.
Допустим, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения.
Определим вероятность отсутствия дефицита по формуле:
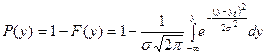, (2.7)
где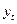 
- уравнение тренда, формула (2.1);
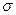- среднее квадратическое отклонение, формула (2.4).
Сделаем в интеграле замену переменной:
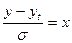(2.8)
и приведем его к виду:
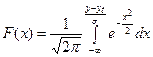. (2.9)
Для расчетов данного интеграла можно воспользоваться численными методами и ЭВМ или специальными таблицами.
Для нормальной функции распределения с параметрам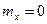и 
и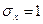 
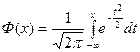. (2.10)
Очевидно, что: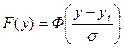 
.
В табл.2.4 приведен ряд значений функци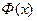и 
и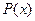 
.
Таблица 2.4
Имитационного моделирования
По Р.Шеннону ( Robert E.Shannon - профессор университета в Хантсвилле, штат Алабама, США), «имитационное моделирование - есть процесс конструирования на ЭВМ модели сложной реальной системы, функционирующей во времени, и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии, обеспечивающие функционирование данной системы».
Лекция №8 Методы прогнозирования в научных исследованиях и имитационное моделирование
Дата: 2019-02-02, просмотров: 302.
