Основные достоинства:

имитационная модель позволяет в принципе описать моделируемый процесс с большей адекватностью, чем другие;

имитационная модель обладает известной гибкостью варьирования структуры, алгоритмов и параметров системы;

применение ЭВМ существенно сокращает продолжительность испытаний по сравнению с натурным экспериментом (если он возможен), а также их стоимость.

Основные недостатки:

решение, полученное на имитационной модели, всегда носит частный характер, так как оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы;

большие трудозатраты на создание модели и проведение экспериментов, а также обработку их результатов;

если использование системы предполагает участие людей при проведении машинного эксперимента, на результаты может оказать влияние так называемый хауторнский эффект (заключающийся в том, что люди, зная (чувствуя), что за ними наблюдают, могут изменить свое обычное поведение).

Итак, само использование термина «имитационное моделирование» предполагает работу с такими ММ, с помощью которых результат исследуемой операции нельзя заранее вычислить или предсказать, поэтому необходим эксперимент (имитация) на модели при заданных исходных данных. В свою очередь, сущность машинной имитации заключается в реализации численного метода проведения на ЭВМ экспериментов с ММ, описывающими поведение сложной системы в течение заданного или формируемого периода времени.

Каждая имитационная модель представляет собой комбинацию шести основных составляющих: компонентов, параметров, переменных, функциональных зависимостей, ограничений, целевых функций.

Под компонентами понимают составные части, которые при соответствующем объединении образуют систему. Компоненты называют также элементами системы или ее подсистемами. Например, в модели рынка ценных бумаг компонентами могут выступать отделы коммерческого банка (кредитный, операционный и т.д.), ценные бумаги и их виды, доходы, котировка и т.п.

Параметры - это величины, которые исследователь (пользователь модели) может выбирать произвольно, т.е. управлять ими.

Переменные в отличие от параметров могут принимать только значения, определяемые видом данной функции.

Так, в выражении для плотности вероятности нормально распределенной случайной величины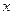

,

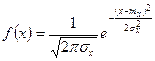где 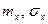- параметры;

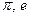 - константы;

х – переменная.

Различают экзогенные (являющиеся для модели входными и порождаемые вне системы) и эндогенные (возникающие в системе в результате воздействия внутренних причин) переменные. Эндогенные переменные иногда называют переменными состояния.

Функциональные зависимости описывают поведение параметров и переменных в пределах компонента или же выражают соотношения между компонентами системы. Эти соотношения могут быть либо детерминированными, либо стохастическими.

Ограничения - устанавливаемые пределы изменения значений переменных или ограничивающие условия их изменения. Они могут вводиться разработчиком (искусственные) или определяться самой системой вследствие присущих ей свойств (естественные).

Целевая функция предназначена для измерения степени достижения системой желаемой (требуемой) цели и вынесения оценочного суждения по результатам моделирования. Эту функцию также называют функцией критерия.

По сути, весь машинный эксперимент с имитационной моделью заключается в поиске таких стратегий управления системой, которые удовлетворяли бы одной из трех концепций ее рационального поведения: оптимизации, пригодности или адаптивизации.

При реализации имитационной модели, как правило, рассматриваются не все реально осуществляемые функциональные действия системы ( 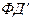), а только те из них, которые являются наиболее существенными для исследуемой операции. Кроме того, реальные  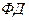аппроксимируются упрощенными действиями  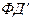причем степень этих упрощений определяется уровнем детализации учитываемых в модели факторов.

Названные обстоятельства порождают ошибки имитации процесса функционирования реальной системы, что, в свою очередь, обусловливает адекватность модели объекту-оригиналу и достоверность получаемых в ходе моделирования результатов.

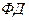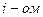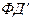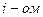На рис.1.1 схематично представлен пример выполнения некоторых  в  компоненте реальной системы и  в  компоненте ее модели.

В 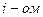 компоненте реальной системы последовательно выполняются 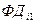, , 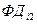,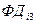… за время 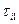, , 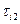,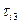… соответственно. На рисунке эти действия условно изображены пунктирными («непрямыми») стрелками. В результате ФД наступают соответствующие события: , , ,…

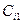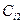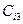В модели последовательность имитации иная: выполняется 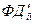 при неизменном времени, наступает модельное событие 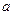, после чего время сдвигается на величину 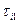, инициируя наступление события  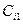и т.д.

Иными словами, модельной реализации упрощенных 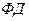 ( 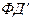) соответствует ломаная ( , , , , , , ,…).

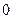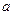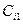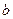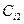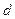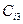Очевидно, что в реальной системе в различных се компонентах могут одновременно (параллельно) производиться функциональные действия и соответственно наступать события.

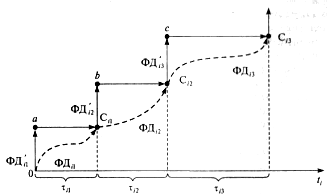
Рис.1.1. Моделирование функциональных действий в 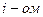 компоненте

В большинстве же современных ЭВМ в каждый из моментов времени можно отрабатывать лишь один алгоритм какого-либо 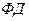. Возникает вопрос: каким образом учесть параллельность протекания процессов в реальной системе без потери существенной информации о ней?

Для обеспечения имитации наступления параллельных событий в реальной системе вводят специальную глобальную переменную 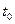, которую называют модельным (системным) временем. Именно с помощью этой переменной организуется синхронизация наступления всех событий в модели АИС и выполнение алгоритмов функционирования ее компонентов.