Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотрим применение методов прогнозирования на основе данных расхода деталей на складе. В табл.2.1 приведены три реализации текущего расхода. Для каждой реализации даны величины расхода за день и интегральные характеристики, представляющие собой расход деталей со склада за соответствующий цикл.

Таблица 2.1

Динамика спроса в течение трех циклов расхода запасов

Й цикл

Й цикл

Й цикл

день спрос, ед. всего с начала цикла день спрос, ед. всего с начала цикла день спрос, ед. всего с начала цикла 1 2 3 4 5 6 7 8 9 10 9 2 1 3 7 5 4 8 6 5 9 11 12 15 22 27 31 39 50 11 12 13 14 15 16 17 18 19 20 0 6 5 7 10 7 6 9 * * 0 6 11 18 28 35 41 50 50 50 21 22 23 24 25 26 27 28 29 30 5 5 4 3 4 1 2 8 3 4 5 10 14 17 21 22 24 32 35 39

Проиллюстрируем возможные варианты прогнозов для одной реализации и для ансамбля из трех реализаций.

Воспользуемся первой реализацией.

Допустим, что нам известны значения расхода деталей со склада за пять дней работы (табл.2.2).

Выберем уравнение тренда 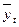 в виде линейной зависимости:

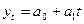.                                                                                        (2.1)

Расчет коэффициентов уравнения 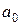 и 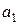 производится по формулам:

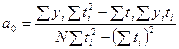;                                                                (2.2)

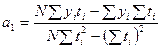.                                                                    (2.3)

Формулы (2.2) и (2.3) получены на основе метода наименьших квадратов.

Входящие в формулы значения сумм рассчитаны в табл.2.2. Подставляя их значения, находим

.

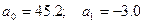Таким образом, уравнение прогноза пишется в виде:

.

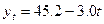Таблица 2.2

Исходные данные и результаты расчета коэффициентов

уравнения (2.1) при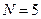

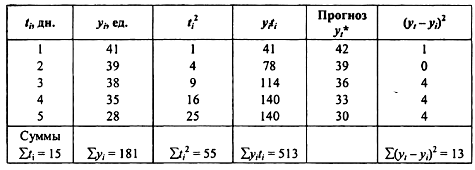
Для оценки границ интервального прогноза необходимо рассчитать среднее квадратичное отклонение:

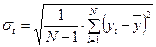.                                                                      (2.4)

Вспомогательные расчеты приведены в табл.2.2. Подставляя значения в формулу (2.4), находим :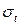

.

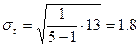На основании полученных зависимосте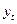й  и 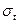 рассчитываются прогнозные оценки:

среднего времени расхода текущего запаса ;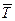

страхового запаса 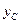 с заданной доверительной вероятностью ;

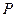вероятности отсутствия дефицита деталей на складе в течение прогнозируемого периода.

Приняв 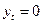, находим:

.

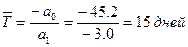Для расчета страхового запаса воспользуемся формулой:

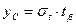,                                                                                          (2.5)

где 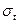 - среднее квадратичное отклонение, формула (2.4);

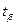 - параметр нормального закона распределения, соответствующий

доверительной вероятности .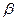

Параметр 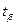 определяет для нормального закона число средних квадратических отклонений, которые нужно отложить от центра рассеивания (влево и вправо) для того, чтобы вероятность попадания в полученный участок была равна .

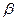В нашем случае доверительные интервалы откладывают вверх и вниз от среднего значения .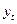

В табл.2.3 приведены наиболее часто встречающиеся в практических расчетах значения вероятности 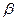 и параметра  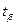для нормального закона распределения.

Таблица 2.3

Доверительная вероятность 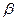 и параметр  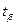нормального

Закона распределения

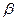
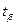
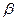
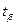
0,80	1,282	0,92	1,750
0,82	1,340	0,94	1,880
0,84	1,404	0,95	1,960
0,86	1,475	0,96	2,053
0,88	1,554	0,98	2,325
0,90	1,643	0,99	2,576
0,91	1,694	0,999	3,290

Для рассматриваемого примера для доверительной вероятности 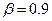 по табл.2.3 находим  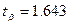и по формуле (2.5) величину страхового запаса:

.

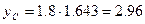Примем .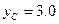

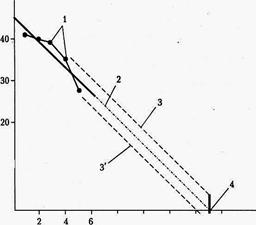
На рис.2.1 приведены границы интервального прогноза при .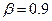

У. ед.

 Дни

Рис.2.1. Прогноз текущего расхода деталей на складе ( ):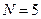

1 - исходные данные; 2 - уравнение тренда; 3,3- границы

интервального прогноза; 4 - время расхода запаса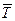

Для учета возможных нарушений срока поставки необходимо оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой.

По одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки. Однако можно предположить, что выявленная тенденция расхода запаса, формула (1.2), сохранится.

В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой:

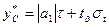,                                                                                 (2.6)

где 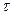 - параметр, характеризующий количество дней задержки поставки заказа.

Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой 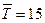 дней, т.е. на  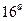день.

По формуле (2.6) находим:

.

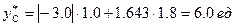Аналогично при 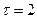 (  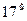день) .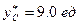

Допустим, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения.

Определим вероятность отсутствия дефицита по формуле:

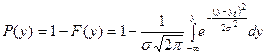,                                          (2.7)

где 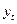 - уравнение тренда, формула (2.1);

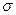 - среднее квадратическое отклонение, формула (2.4).

Сделаем в интеграле замену переменной:

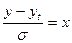                                                                                            (2.8)

и приведем его к виду:

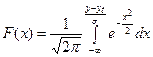.                                                                      (2.9)

Для расчетов данного интеграла можно воспользоваться численными методами и ЭВМ или специальными таблицами.

Для нормальной функции распределения с параметрам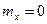и  и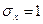

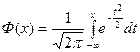.                                                                        (2.10)

Очевидно, что: .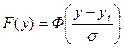

В табл.2.4 приведен ряд значений функци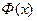и  и .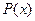

Таблица 2.4