1. Симплексные (простые) методы экстраполяции по временным рядам.

2. Статистические методы, включающие корреляционный и регрессионный анализ и др.

3. Комбинированные методы, представляющие собой синтез различных вариантов прогнозов.

При формировании методики прогнозирования целесообразно рассматривать прогноз в узком ( 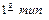 прогноза) и в широком смысле (  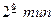прогноза).

В узком смысле прогноз выполняется при условии, что основные факторы, определяющие развитие прогнозируемого процесса или явления, не претерпят существенных изменений.

Прогнозы 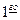 типа:

осуществляются с применением симплексных или статистических методов на основе временных рядов;

число значимых переменных включают от одного до трех параметров, т.е. по масштабности они относятся к сублокальным прогнозам;

при использовании одного параметра, например, времени, такие прогнозы считаются сверхпростыми, при двух-трех взаимосвязанных параметрах - сложными;

по степени информационной обеспеченности прогнозы этого типа могут быть отнесены к объектам с полным информационным обеспечением.

Прогноз 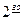 типа подразумевает, что исходные данные для получения оценок определяются с использованием опережающих методов прогнозирования: патентного, публикационного и др.

Как правило, прогнозы 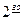 типа используются для долгосрочного прогнозирования и разбиваются на два этапа:

первый - получение прогнозных оценок основных факторов;

второй - собственно прогноз развития процесса или явления.

Наибольшее распространение получили методы прогнозирования 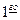 типа.

Наиболее часто для прогнозирования 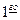 типа используется метод экстраполяции.

В общем случае модель прогноза включает три составляющие (рис.1.1) и записывается в виде:

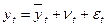,                                                                                    (1.1)

где 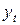 - прогнозные значения временного ряда;

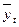 - среднее значение прогноза (тренд);

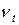 - составляющая, отражающая сезонные колебания (сезонная волна);

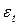 - случайная величина отклонения прогноза.

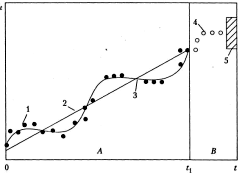
Рис.1.1. Прогнозирование на основе временных рядов:

1 - экспериментальные данные на интервале наблюдения (А);

2 - тренд; 3 - тренд и сезонная волна; 4 - значение точечного

прогноза на интервале упреждения (В); 5 - интервальный прогноз

При этом может быть предложена следующая последовательность расчета:

1. На основе значений временного ряда на предпрогнозном периоде (интервале наблюдения) с использованием метода наименьших квадратов определяются коэффициенты уравнения тренда 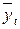, видом которого задаются.

Обычно для описания тренда используются полиномы различных порядков, экспоненциальные, степенные функции и т.п.

2. Для исследования сезонной волны значения тренда исключаются из исходного временного ряда. При наличии сезонной волны определяют коэффициенты уравнения, выбранного для аппроксимации .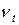

3. Случайные величины отклонения 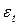 определяются после исключения из временного ряда значений тренда и сезонной волны на предпрогнозном периоде. Как правило, для описания случайной величины  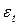используется нормальный закон распределения.

4. Для повышения точности прогноза применяются различные методы (дисконтирование, адаптация и др.). Наибольшее распространение в практике расчетов получил метод экспоненциального сглаживания, позволяющий повысить значимость последних уровней временного ряда по сравнению с начальными.